Roger Penrose is the recipient of the 2020 Nobel Prize in Physics "for his discovery that the formation of black holes is a reliable prediction of general relativity."
Also, the Nobel Prize in Physics was awarded to Reinhard Henzel and Andrea Gez "for the discovery of a supermassive compact object in the center of our galaxy."
Roger Penrose is a member of the Royal Society of London. He works in various fields of mathematics, general relativity and quantum theory. Penrose is the author of theories related to quantum consciousness, quantum leap, quantum biology, and the author of the book Fashion, Faith, Fantasy and the New Physics of the Universe, published by Peter Publishing House.
Fashion, Faith, Fantasy and the New Physics of the Universe is based on three lectures given by Penrose at Princeton University. The author himself admits that usually fashion, fantasy and faith do not bother people at all who seriously study the fundamental principles of the universe. We will leave faith to the churches, fashion to fashion shows, fantasy to writers. Roger Penrose proves in 500 pages that these romantic words can be important in the search for the foundation of the universe.
Fantasy
3.1. The Big Bang and the Friedman Universes
Could fantasy play any non-illusory role in our attempts to understand physical reality? Certainly fantasy is the complete opposite of science as such, and has no place in serious scientific discourse. However, the feeling remains that this issue is not as easy to dismiss as it might seem - many natural processes will seem fantastic, if we proceed from the conclusions that rational scientific experience based on reliable experimental research can lead us to. As we saw, especially in the previous chapter, the world is really arranged in the most fantastic way if we study it at the microlevel, where quantum phenomena reign. A specific material object can be in several places and, like a fabulous vampire (capable of transforming from a bat into a human and back again whenever he pleases),it can show either corpuscular or wave properties as if by its own choice. Moreover, his "behavior" obeys mysterious numbers, which contain the imaginary square root of -1.
Moreover, on an extremely large scale, phenomena are again being discovered, many of which may seem fantastic - perhaps even more striking than all the findings of literary fiction. For example, sometimes collisions are observed between entire galaxies, and one has to assume that they inevitably absorb each other (and we fix this by the arising distortions of space-time provoked by both galaxies).
Indeed, such distortions of space-time can sometimes be observed even directly - by the rough curvature of images of very distant galaxies. In addition, the most extreme space-time distortions known to us can lead to the emergence of massive black holes in outer space: we recently managed to observe how two such holes absorb each other and form an even larger one [Abbott et al., 2016]. There are black holes that are millions or tens of thousands of millions of times heavier than the Sun, so such holes could easily swallow entire solar systems. Nevertheless, these monsters are very small compared to the galaxies themselves, in the centers of which they are found. Often, such a black hole betrays its existence, generating two collimated beams of high-energy particles.These beams are expelled from the black hole in opposite directions from the tiny central region of the galaxy in which the hole sits; particles fly at a speed that can reach up to 99.5% of the speed of light [Tombesi et al., 2012; Piner, 2006]. Once we managed to observe how such a beam flew out of one galaxy and aimed at another, as if it were a colossal intergalactic war.
On an even larger scale, entire regions are discovered, filled with invisible something that permeates space. One gets the impression that this completely unknown substance accounts for about 84.5% of all matter in the universe. At the same time, there is something else that reaches the farthest limits of the observable Universe and seems to pull it apart in different directions with increasing speed. As if out of despair, scientists gave these two entities rather vague names - "dark matter" and "dark energy", respectively. It is dark matter and dark energy that mainly determine the overall structure of the known universe. The following fact seems even more alarming: modern cosmology almost certainly proves that the entire universe we know arose from one giant explosion,before which there was nothing at all - if at all it is possible to speak of something "before" the emergence of the space-time continuum, which, as we believe, underlies all material reality. Truly, such a Big Bang concept is a fantastic idea!
And there is; but we have at our disposal more and more empirical evidence in favor of the fact that at the dawn of existence, our universe was really incredibly dense and rapidly expanding. It contained not only all the material content of the cosmos that we know, but also all space-time, against the background of which the existence of physical reality is now being played out and which, apparently, stretches infinitely far in all directions. Everything we know appears to have come about as a result of this Big Bang. What is the evidence? We must assess the credibility of this idea and try to understand where it can lead us.
In this chapter, we will discuss some modern ideas about the origin of the universe itself, and in particular we will touch on the following problem: to what extent it is justified to resort to fantasy to explain empirical facts. In recent years, numerous experiments have indeed provided us with vast amounts of data that are directly relevant to understanding the origins of the universe. Things that previously seemed like a collection of mostly untested speculation have moved into the exact science category. Most important to mention are the satellites COBE, launched in 1989, WMAP, launched in 2001, and the Space Observatory. A plank that has been in operation since 2009. The aforementioned satellites gradually investigated the relict cosmic microwave background (see Section 3.4) in more and more detail. However, unresolved issues remain,and in search of answers to them, some specialists in theoretical cosmology went deep into the jungle, which is quite appropriate to call it absolutely fantastic.
Yes, to some extent, fantasy is certainly justified, but have modern theorists not rushed too zealously in this direction? In section 4.3, I will voice my own rather unconventional version to solve many of these mysteries. The ideas on which my answer is involved may also seem wild to some, and I will briefly describe why they should be taken seriously. Nevertheless, in this book I am more interested in the currently established ideas about the earliest stages of the evolution of our wonderful Universe, and I would like to discuss how plausible are certain directions in which some modern cosmologists are conducting their research.
To begin with, we have Einstein's majestic theory of general relativity, which is known to be extremely accurate in describing the structure of our curved spacetime and the motion of the heavenly bodies (see Sections 1.1 and 1.7). In 1922 and 1924, following Einstein's first attempts to apply this theory to describe the integral structure of the Universe, Russian mathematician Alexander Fridman first found solutions for Einstein's field equations in the context of a spatially uniform (homogeneous and isotropic) distribution of expanding matter, and an ideal liquid was considered an approximate model of such matter (dust solution) representing the average mass-energy distribution of galaxies [Rindler, 2001; Wald, 1984; Hartle, 2003; Weinberg, 1972]. Indeed, from an empirical point of view, it seemsthat in this case a fairly good general approximation to the average distribution of matter in the existing Universe is obtained, and the energy tensor is derivedT , which Friedman needed to represent gravity in the Einstein equation G = 8π ע T + Λg (see Section 1.1). A characteristic feature of Friedman's models is that the expansion begins with a singularity (now this moment is called the Big Bang). Then the curvature of space-time was infinite, and the mass-energy density of the source of matter T would rush to infinity if we tried to rewind time back to this space-time singularity.
(Surprisingly, the now commonly used term "Big Bang" was conceived as a pejorative; coined by Fred Hoyle, an ardent supporter of the alternative theory of a stationary universe; see Section 3.2.) He first mentioned the words "Big Bang" in a BBC radio made in 1950. Section 3.10 mentions these interviews in a different context; later, a book was compiled on their basis [Hoyle, 1950].
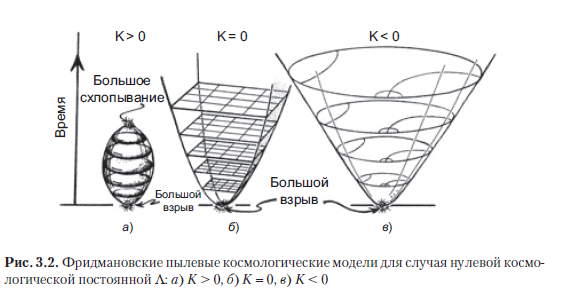
While I will conditionally assume that the very small Einstein cosmological constant Λ - it is this constant that determines the accelerating expansion of the Universe, mentioned earlier (see also Section 1.1) - is equal to zero. Then we need to consider only three separate situations determined by the spatial geometry: the curvature of the space K can be positive (K> 0), zero (K = 0) or negative (K <0). In authoritative books on cosmology, it is customary to normalize the value of K, bringing it to one of three values: 1, 0, –1. Here the story will be clearer if we consider K a real number that characterizes the actual curvature of space. We can think of K as a quantity indicating such spatial curvature at some specially selected time t. For example, you can agreethat t will correspond to the epoch of the last scattering (see Section 3.4), when the cosmic microwave background was formed, but the choice of a specific moment is not important in this case. The bottom line is that the sign of K will not change over time, therefore, a positive, negative or zero value of K characterizes the model as a whole, regardless of the chosen "reference point".
However, it should be noted that the value of K by itself does not fully characterize the geometry of space-time. There are also non-standard "folded" versions of such models, the spatial geometry of which is quite complex, and in some examples the Universe may be finite, even if K = 0 or K <0. Some scientists were interested in
such models (see Levin [2012], Luminet et al., [2003], originally Schwarzschild [1900]). However, these models are not important to us here; this problem does not significantly affect most of the arguments that I am presenting in this case. If we do not take into account the topological difficulties, then we get only three types of homogeneous geometry, which (on the plane) were very beautifully depicted by the Dutch artist M.K. Escher (Fig. 3.1; compare also with Fig. 1.38 in section 1.15). The 3D picture looks the same.
The easiest way to understand the case is K = 0, since in this case the spatial section will be an ordinary three-dimensional Euclidean space, although in order to describe the expanding Universe, we will need many such successive sections: see Fig. 3.2 b. (This expansion can be understood in terms of the diverging timelike lines that correspond to the world lines of the idealized galaxies described by this model. These will be the timelines, which we will talk about later.) Three-dimensional spaces, which are spatial sections in the case of K> 0, are a little more difficult to represent. since they are 3-spheres (), each of which in three dimensions is analogous to the two-dimensional surface of an ordinary sphere (), and the expansion of the Universe is expressed as an increase in the radius of the sphere with time (Fig. 3.2 a). In the case of negative curvature (K <0), three-dimensional spaces have a hyperbolic geometry (aka Lobachevsky geometry). Such geometry can be accurately represented using the conformal representation (Beltrami - Poincaré), which in the two-dimensional case is described as a region bounded by a circle S in the Euclidean plane, where straight lines are represented as circular arcs intersecting the bounding circle at right angles (Fig. 3.2 in and Figure 1.38 in section 1.15) (see, in particular, RQR, sections 2.4–2.6; Needham [1997]). Three-dimensional hyperbolic geometry looks similar, however, instead of a circle S, it contains a sphere (ordinary 2-sphere), which bounds a region (3-ball) in Euclidean three-dimensional space.
The term "conformal" used in these models is used because in hyperbolic geometry the angle between two smooth curves at their intersection point will be the same as in the background Euclidean geometry (for example, the angles at the tips of fish fins in Fig. 1.38a or the wings of the devils in Figure 3.1c are shown without distortion, no matter how close to the bounding circle they are). Another (rough) formulation of the same principle is that the shapes (but not dimensions) of very fine details in such representations are always displayed without distortion (see also Figure A.39 in Section A.10).
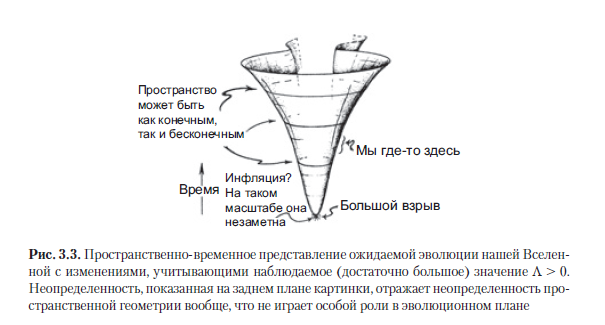
As noted earlier, some convincing evidence has already been found that in our Universe the cosmological constant Λ has a small positive value, so we must consider Friedmann models corresponding to Λ> 0. In fact, no matter how insignificant Λ is, its value is still sufficient is large (at the same time, according to Einstein's equations, we continue to consider it a constant) in order to overcome the collapse and “big collapse” shown in Fig. 3.2 a. Instead, with all three possible K values allowed by current observations, the universe should eventually expand with acceleration. With such a positive constant Λ, the expansion of the Universe will continue indefinitely and eventually become exponential (see Figure A.1 in Section A.1).According to such calculations, we imagine the general history of the Universe as shown in Fig. 3.3. The background is depicted vaguely to show that the observations allow for all three variations in the spatial curvature of K.
The variants of the distant future in all these models for Λ> 0, even with some irregularities in them, are very similar and are well described by a specific space-time model, which is called the de Sitter space. Einstein's tensor T in it is simply Λg . This model was found by Willem de Sitter (and independently by Tullio Levi-Civita) in 1917 (see [de Sitter, 1917a, b; Levi-Cività, 1917; Schrödinger, 1956]; PCR, p. 28.4). At present, it is generally accepted that this model well approximates the distant future of our Universe, when the energy tensor is completely determined by Λ, therefore, in the extremely distant future, the situation G≈Λg will develop .
Of course, here we assume that the Einstein equations (G = 8π ע T + Λg)will act indefinitely and the value of Λ, defined in our time, will remain constant. Section 3.9 will show that, according to the exotic ideas of inflationary cosmology, de Sitter's model should have described the Universe at a much earlier stage, immediately after the Big Bang, but the value of Λ at that time should have been colossally higher than the current one. These questions will become important for us later (see Sections 3.7-3.9 and 4.3), but for now we will not dwell on them in detail.
De Sitter space is a highly symmetric spacetime that can be described as a (pseudo-) sphere in five-dimensional Minkowski space (Fig. 3.4 a). This (pseudo-) sphere arises at the point = –3 / Λ, obtaining the local metric structure from the enclosing five-dimensional Minkowski space with coordinates (t, w, x, y, z) (Those who know how to write metrics in the standard way using differentials understand that this five-dimensional Minkowski metric takes the form =.) De-Sitter space completely repeats the symmetry of the four-dimensional Minkowski space; in both cases, we have a 10-parameter symmetry group. You can also recall the hypothetical anti-de-Sitter space discussed in section 1.15. It is very closely related to the de Sitter space and has a symmetry group of the same order.
De Sitter space is an empty model in which the energy tensor Tis zero, so there are no (idealized) galaxies that could define timelines, whose orthogonal three-dimensional spatial sections would allow one to define specific three-dimensional geometries of "synchronous time". In fact, a rather remarkable fact: it turns out that such three-dimensional spatial sections (with synchronous time) can be selected in de-Sitter space in three fundamentally different ways, so that de-Sitter space can be interpreted as a universe uniformly expanding in space with each of three alternative types of spatial curvature, depending on how it is cut by such three-dimensional sections corresponding to the same cosmic time: K> 0 (at t = const), K = 0 (at t - w = const) and K <0 ( at –w = const) (Fig. 3.4 b – d).This was beautifully demonstrated by Erwin Schrödinger in his book Expanding Universes (1956). An earlier model of a stationary universe, which we will discuss in Section 3.2, is described by the de Sitter space in accordance with the K = 0 cross section shown in Fig. 3.4 c (and conformally shown in Fig. 3.26 b in Section 3.5). Most versions of inflationary cosmology (which we will get to in Section 3.9) also use such a cut K = 0, so inflation can continue uniformly and exponentially for an unlimited time.26 b in Section 3.5). Most versions of inflationary cosmology (which we will get to in Section 3.9) also use such a cut K = 0, so inflation can continue uniformly and exponentially for an unlimited time.26 b in Section 3.5). Most versions of inflationary cosmology (which we will reach in Section 3.9) also use such a cut K = 0, so inflation can continue uniformly and exponentially for an unlimited time.
In fact, with regard to the large-scale structure of our real Universe, modern observations do not allow us to unequivocally answer which of these variants of spatial geometry most accurately describes it. Nevertheless, whatever the final answer may be, it does not now seem that the K = 0 option is that close to the truth (noteworthy, especially given the seemingly compelling evidence in favor of K <0 that emerged towards the end of the 20th century). In a sense, this situation is extremely unsatisfactory from an empirical point of view; for if we can only say that the value of K is very close to zero, then there is still the possibility that more careful observation (or a more convincing theory) will subsequently show thatthat our Universe corresponds more precisely to some other spatial geometry (that is, spherical or hyperbolic). So, if in the end there is good evidence in favor of K> 0, this will be truly important from a philosophical point of view, since it would mean that the spatial dimensions of the universe are finite. However, as of now, it is customary to simply state the following: according to observations, K = 0. This may be a very good approximation, but in any case we do not know how close the real universe is to true spatial homogeneity and isotropy, especially given certain conflicting data. obtained by observing the cosmic microwave background (eg, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).if in the end there is good evidence in favor of K> 0, this will be truly important from a philosophical point of view, since it would mean that the spatial dimensions of the universe are finite. However, as of now, it is customary to simply state the following: according to observations, K = 0. This may be a very good approximation, but in any case we do not know how close the real universe is to true spatial homogeneity and isotropy, especially given certain conflicting data. obtained by observing the cosmic microwave background (eg, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).if in the end there is good evidence in favor of K> 0, this will be truly important from a philosophical point of view, since it would mean that the spatial dimensions of the universe are finite. However, as of now, it is customary to simply state the following: according to observations, K = 0. This may be a very good approximation, but in any case we do not know how close the real universe is to true spatial homogeneity and isotropy, especially given certain conflicting data. obtained by observing the cosmic microwave background (eg, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).However, as of now, it is customary to simply state the following: according to observations, K = 0. This may be a very good approximation, but in any case we do not know how close the real universe is to true spatial homogeneity and isotropy, especially given certain conflicting data. obtained by observing the cosmic microwave background (eg, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).However, as of now, it is customary to simply state the following: according to observations, K = 0. This may be a very good approximation, but in any case, we do not know how close the real universe is to true spatial homogeneity and isotropy, especially given certain conflicting data. obtained by observing the cosmic microwave background (eg, [Starkman et al., 2012; Gurzadyan and Penrose, 2013, 2016]).
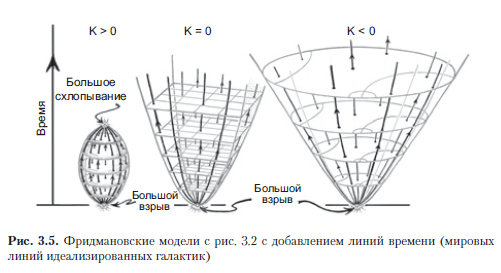
In order to build a picture of the complete space-time in accordance with Friedmann's models and their generalizations, you need to know how the “dimensions” of our spatial geometry will change over time, and from the very beginning. In standard cosmological models, for example, by Friedman, or in generalized models, briefly called FLRU (Friedman - Lemaitre - Robertson - Walker), in all models of this general class the spatial sections are homogeneous and isotropic and the total space-time has the same symmetry as and the sections themselves. They have a clear definition of cosmic time t, which describes the evolution of such a universal model. This cosmic time starts at the moment t = 0 (Big Bang) and is counted by idealized clocks following the world lines of idealized galaxies (Fig. 3.5, as well as Fig. 1.17 in section 1.7). I will refer to these world lines as time lines in the FLRU model (in cosmological works they are also sometimes called world lines of fundamental observers). Timelines are geodesic curves orthogonal to spatial sections, which, in turn, are 3-planes with the same t value.
The case of de Sitter space has an important feature: since, as mentioned earlier, the space is empty, that is, the energy-momentum tensor T in the equation G = 8πT + Λg is equal to zero, then we do not have any world lines associated with material bodies, which allowed would we define time lines or, respectively, spatial geometry. Therefore, locally we have a choice of how to interpret this model of describing the Universe: whether it corresponds to K> 0, K = 0, or K <0. Nevertheless, globally, these three situations differ, which can be seen in Fig. 3.4 b – d: in each of these cases, the slicing captures a different part of the integral de-Sitter space. Further
I will proceed from the fact that T is not equal to zero and provides a positive energy density of matter, which makes it possible to well determine both the time lines and spacelike 3-surfaces of constant time for each value of t, as shown in Fig. 3.2.
In the case with a positive curvature of space (K> 0) in the standard Friedman Universe filled with dust, its “size” can be characterized using the radius R of 3-spherical spatial sections, and this size can be studied as a function of t. At Λ = 0, we find the function R (t) describing the cycloid in the plane (R, t) (in this case, the speed of light is taken as a unit: c = 1). A cycloid is a curve with a simple geometric characteristic: it is described by a point of a circle rolling along the t axis (Fig. 3.6 b). Note that (after the time) the value of R again reaches zero, as in the Big Bang, therefore the entire model of the Universe with 0 <t < collapses again into a singularity, and this moment is often called a big collapse.
In the remaining cases K <0 and K = 0 (with zero Λ), the Universe will expand infinitely and there will be no large collapse. In the case K <0, there is a “radius” similar to R, but for K = 0, you can simply choose an arbitrary pair of world lines of idealized galaxies and take as R the segment dividing them in space. In the case K = 0, the expansion rate tends asymptotically to zero, and in the case K <0 - to some positive value.
Modern observations indicate that Λ is most likely positive and its value is sufficient to play a decisive role in the rate of expansion of the Universe, therefore the value of K loses its importance for this dynamics, and the Universe ultimately breaks down into accelerated expansion, as shown in fig. 3.3.
At the dawn of relativistic cosmology, a model with a positive K value (and Λ = 0) was often referred to as an oscillating model (Fig. 3.6 a), since the cycloid curve will continue indefinitely if we allow the "hoop" to make more than one revolution (dashed curve in Fig. 3.6 b ). It can be assumed that continuously replacing sections of the cycloid may correspond to successive cycles in the history of the real Universe, where, under the influence of some kind of shake-up, each collapse that the Universe undergoes is replaced by a new Big Bang. A similar possibility also arises at K = 0, and it can be assumed that at an earlier stage, space-time underwent a collapse, identical to the reversal of time at the stage of expansion, and the Big Collapse of that stage coincides with the Big Bang, which we consider the beginning of the current expansion of the Universe.Again, you would have to imagine some kind of bounce that somehow allows you to turn the implosion into an extension.
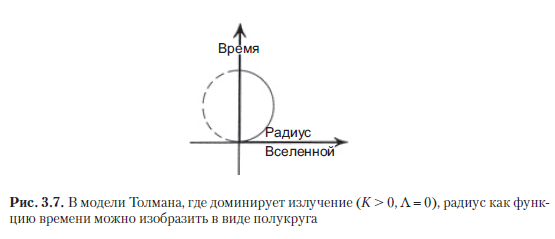
However, for such a picture to become physically plausible, it is required to present some convincing mathematical scheme that would be in agreement with modern physical concepts and methods and into which such a rebound would fit. For example, suppose you can change the equations of state that Friedman has adopted, with which he tried to describe the general distribution of matter in his "evenly smeared" galaxies. Friedman used an approximate model sometimes called a dust model; this model does not take into account any interactions (except for gravity) between "constituent elements" (ie "galaxies"), whose world lines are time lines. If we change the equations of state, this can significantly affect the properties of R (t) near t = 0. An even more accurate approximation,rather than Friedman's dust (in the period immediately after the Big Bang), such an equation of state appears, which was later used by Richard Chase Tolman [1934], an American specialist in mathematical physics and cosmology. In Tolman's FLRU models, the equation of state of pure radiation was used. It is believed that it is a good approximation of the state of matter at the earliest stages of the development of the Universe, when it was so hot that each particle had much more energy than the equationthat it well approximates the state of matter at the earliest stages of the development of the Universe, when it was so hot that each particle had significantly more energy than according to the equationthat it well approximates the state of matter at the earliest stages of the development of the Universe, when it was so hot that each particle had significantly more energy than according to the equationfor the mass m of even the heaviest particles that could exist immediately after the Big Bang. In Tolman's scheme for the case K> 0, the curve R (t) is not an arc of the cycloid, but (with a properly selected scale R and t) forms a semicircle (Fig. 3.7). In the case of the dust model, it would be possible to justify the transition from Collapse to Explosion by resorting to an analytic continuation (see Section A.10), which indeed allows one to pass from one arc of the cycloid curve to the next in such a mathematical way. But in Tolman's model with pure radiation, the analytic continuation would simply complement the semicircle and turn it into a circle, and this does not make any sense if this procedure is of interest to us for describing a bounce, that is, it should allow a continuation towards negative values of t.
For the new equation of state to describe the rebound mechanism, something much more radical than Tolman radiation is needed. In this case, such a serious point deserves attention: if a rebound occurs at some nonsingular transition, during which the smoothness of space-time and the spatial symmetry of the model are preserved, then the converging time lines of the compression phase can turn into diverging time lines of the expansion phase, passing through the bottleneck ”That would combine both of these phases. If this neck were smooth (nonsingular), then the transformation of such an extreme convergence of time lines into an extreme divergence would be achievable with an incredible curvature of the neck, which would lead to strong repulsion, and this grossly contradicts the standard conditions for positive energy,which is satisfied by ordinary classical matter (see sections 1.11, 3.2 and 3.7; [Hawking and Penrose, 1970]).
Therefore, one cannot expect that any reasonable classical equation of state would allow us to describe the rebound in the context of FLRU models, and the question inevitably arises: would not the equations of quantum mechanics help us move in this direction? It is necessary to take into account that near the classical FLRU-singularity, the curvature of space-time becomes indefinitely large. If we tried to describe such curvature in terms of its radius, then this radius (the inverse of the curvature) would be correspondingly small. Continuing to adhere to the concepts of classical geometry, as we approach the classical singularity, we would receive ever smaller radii of curvature of space-time, and as a result, the radius would become even less than the Planck scale of the order
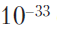see (see sections 1.1 and 1.5). Most theorists, thinking about quantum gravity, assume that at these scales, spacetime would already be sharply different from its usual form (smooth manifold) (although in Section 4.3 I will put forward completely different arguments on this score). Whether it is true or not, there is no reason to doubt that the procedures of general relativity will inevitably have to be modified so that they are combined with the methods of quantum mechanics on the approaches to such a radically curved space-time geometry. That is, we need a theory of quantum gravity suitable for our case, which would allow us to cope with situations in which classical Einstein procedures lead to a singularity (but compare with Section 4.3).
We often hear statements that such a precedent has already happened. As noted in Section 2.1, at the beginning of the 20th century, a serious problem arose with the classical concepts of the atom, since, according to the theory, the atoms should have catastrophically collapsed into a singular state, when electrons would spirally fall onto the nucleus (with the generation of a radiation pulse), and solve this problem was only possible with the advent of quantum mechanics. Shouldn't one expect that even when discussing such a catastrophic collapse of the entire Universe, the situation could become clearer at the level of quantum mechanics? But here's the catch: even now, there is no generally accepted hypothesis of quantum gravity. Even more serious is the fact that most of the hypotheses already put forward do not solve the singularity problem - singularities remain even in a quantized theory.There are some noteworthy exceptions - the nonsingular quantum bounce hypothesis [Bojowald, 2007; Ashtekar et al., 2006], but I will have to return to this topic in Sections 3.9 and 3.11 (as well as in Section 4.3), where I argue that such hypotheses do not really give much hope for solving the singularity problem in our Universe. ...
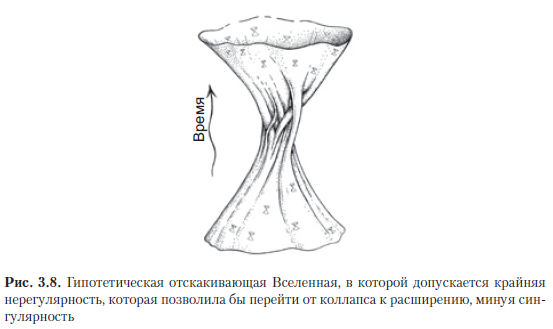
A completely different possibility of avoiding the singularity is associated with the expectation that small deviations from exact symmetry present at the stage of the collapse of the Universe could grow radically as the Big Implosion approaches, therefore, immediately before the complete collapse, the structure of space-time would not exactly correspond to the FLRU model. Therefore, the hope is often voiced that the singularity that manifests itself in FLRU-models may be false and that in a more general asymmetric situation, such classical space-time singularities simply will not arise; therefore, there is reason to expect that, in the general case, the collapsing Universe, due to some complex intermediate space-time geometry (Fig. 3.8), may turn to irregular expansion.Even Einstein himself tried to put forward such arguments - that the singularity can be avoided by rebounding from an irregular collapse [Einstein, 1931; Einstein and Rosen, 1935] or because the final collapse and singularities can somehow prevent the orbital motions of celestial bodies [Einstein, 1939].
It can be argued that after such an almost singular (but not strictly singular) collapse, a state will arise, the disturbances of which will gradually smooth out, and as a result it will strongly resemble the expanding FLRU model (as in Fig. 3.8). In 1963, this problem was analyzed in detail by two Soviet theoretical physicists - Evgeny Mikhailovich Lifshits and Isaak Markovich Khalatnikov [Lifshits and Khalatnikov, 1963]. Their work shows that, under normal conditions, such singularities apparently do not arise, which supports the hypothesis of nonsingular rebound described above. Accordingly, it was argued that in general relativity, space-time singularities that arise during gravitational collapse and appear in the known exact solutions of collapsing Friedmann models or other FLRU models are generated only becausethat known solutions have unrealistic specific properties, for example, strict symmetry. Therefore, such singularities would not have developed under the conditions of typical asymmetric perturbations. However, this assumption was not confirmed, which will be discussed in the next section.
»More details about the book can be found on the website of the publishing house
» Table of Contents
» Excerpt
For Habitants a 30% discount on coupon - Penrose
Upon payment for the paper version of the book, an e-book is sent to the e-mail.