At the mention of the phrase "sea sponge", someone may have an image of an extremely popular cartoon character in their head. However, the best employee Krusty Krab has nothing to do with his real prototype. Visually, different types of sea sponges look different: ancient Greek amphorae, intricate wind instruments, dried tree branches, fancy flowers, etc. But behind the external appearance is an incredibly complex cellular structure that has attracted the attention of the scientific community for several years now. Researchers at Harvard University recently found that the structural features of sea sponges can serve as inspiration for stronger and taller skyscrapers, longer bridges and ultralight spaceships. Why is the structure of the sea sponge unique,what are its mechanical characteristics, and what results did prototypes based on the obtained data show? We will find answers to these questions in the report of scientists. Go.
Research basis
There are about 8000 species of sea sponges in the world, but this study focuses on the six-rayed sponges ( Hexactinellida ). This type of sponge is also very diverse, with about 600 species. They live in the seas at depths from 5 to more than 6000 meters.
The six-rayed sponges got their name from the structure of their skeleton, which consists of six-rayed silicon needles, which are located in three mutually perpendicular planes.
The body shape of Hexactinellida can be very different: tubular, goblet, lumpy, processous, lobed, etc. Despite the visual differences, the body composition of all species is quite similar. The basis of the body is a single syncytium * .
* — , .A diagram alone is enough to understand why a glass sponge can be so useful in architecture or bridge construction.
(Hexactinellida): — ; - — ; — ; — .
In this study, scientists examined the mineralized skeletal system of the Euplectella aspergillum sponge (Venus flower basket), which has a unique hierarchical architecture and mechanical strength on many length scales.

Euplectella aspergillum (top view).
Vitreous skeletal elements (spicules) E. aspergillum comprised of a central protein core surrounded by alternating concentric layers of consolidated silica nanoparticles (silica, SiO 2) and thin organic layers. The spicules are organized to form a square grid, reinforced by two intersecting sets of paired diagonal struts, creating a checkerboard-like pattern of alternating open and closed cells.
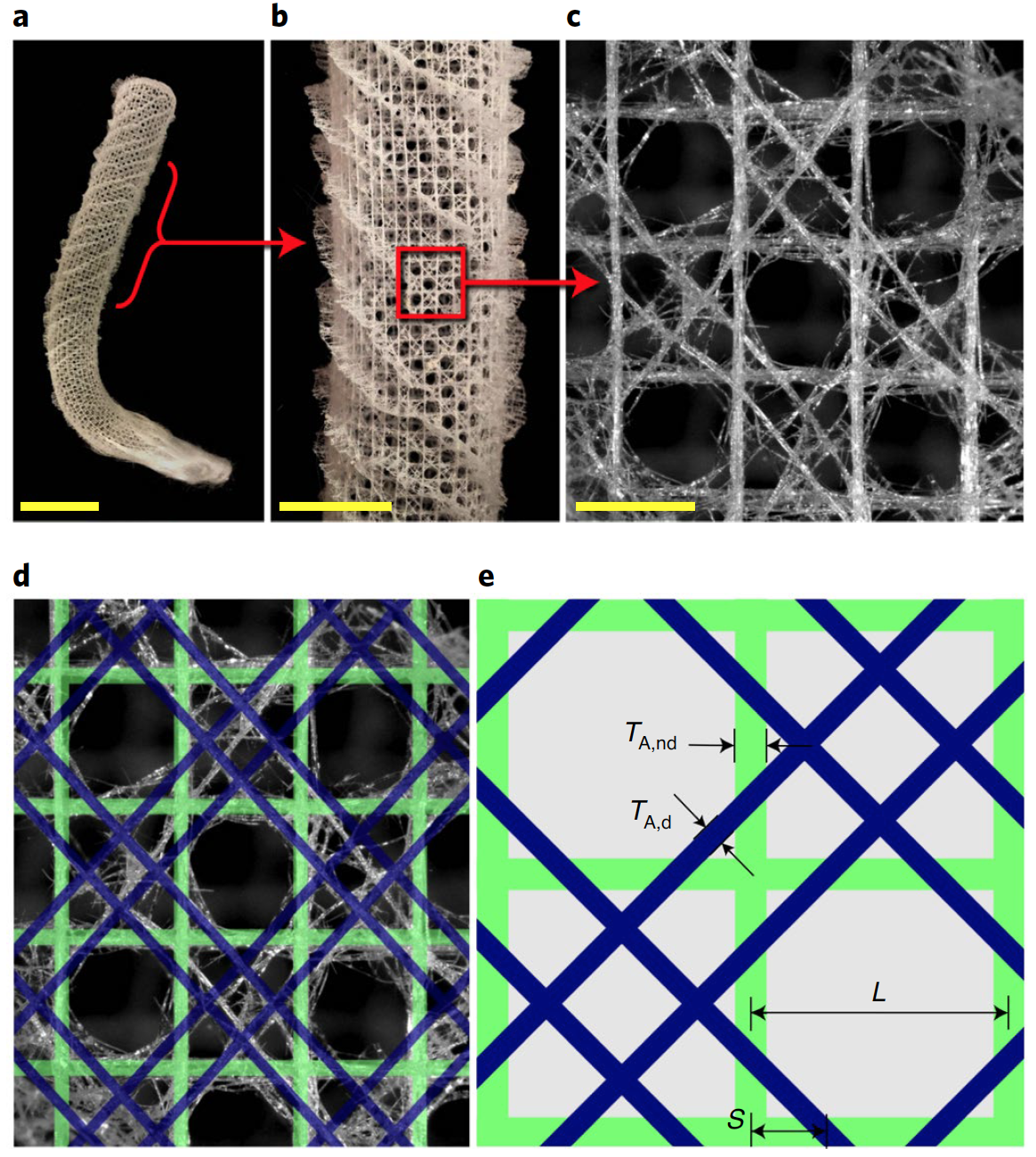
Image # 1
Previously, the effect of multilayer spicule architecture on slowing crack propagation and on increasing flexural strength has been considered, but the potential mechanical advantages of a two-diagonal square lattice of spicules have not received much attention.
Scientists recall that open-celled lattices such as those found in the skeletal system of E. aspergillumare commonly used in an engineering context due to their lighter weight, high energy absorption and ability to control acoustic and heat wave propagation. As a rule, the properties and functionality of such geometric shapes depend on the type and characteristics of the connection of their nodes (intersection points).
For example, a minimum number of nodes of six is required for two-dimensional lattices in which tension is predominant, thereby achieving a higher strength-to-weight ratio for structural applications. But lattices with simple square geometry (with a knot connection of four) are rather unstable when the load vector has a transverse component, so a diagonal connection is required for stabilization.
In the work we are considering today, scientists used the skeleton of E. aspergillum as the basis for creating mechanically robust square-lattice architectures. During the study, experimental and numerical analysis methods were used to determine the mechanical properties of the skeletal lattice of the sponge.
Research results
To better understand the mechanical advantages of the skeletal architecture of the sponge, the geometry characteristics were compared with those of the other three 2D square-base lattices (all four had the same volume, i.e. the same amount of material).
In each of these structures, the basic square architecture consisted of elements with a length L and a rectangular cross-section with a depth H that is large enough to avoid out-of-plane deformation.
Option A, which was inspired by a sea sponge, consisted of horizontal and vertical (off-diagonal) elements of thickness T A, nd = 0.1 L and two sets of parallel double diagonals of thickness T A, d= 0.05 L located at a distance S = L / (√2 + 2) from nodes ( 2 ).

Image # 2
Option B was also based on the sponge architecture with T B, nd = 0.1 L, but contained only one diagonal of thickness T B, d = 0.1 L, crossing each of the closed cells ( 2b ).
Option C (T C, nd = 0.1 L) was based on the architecture used in modern engineering applications, had a set of crossed diagonal beams with thickness T C, d = 0.05 L in each cell ( 2c ).
Option D had no diagonal reinforcement, and its horizontal and vertical members were T D, nd = 0.1L (1 + 1 / √2) (2d ).
First of all, the mechanical response under uniaxial compression along the vertical elements of the four lattice variants described above was analyzed.
Samples containing 6x6 mosaics of square cells with L = 1.5 cm and H = 4 cm were made on a Connex500 3D printer (Stratasys). Uniaxial compression was performed using an Instron device (model 5969) with a 50 kN load cell ( 2e ).
On the graph 2fshows the stress-strain curves from which two main conclusions can be drawn. First, all diagonal reinforcement designs (options A, B, and C) had nearly identical initial elastic response, demonstrating that different diagonal reinforcement designs did not affect the initial overall stiffness of the structure. Option D, as expected, showed a higher initial stiffness due to the thicker vertical and horizontal members.
Secondly, all the curves show a clear maximum load-bearing capacity, with the A structure (sponge-inspired variant) taking the highest load.
Since each maximum load corresponded to the onset of buckling, the scientists concluded that design A had the highest critical buckling stress of all the buckling options considered.
In addition, it was found that in all three structures with diagonals, the dynamics after the loss of stability led to a homogeneous transformation of the structure throughout the sample ( 2e ).
But in variant D, the critical mode led to a much longer wavelength than the size of the square cell, which, after loss of stability, led to the formation of a shape qualitatively similar to that of a compressed curved beam.
To understand how the sponge-inspired lattice design resulted in significant mechanical improvements, a finite element simulation was performed using ABAQUS / Standard software.
For modeling, the geometry was constructed using Timoshenko beam elements (element type ABAQUS B22), and the material reaction was recorded using an incompressible material model with a shear modulus μ = 14.5 MPa.
The modeling process consisted of three stages:
- buckling analysis;
- then a disturbance was applied to the grid nodes in the form of the lowest buckling mode;
- static nonlinear analysis for evaluating nonlinear responses at large deformations.
Graph 2f shows a very close agreement between the numerical and experimental results.
Further, the finite element model was intentionally extended to study the influence of the direction of the load. In order to reduce computational costs and eliminate edge effects, the periodicity of structures was used and the response of representative volume elements (RVE) with suitable periodic boundary conditions was investigated.

Image No. 3
At 3ashows the change in effective structural rigidity (E) depending on the load angle (θ). It was found that the stiffness of all structures containing diagonal reinforcement was practically the same for any load angle. This fact further confirms that the stiffness of the structure was mainly determined by the amount of material distributed along the direction of the load.
As a result, structure D, in which all material was classified as off-diagonal elements, exhibited the highest stiffness at θ = 0 °, but had negligible bearing capacity at θ = 45 °.
Further, the influence of θ on the buckling characteristics of structures A - D was studied. Effective critical bending stress (̅σ cr) of design A was higher than that of other diagonal reinforcement designs (designs B and C) for all values of θ ( 3b ). Construction D outperforms construction A in the interval 27 ° <θ <63 °, assuming that these constructions are infinite. However, given the global buckling behavior of structure D, such characteristics were largely influenced by boundary effects and the critical buckling stress was significantly reduced when considering a structure with a well-sized 10x10 RVE ( 3d ). In addition, the geometry of structure A retained its robustness even after modifications to the lattice by introducing different levels of disorder, which is consistent with the features observed in the skeleton of the sea sponge.
The above simulation and actual test results clearly show that Design Option A, based on the sponge skeleton, clearly outperforms its competitors (Options B, C and D). However, the tests were not completed on this, because the scientists wondered if it was possible to create a structure that would be even better.
To this end, an optimization problem was formulated aimed at determining the number (N) of diagonal elements of a square lattice, which would allow achieving a higher critical bending stress. It was also necessary to establish the distance between these elements and the nodes of the lattice joints S i (where i = 1, 2, ..., N), as well as the ratio of diagonal and off-diagonal elements λ = V nd / V d (Vnd and V d are the volumes of off-diagonal and diagonal elements, respectively). All these variables in one way or another affect the bending stress indicators.
During the tests, 3x3 RVE structures were subjected to uniaxial compression parallel to the off-diagonal elements (θ = 0 °). The objective function Z = ̅σ cr was maximized using finite element modeling coupled with a Python implementation of the covariance matrix adaptation evolution algorithm (CMA-ES). For each input dataset defined by the CMA-ES, finite element buckling analysis was performed to obtain ̅σ cr , which was subsequently used to estimate the objective function Z.
Seven different optimizations were performed, each of which considered a fixed integer number of diagonal elements N in the range from one to seven (N = ℤ ϵ [1, 7]). To ensure the symmetry of the system, the following rules were taken into account: S 2i − 1 = S 2i (i = 1, 2, ..., N / 2), if N is an even number; S 1 = 0 and S 2i − 1 = S 2i (i = 2, 3, ..., (N - 1) / 2) if N is odd.
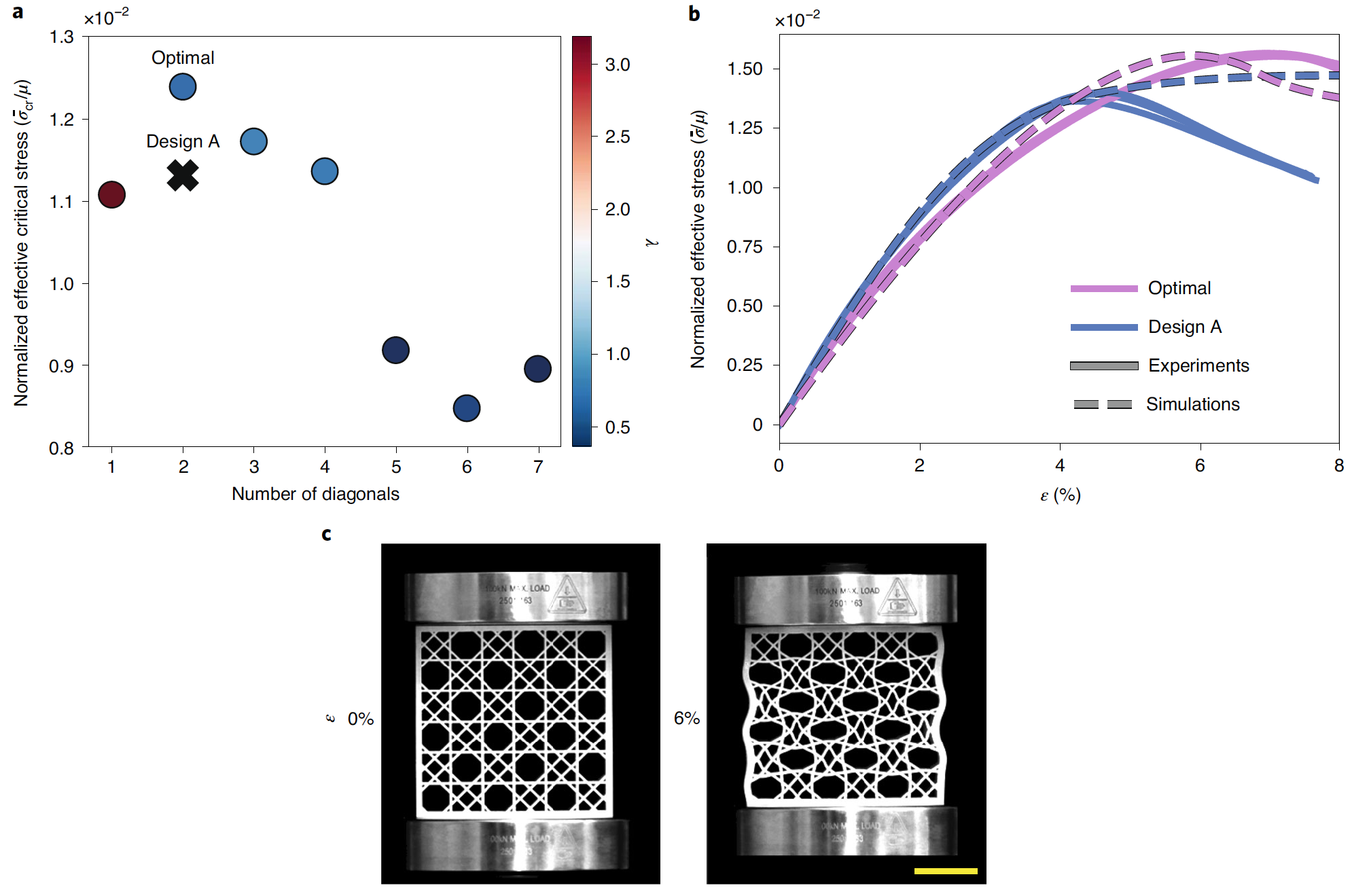
Image №4
Graph 4a shows the highest value ̅σ cr , certain model CMA-ES for all values considered N. It was found that the highest value ̅σ crwas only 9.55% higher than in the case of the previously tested design A. In this test, the modeled design was also inspired by a sea sponge: two diagonals were located at a distance of S = 0.1800 L from the nodes, and the volume distribution was such that λ = 0.6778). The simulation results have been successfully confirmed experimentally ( 4b ).
Scientists note that the skeletal structure of the sea sponge E. aspergillum is a great inspiration for more than just lattice architectures (construction A). To demonstrate this, image 5a shows a thin 11x2 square mesh mosaic subjected to three-point bending stress.

Image # 5
As experiments ( 5b) and finite element simulations demonstrated that the sponge-inspired design was stiffer and could withstand 15% higher loads over a wider range of applied displacements.
For a more detailed acquaintance with the nuances of the study, I recommend that you look into the report of scientists and additional materials to it.
Epilogue
Nature has always been, is and will be one of the main sources of inspiration for scientific research. In this work, this statement was confirmed by the example of sea sponges of the species Euplectella aspergillum, whose skeletal structure has amazing characteristics. The main feature is that this biological structure is able to withstand significant loads, while a minimum amount of material is involved in its construction. In other words, sea sponges are quite porous (roughly speaking), but very durable.
The study has shown that the architecture of the skeleton of a sea sponge can be extremely useful in a variety of areas of human activity. The introduction of the sponge architecture in construction will allow the creation of taller skyscrapers and longer bridges, while the optimal amount of material will be spent, and the strength of the finished structures will not be affected. This technique can also be used in aircraft construction, shipbuilding and even in astronautics, because minimizing the ship's mass will minimize fuel consumption.
Friday off-top:
Euplectella aspergillum ( , EV Nautilus 2014 ).
Euplectella aspergillum ( , EV Nautilus 2014 ).
Thanks for your attention, stay curious and have a great weekend, guys! :)
A bit of advertising
Thank you for staying with us. Do you like our articles? Want to see more interesting content? Support us by placing an order or recommending to friends, cloud VPS for developers from $ 4.99 , a unique analogue of entry-level servers that we have invented for you: The Whole Truth About VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps from $ 19 or how to divide the server correctly? (options available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).
Is Dell R730xd 2x cheaper in Equinix Tier IV data center in Amsterdam? Only we have 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands!Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - From $ 99! Read about How to build the infrastructure of bldg. class with the use of Dell R730xd E5-2650 v4 servers at a cost of 9000 euros for a penny?
