“I recently started experimenting with gnuplot and quickly made an interesting discovery. I plotted all primes below 1 million in polar coordinates, so for each prime p (r, θ) = (p, p). I didn't expect anything special, I just tried it. The results are impressive. "
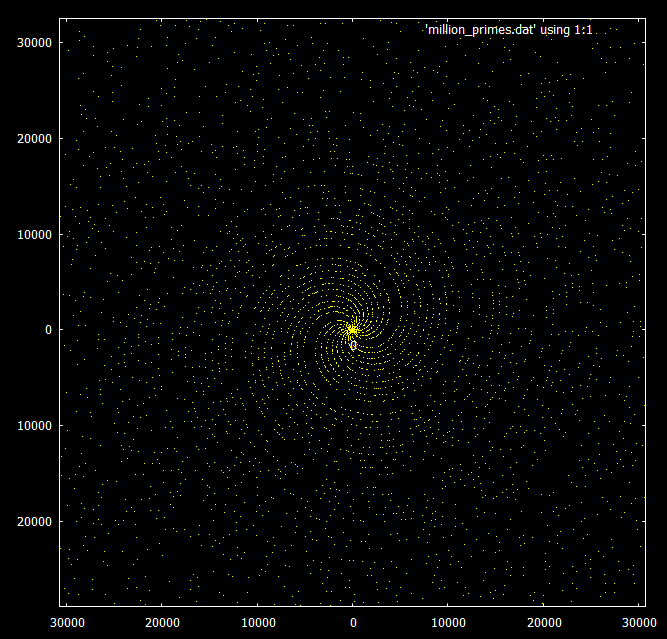
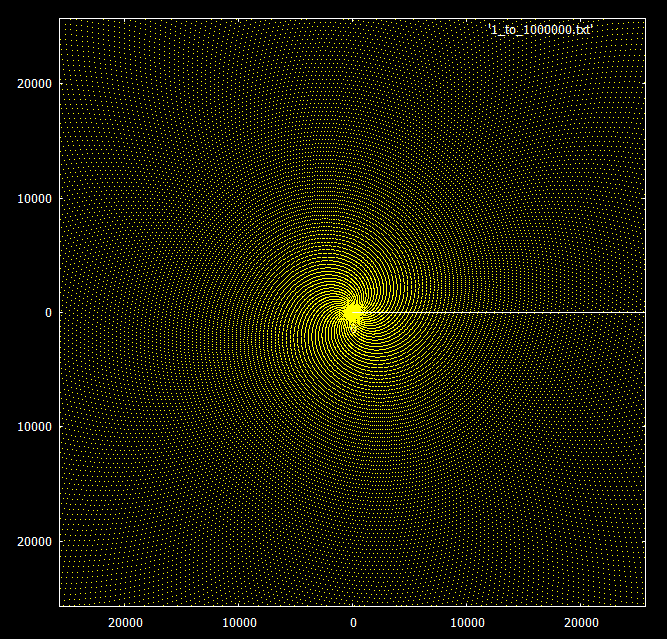
If you look at the primes below 30,000, you can see a spiral pattern.
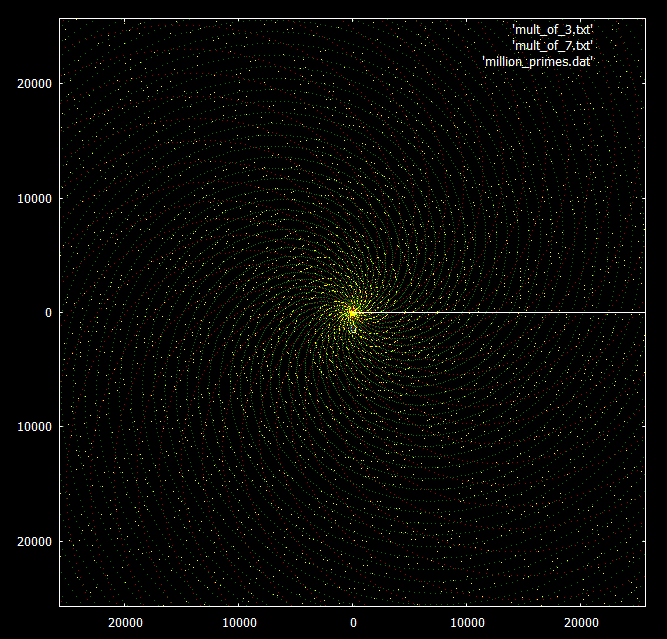
For comparison - the same graph with superimposed numbers in multiples of 3 and 7. Prime numbers are highlighted in yellow, multiples of 3 and 7 in green and red, respectively.

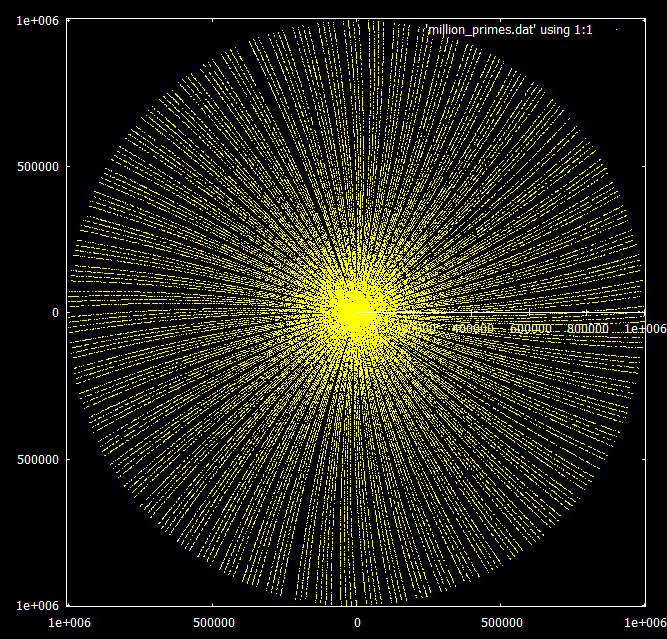
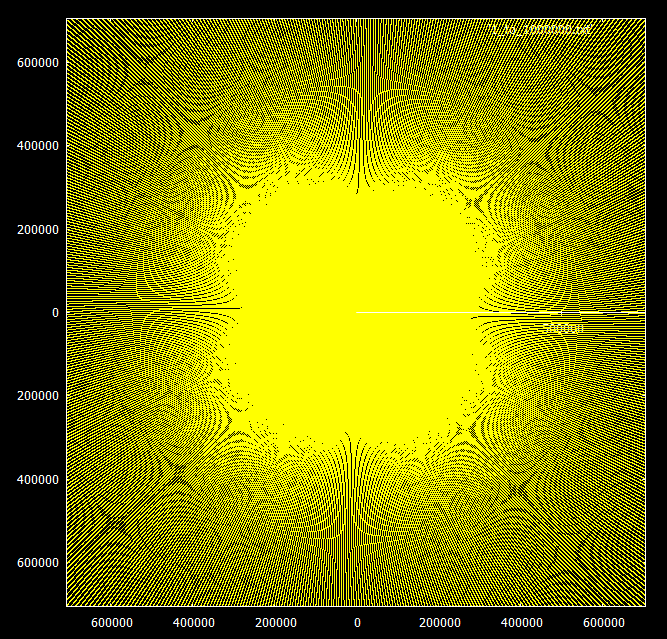
What's really interesting is the behavior when increasing the range. Multiples of this number appear to spiral in the same pattern to infinity, but the prime numbers begin to form rays in groups of 3 or 4.
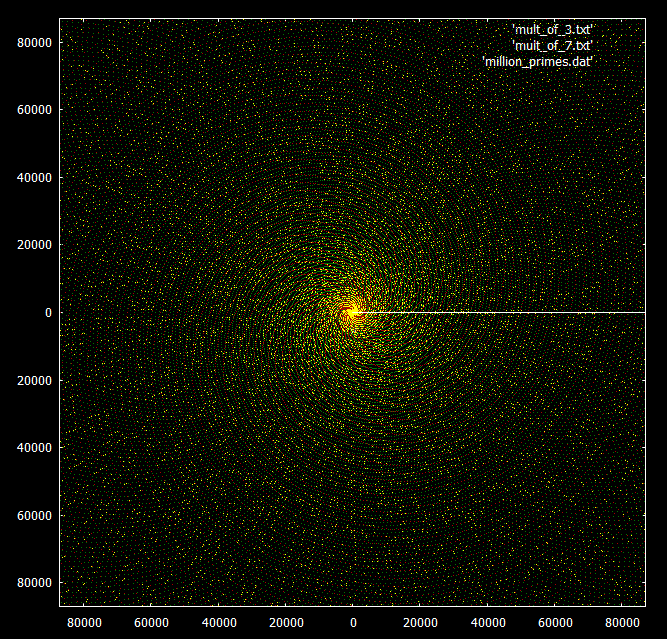
Compared to multiples of 3 and 7:
? , ?
. , , .
(, θ) = (n, n), n∈N
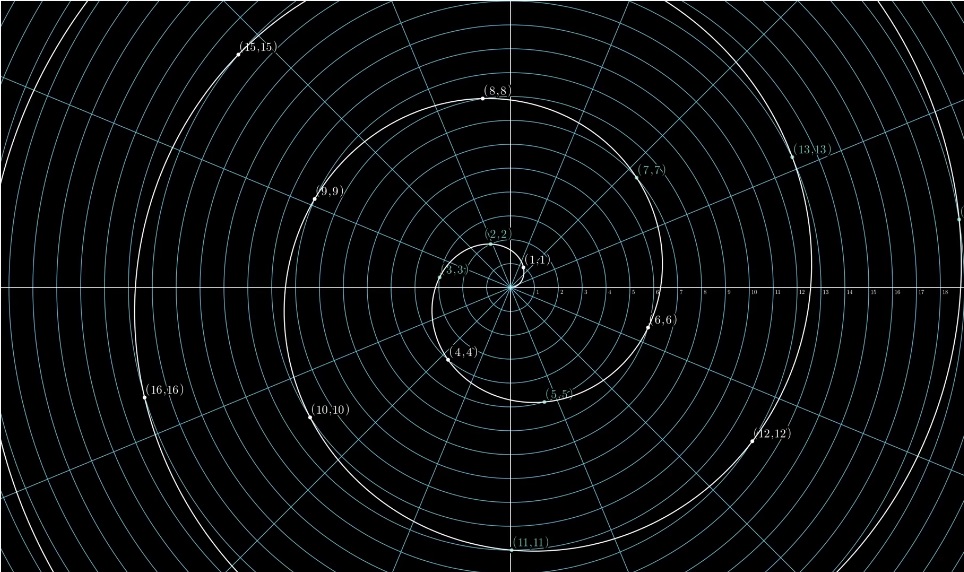
To begin with, you can play with polar coordinates and consider all points with integer coordinates: (1,1) (2,2) ...
We
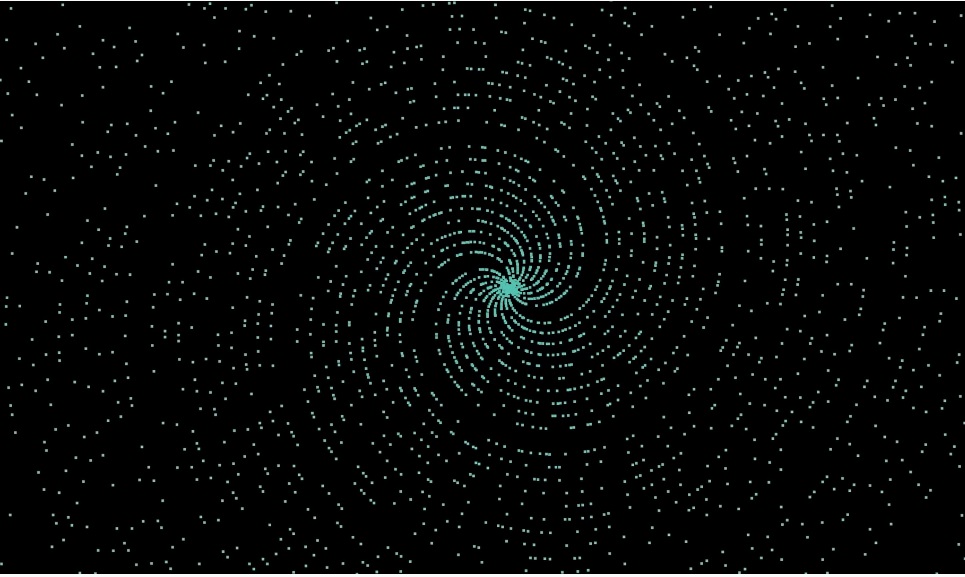
get the Archimedean Spiral: If we exclude all numbers except prime numbers, we get a spiral galaxy with spaces:
"Moving away" we can see rays directed in all directions, mostly in groups of 4:

Spirals can be counted, there are 20 of them:

A rays 280:

If we take all numbers, not just simple ones, then the spirals are even more even and there are 44:

On closer examination we have 6 spirals:

All numbers that are multiples of 6 form one branch:
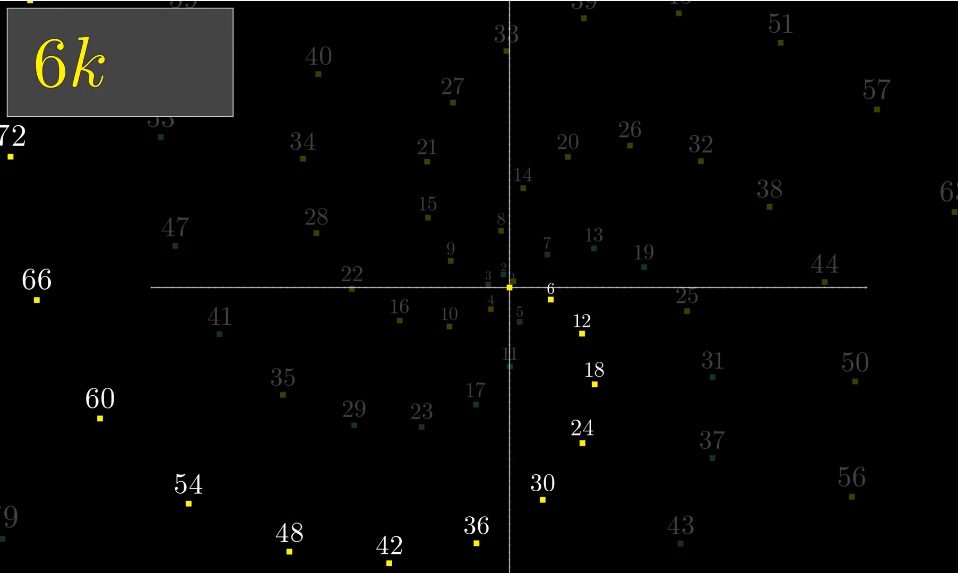
The rest of the spiral arms are 6k + 1, 6k + 2, etc. Why is that? Because 6 is roughly equal to (full revolution) 2ℼ (6.28318530718). This small difference creates the illusion of a single curve.
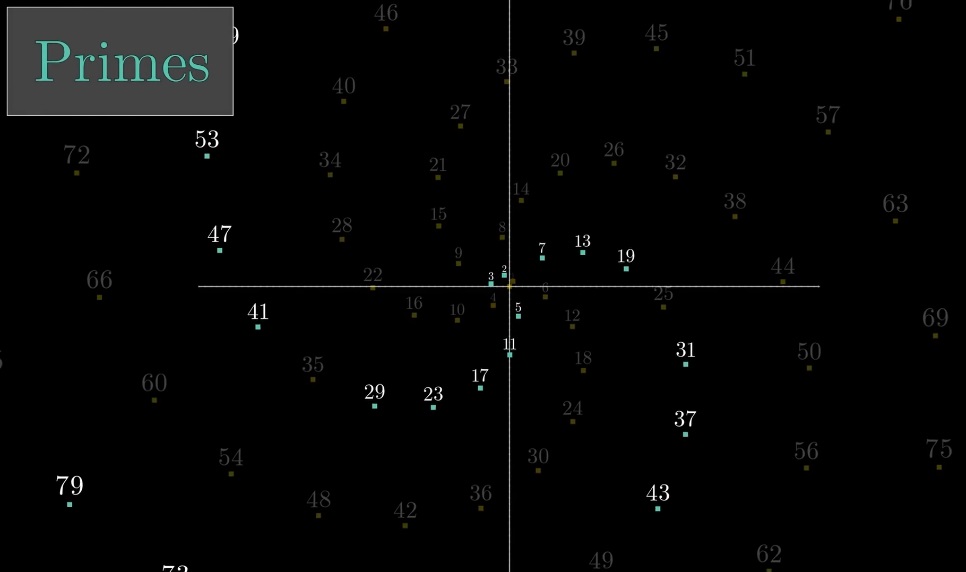
If you leave only the primes, there will be only two spirals (6k + 1 and 6k + 5):
6 - almost a full circle, 44 - an even more accurate approximation (44 / 2ℼ ≈ 7 full circles)
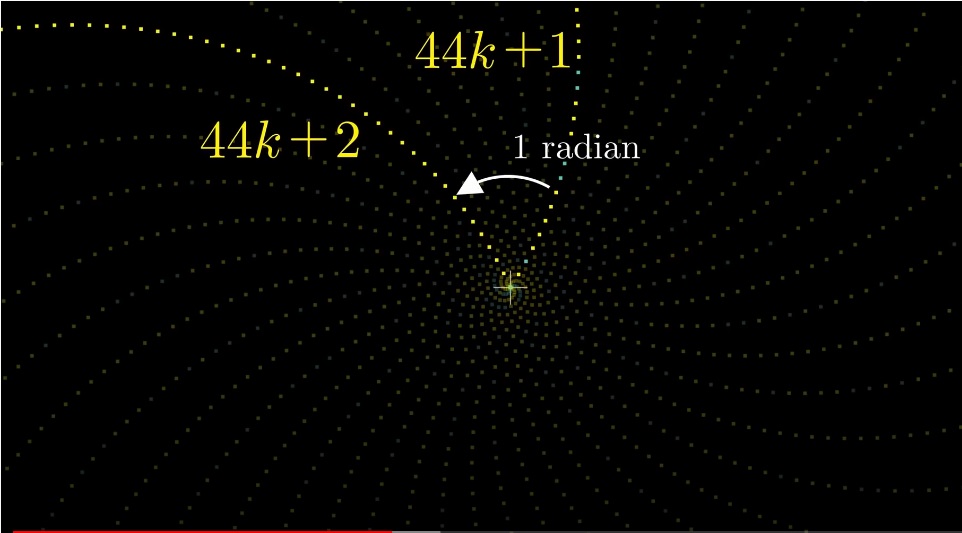
Only for primes there are 20 sleeves (44k +1, 44k + 3, 44k + 5 ...). Euler's function φ (44) = 20.

710 / 2ℼ ≈ 113. (113.00000959)

For prime numbers there will be gaps:

The further we move away, the more clearly the curvature of the entire structure becomes apparent.
710 = 71 * 5 * 2. This explains the grouping of 4 beams (5) and the "broken teeth of the comb" (71):

Euler's function φ (710) = 280.
According to Dirichlet's theorem, the primes are evenly distributed over the sleeves.
Conclusion
Playing with visualization, you can stumble upon a) Dirichlet's principle b) approximating the number ℼ (and continued fractions) c) reaching the Euler function.
The spiral shape is an artifact associated with an even number of radians matching.
Movie with Russian voice acting:
PS
More work on prime numbers:
- Bounded gaps between primes . (By Yitang Zhang, 2014)
- Primes in tuples I (By DANIEL A. GOLDSTON, JÁNOS PINTZ, and CEM Y. YILDIRIM, 2009)
Continued fractions from Savvateev:
Alexey Savvateev "All about writing numbers":