
In 2017, two scientists, Canadian John Aycock and British Tara Copplestone, published an analysis of the classic game Entombed for the Atari 2600 video game console . The mechanics of this game, released in 1982, are extremely simple: the archaeologist, controlled by the player, must make his way through the scrolling catacombs from the bottom up, dodging zombies.
The Atari 2600 only had 128 bytes of RAM; nevertheless, the seemingly endless maze was new with each launch; generated in memory. How did the programmers manage it? Here is a comment by Stephen Sidley, the programmer who created this game 38 years ago:
- . , , . , , , , , .
Wikipedia lists a dozen different algorithms for generating mazes. Of greatest interest for game consoles is the " Eller algorithm ", created in the same 1982 by Martin Eller from Microsoft. Eller's algorithm allows you to create connected mazes line by line without loops, and to generate a maze of unlimited height, it is enough to store only the last couple of lines in memory. It would seem that this is exactly what Entombed needs! But alas, Eller's algorithm is incompatible with the game mechanics of a vertical scroller, because in the resulting maze you regularly have to go around obstacles from above. To demonstrate this, I slightly modified Eller's algorithm so that the maze is created in a matrix of "walls" and "passages", as in Entombed:
More sophisticated algorithms using recursion and the like would not fit in 128 bytes of RAM. So, the requirements for the algorithm for Entombed are:

- Line-by-line generation of mazes of unlimited height;
- The created mazes should have as few disconnected sections as possible; (the player has a limited ability to "break through walls", so rare incoherence is not a problem)
- Created mazes should consist mainly of branching and connecting vertical passages - so that the passage of the maze does not require upward movement;
- Only the last few generated lines should be used to generate new lines of the maze. (Since the Atari 2600 does not have a video buffer, all the lines of the maze visible on the screen must be stored in some form in 128 bytes of main memory).
Who and how created this algorithm?
Two scientists who call themselves "video game archaeologists" decided to start their research with Entombed - a game about an archaeologist in a maze. During their research, they tracked down Stephen Sidley and asked him what algorithm he used to generate the maze. As already mentioned, Sidley told them that even the author of the algorithm could not remember what his algorithm was, and Sidley himself, even more so. Then the researchers tried to find the "junkie" who created this algorithm; the second half of the story was found in an interview published in 2008:
Entombed [Duncan Muirhead] [Paul Allen Newell]. - , , , . , . , VCS [Atari 2600], . , . , , . , Towering Inferno, using part of our algorithm there, and quit. After I left, the firm hired Stephen Sidley and handed over the maze generator to him. He had to delete a significant part of my code to make room for game mechanics. [At the Atari 2600, in addition to the severe restrictions on the amount of RAM and ROM, it is also a requirement that the generation of each row of pixels takes exactly 76 cycles author's note ].
Sidley mentioned that the maze generator code was written in 6502 assembly without any comments. This in itself looks like a feat: as noted khim, there "the set of commands is so limited and crooked that when writing programs, the main question arises," how can I write anything on this miracle? " Nevertheless, the researchers dug into the game code and found out that the maze is generated as follows: for each of the eight cells of the generated row, five already generated cells are considered (three on top and two on the left), and in accordance with the "magic table" the state of the new cell is selected (passage, wall, or random choice). The two leftmost cells are always full and are not stored in memory. The right half of the maze is just a mirror image of the left.

A mysterious table at the heart of an unsolved algorithm
 The properties of the generated maze depend on the state of the new cell set for each five previously generated. Table sewn into Entombed, many puzzled researchers: "We did not notice it any laws, even when we have several ways to present it in the form of a Karnaugh map ." Sidley said in the same vein: "For me it remains a mystery: I could not unravel it, and used it as a black box." However, the absence of regularities in the table is a bit of an exaggeration: for example, on the Karnot map, you can see that when c = 1 (the wall to the top left of the current cell), X = 1 (the wall in the current cell) will not be generated .
The properties of the generated maze depend on the state of the new cell set for each five previously generated. Table sewn into Entombed, many puzzled researchers: "We did not notice it any laws, even when we have several ways to present it in the form of a Karnaugh map ." Sidley said in the same vein: "For me it remains a mystery: I could not unravel it, and used it as a black box." However, the absence of regularities in the table is a bit of an exaggeration: for example, on the Karnot map, you can see that when c = 1 (the wall to the top left of the current cell), X = 1 (the wall in the current cell) will not be generated .
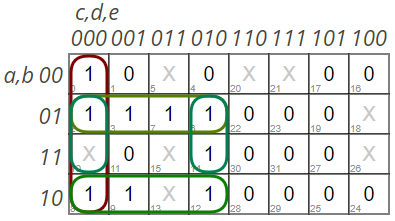
BBC in its reportabout “digital archeology” she resorted to even more dramatic exaggerations: “The table is truly ingenious: every time you start the game, a new maze is created, through which you can go from beginning to end. If the values in this table were even slightly different, then most likely the maze would turn out to be impassable. It's just inexplicable. " The repost on hackaday.com is formulated even more confidently: "A mysterious table always creates passable mazes, but if you change any bits in it, and the puzzle will become insoluble." In fact, the labyrinth was not always coherent, as can be seen in the video of the game ; and small changes in the table do not have a noticeable effect on the resulting mazes: I made a JavaScript version, in which you can play with the "mysterious table" yourself - change it right "on the go" and watch how the labyrinth changes as a result. Probably, the guarantee of maze connectivity, which Paul Newell mentioned in his interview, was lost along with the deleted part of the code.
Archeology of video games
John Aycock commented on how Entombed became the subject of his research: he was preparing a reverse engineering task for his students, and he chose a relatively little-known game, because for popular games students could find already parsed code on the net. If such an outstanding find was found in a game chosen at random, does it mean that in almost any game of that time there will be brilliant programming solutions, you just have to dig a little deeper? Stephen Sidley compared designing for the Atari 2600, with its meager instruction set, 128 bytes of RAM, and 76 clocks per line of pixels, to "climbing Mount Everest without oxygen tanks" : the very limitations of the platform forced programmers to invent ingenious algorithms.
Digging deeper is not just a metaphor. Research into classic video games is complicated by both the fragility of the media they were recorded on and the treatment of old games as uninteresting rubbish. In 1983, Atari dumped 47 tons of Atari 2600 cartridges in a landfill - no less than a dozen full trucks! Crushed by an asphalt roller and poured over with concrete, these cartridges lay for thirty years until, in 2014, "digital archaeologists" received permission to excavate and retrieve the surviving cartridges. None of the dug cartridges worked, but at least one of them was restored by soldering the components.
The behavior of Atari, who poured concrete in cartridges to protect them from "thieves", is very typical of copyright holders who would more easily consign their work to eternal oblivion than suffer "lost profits" from the fact that their intellectual property will be given to someone for free. But perhaps it is not too late to protect the "virtual cultural layer" of the 20th century by allowing free copying of programs that have long lost their commercial value?
