
Other cycle articles
In this IV part, we complete the description of the AES-128 cipher. For readers who are not familiar with the previous parts of the work, I will explain that the material is presented for educational purposes and this imposes a number of features (detailing, numerical examples, mathematical foundations, etc.) It is not just intended to familiarize yourself with the standard , and the use of the material presented for the development of encryption and decryption algorithms (in the absence of a key). The authors of many well-known online (and offline) publications did not set themselves such goals, which makes these publications of little use for our purposes.
The reverse process of encryption is called message decryption. To decrypt (with a key) ciphertexts (ST), an inverse substitution table and round keys are created, which are used in reverse order relative to the encryption scheme, but similar to the encryption process.
Decrypting AES Messages
The list of operations for decrypting a message remains the same as for encryption. More details on operations can be found here . This is a fairly general principle of ciphers - a single hardware implementation for encryption and decryption, which is provided by sets of the same functions for both processes. Only the source text and the sequence of key submission are changed.
The process of decrypting messages is implemented as a sequence of reverse (inverse) transformations used for encryption, in the reverse order of their sequence during encryption. It is also obvious that the round keys are used in the appropriate sequence: first, the key received last, then the penultimate key, and so on until the first round key.
All transform names remain the same, but are prefixed with Inv. We will consider them in the same sequence as before. The AES cipher allows two decryption options, reverse and forward, which are discussed in detail below.
Reverse decryption option
Reverse decryption of a message is a natural process of reversing the encryption process.
The AddRoundKey operation remains the same (unchanged) S + Ki for all 16 bytes of the State as it was when encrypting the message, i.e. is the inverse of itself. This is due to the fact that XOR logic is used in the operation, and bytes are representable in binary numbers.
The key of the last round is simply added (summed up) to the encrypted message.
InvSubBytes. The essence of this transformation has not changed, that is, each byte of the message being converted is replaced with another one taken from the table (S -1-block) replacement. Of course, the substitution table is different here. The byte {x, y} is replaced by the byte from Inv S (x, y) according to the same principle: x - table row, y - its column. The replacement byte is retrieved from the cell at the intersection of row (x) and column (y) of the Inv S (x, y) table.
As before, the size of the table is 16 × 16 = 256 bytes, each of which is obtained by vector-matrix multiplication and subtraction (affine transformation) from the product of the shift vector C. In binary fields, the addition and subtraction operations are equivalent, so the vector C can be simply added to product. The InvSubBytes table is shown below. The specified node of substitutions S -1 is presented in the following table 1, the values are given in hexadecimal format:
Table 1. Table of substitutions of the inverse S -1 - block

The table shows examples of replacements of two bytes 4A → 5C and 9F → 6E filled with green.
InvShiftRows. This transformation shifts the rows in the table (the State square) to the right (in the direction opposite to the original shift). The shift value for each row remains the same: the first (top) row is not shifted c0 = 0, the second is shifted by c1 = 1, the next one is shifted by c2 = 2, and the last one is c3 = 3 positions (cells). The values c0, c1, c2, c3 were given in the table and in the figure earlier for the first round of message conversion.

The result of such multiplication in the scalar representation is:
S'0C = ({0l} · S0C) {({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C);
S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);
S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);
S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).
To obtain IT from PCs, the decryption algorithm uses the same parameter values that were used in the encryption process. For the formation of the expanded key, the rules remain the same.
Direct decryption option
Peculiarities of the decryption algorithm for some inverse transformations make it possible to preserve the same sequence of operations as in the encryption algorithm, but some of the parameter values require changes. First of all, we are talking about the key (its unfolding).
Research has shown that the order of the SubBytes () and ShiftRows () functions does not change the value of the result, that is, these functions are permutable (they commute). This position (property) is also true for the functions InvSubBytes (), InvShiftRows (). This pattern is easy to explain. The point is that both functions operate on integer bytes, and the shifts are performed by an integer multiple of a byte, and do not change the value of the bytes themselves.
Note the following about the MixColumns () operation. It is linear to the input bytes (data).
InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR
InvMixColumns (Round Key).
These features of functions (properties) allow changing the order of their application, i.e.
InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).
AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),
but provided that the columns (32-bit words) of the expanded decryption key were previously passed through the
InvMixColumns () function .
The foregoing means that the way of decryption of the PC can be made effective by preserving the order of using the functions adopted for encryption. Obviously, in this case, the costs of hardware and software implementation of the cipher are significantly reduced. The changes concern only the procedure for generating the key deployment.
In the InvMixColumns () function, you need to convert the type of the variable, the input parameter of the function is a two-dimensional byte array (square), and the expanded key is formed as a linear (string) array of 32-bit words. For this reason, it is necessary to perform type matching to the square.
Let us show, using the example of a 2-round transformation, two equivalent versions of the RIJNDAEL decryption procedure. The first option is the usual inverse of the encryption function. The second option is obtained from the first by changing the order of operations in three pairs of transformations
InvShi ftRows () → InvSubBytes () 2 times and
AddRoundKey () → InvMixColumns () 1 times.
The result of the transformation is saved when passing from the original to the reverse
sequence of operations in the specified pairs.
From the table we see that the encryption procedure and the second variant of the decryption procedure coincide up to the order of using round keys (when performing AddRoundKey operations), replacement tables (when performing SubBytes () and InvSubBytes () operations) and transformation matrices (when performing MixColumns ( ) and InvMixColumns ()).
Table 2 - Sequence of transformations in the two-round version of RIJNDAEL

A similar result turns out to be true for any number of rounds.
Recovering a cipher key using the last subkey
Generation of round AES cipher keys. The Key Schedule for generating round keys from a 128-bit original cipher key is a recursive function. This function is discussed in detail here . The initial conditions for its launch are the first 4 4-byte key words (4 × 32-bit words), ie W [0], W [1], W [2], W [3].
Let us formulate the problem of recovering this 128-bit cipher key as follows: Let the components of the round 10 round key W [43], W [42], W [41], W [40] be found.
It is required to recover the full cipher key with only this round key.
It is convenient to consider the solution to the problem first on numerical data. Let's take the numerical example given in FIPS PUB 197 as a basis.... Table 3 contains the round 10 key.
The procedure for generating round keys is organized in such a way that it provides forward movement (unfolding of the key) along a number of previous key values. To move backward from some point of a series of values, it is necessary to have the initial data of the computation process at this point of return. Let the point of return will be the last step of the last 10 rounds, that is known for the four 4-byte 10 round key word Nk = Nb = 4...
Table 3 - 128-bit key AES encryption round 10

Next results and recovery actions for the key algorithm placed convenience into table 4, which is similar to a (kind of overturned) key generation table.
Table 4 - Recovery of the cipher key from the known key of the 10th round

Explanations for Table 4. The round numbers are counted in reverse order from the 10th to the 1st. Three columns (3, 8, 9) of the table contain ready-made keys with different current numbers depending on the i line number. The remaining cells contain auxiliary data for intermediate calculations. Thus, the value of the key W [i] appears in the table three times in three columns.
Columns 1 and 2 are the number r of the round and the ordinal number i of the 4-byte key word. The last such word during encryption has the number i = 43. In the table we write it in the top line of the right (9) column. The numbers i of the rows of the table are decreasing and in column 9 they correspond to the words of the key W [i]. The 8th column contains the word W [i - Nk] of the key with a reduced number W [43 - 4] = W [39], and the 3rd column - the key word W [i - 1] = W [42], previous W [i] = W [43].
The meaning of the word W [39] in the 8th column is unknown and we find it from the initial data using the formula:
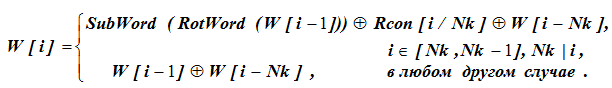
For formula calculations, the conditions for selecting the formula line are first checked. For W [43], i = 43 and Nk does not completely divide the value 43, that is, for i = 43 the value of W [i] is determined by the bottom line of the formula: W [43] = W [42] W [39]. Here, for the given values of W [42] and W [43], the last term W [39] is not defined.
Then W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.
In mod2 binary arithmetic, addition and subtraction operations are equivalent, therefore, bitwise calculations for each of the 4 bytes of the keyword W [39] take the form (Table 5):
Table 5 - Byte calculations of the keyword W [39].

Thus, the value of the keyword W [39] = 575c006e was found. We transfer this value to the 3rd column, to the i = 40 row and to the 9th column to the i = 39
row . Calculations in the i = 40 row are carried out as when expanding the key.
The unknown word W [i - Nk] = W [40 –Nk] = W [i = 36] should be determined as in the previous case by the difference W [36] = W [40] 7 column of line 40.
In turn, the value in 7- The th column of line 40 is formed as the sum (OR) of the 5th and 6th columns. The 5th column value is obtained from W [39] after a RotWord cyclic shift (4th column) and a SubWord replacement operation (5th column).
The results of these actions take the form
RotWord (575c006e) = 5c006e57; SubWord (5c006e57) = 4a639f5b.
The value in the 6th column is obtained as a constant
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9 .
This constant is represented by a hexadecimal byte
2 9 ≈100000000 = x 9 , but there is no such byte in the GF (2 8 ) field : you need to find the remainder of the division by an irreducible polynomial, i.e.
After including the constant in the keyword, we have
Rcon [j = 40 / Nk] = 36000000 (6th column). The value of the 7th column is obtained as (7th column) = (5th column) ⊕ (6th column) = 4a639f5b⊕36000000 = 7c639f5b.
And finally, for
W [36] = W [40] (7th column of row 40) = d014f9a8 7c639f5b = ac7766f3.
Further calculations by analogy lead to the final result - the cipher key.
There is more information on w and RotWord, Rcon and SubWord functions. Suppose that we denoted by Kr [j] - the j-th byte of the r-th round key and w [i] as in the documentation.
We get: Kr = (w [Nk ∙ r], w [Nk ∙ r + 1], · · ·, w [Nk ∙ r + Nk - 1]).
For different i we have the following relations
for i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr +1), w [i] = w [i - Nk] xor w [i - 1] and
for i = 0 mod Nk, w [i] = w [i - Nk] xor SubWord (RotWord (w [i – 1])) xorRcon [i / Nk].
Therefore, for i ≠ 0modNk, Nk 0≤i <Nb ∙ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] and for i = 0modNk, w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk – 1])) xorRcon [i + Nk / Nk]
With AES-256, you need to add a Subword operation when i is comparable to 4mod Nk. So it is possible to deduce the previous key from the final subkey and step by step get the value K0 of the cipher key.
The mathematical foundations of the AES - 128 cipher are quite complete and detailed here .
Let us turn to the field mapping ℓ: GF (2 8 ) → GF (2 8 ); x → x 2 + x. The image of this map
1 = Im (l) has dimension dim GF (2) (1) = 7.
Equation x2 + x = θ, where θ 1 has two different solutions (roots of the equation) 1, 2є GF (2 8 ).
According to Vieta's theorem, x1⊕x2 = 1, the sum of the roots is equal to the coefficient of the equation at x 2 with the opposite sign, and the product of the roots x1⊗x2 = θ is equal to the free term of the equation (in our equation with the opposite sign).
It is known that in the arithmetic of binary fields, the operations of addition and subtraction of elements mod2 are equivalent.

Thus, the roots of the equation are related by the ratio x2 = x1⊕1, since the coefficient at x in the equation is 1. This means that in the decimal representation of the field elements in their lexicographic ordering, they are located one after the other, differing only by one.
So for x = 0 and x = 1 and for x = 2 and x = 3 we get:

The results (images) of the mapping in the reduced pairs (0, 1); (2, 3) completely coincided, i.e. two types correspond to one image. Consequently, the cardinality of the image is two times less than the cardinality of the preimage and its dimension of its elements is 7.
The product of pairs of roots, that is, the free term of a quadratic equation is conveniently determined through the power representation of the elements of the field (inverse images). In this case, the exponents are summed up mod255, i.e. modulo the order of the multiplicative group of the field GF (2 8 ).