I have already written about my reverent attitude to Bayesian networks of trust (BSD) in the previous article . A very simple model for analyzing investor decisions on the exercise of a call option on a share is also detailed there. This time, I propose to delve deeper into the topic and build a BSD, which can already serve as the basis for a more serious decision-making support model for buying / selling shares of an oil company.
I will note in advance that I did not invent this example, and I will even indicate the source [1]. However, the source, as is often the case, missed a lot of details, which leaves a residue of dissatisfaction, and students have just a misunderstanding, which leads to the fact that they step over this material without understanding it to the end. And the task is worth it, if only because it skillfully used almost all the basic "tricks" of the BSD, and if you disassemble it "to the cog", then you can confidently move on.
As you know, traditional financial models have focused on historical and quantitative relationships between variables. However, in practice, experienced financial analysts always try to connect historical data with current market information of any kind, and understand how this information affects the returns on stocks, market sectors, interest rates, and other parameters that characterize the portfolio model. For example, at one time the antitrust investigation against Microsoft influenced the profitability of many companies' stocks, but it turned out that such information is difficult to take into account in traditional models of profitability [1]. Bayesian networks, on the other hand, easily perceive such variables in their structure.
Another disadvantage of traditional models is their static nature, often the inability to refine the results in the process of obtaining new information. Here, we also note that the way variables are represented in the BSD allows the analyst to quickly enter new information, and immediately see its impact on the entire network, and not just on the final result.
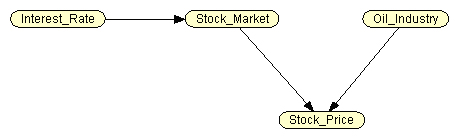
So, we are interested in the state of the oil company's stock. Let's construct an OBD of four nodes, displaying the following random variables (Fig. 1):
- Interest Rate (IR) - interest rate level (parent node);
- Stock Market (SM) - the state of the stock market;
- Oil Industry (OI) - the state of the oil industry (parent node);
- Stock Price (SP) - the level of the stock price of the researched company.
(. 2). , : «» «». , , 75% .
«» « ()». , , 40% . , (), (. . 2, ).
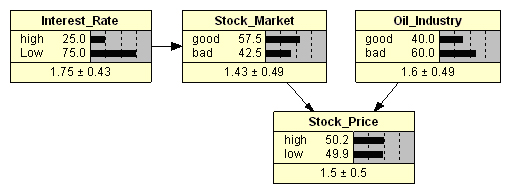
() « » - , , ( ) (). , , , , .
(. . 1). , () , ( ) . 80%. ( ), 70%. 100%, .
1. .
|
, % |
|
|
|
|
|
|
|
20 |
80 |
|
|
70 |
30 |
(. . 2) , .. , , . , 8 , «» .
, (1- ) , 80%. , (4- ) 10% . , , (2- ), « » , , 60%. , , (3- ), 50/50.
2. .
№ |
|
, % |
||
|
|
|
|
|
1 |
|
|
80 |
20 |
2 |
|
|
60 |
40 |
3 |
|
|
50 |
50 |
4 |
|
|
10 |
90 |
, Netica (. 2), . : ? , , , :
SM good = 0,25 · 0,2 + 0,75 · 0,7 = 0,575
SM bad = 0,25 · 0,8 + 0,75 · 0,3 = 0,425
! . , , . , , , , , .
– , . :
P(SM, OI, SP) = P(SP| SM, OI) · P(SM) · P(OI)
«» . , ( ) , , :
SP high = 0,8 · 0,575 · 0,4 + 0,6 · 0,575 · 0,6 +
0,5 · 0,425 · 0,4 + 0,1 · 0,425 · 0,6 = 0,5015
SP low = 0,2 · 0,575 · 0,4 + 0,4 · 0,575 · 0,6 +
0,5 · 0,425 · 0,4 + 0,9 · 0,425 · 0,6 = 0,4985
(. 2), ( ) . , , .. «» , .
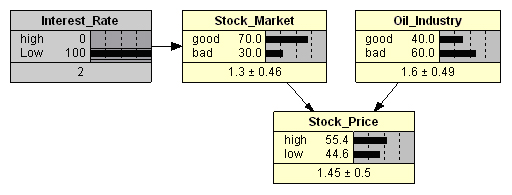
, , . , : « » «Low» (. . 3). , , 5,2% ( 55,4%). , « » « » ( ), .
, , « » (. . 4) – 71%.
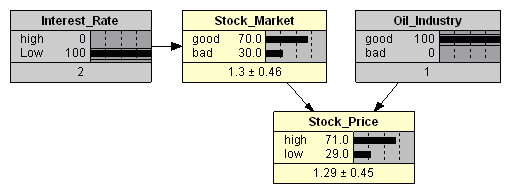
: « » « » (. . 5) 56%, .
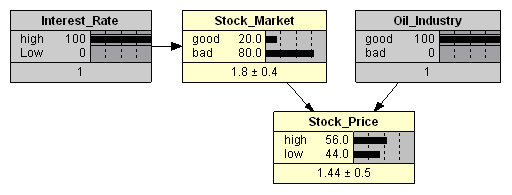
(. . 6) ( 80%) .
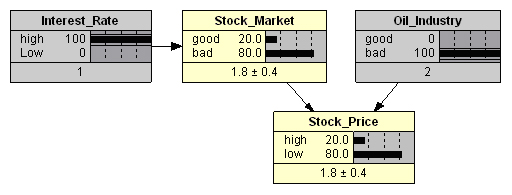
, , (. 7), 90%.
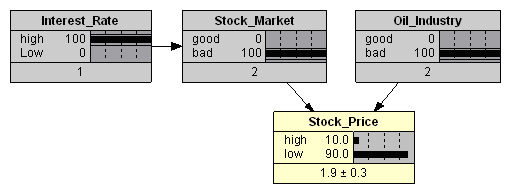
, . «» . , «» , , , , . , Netica, , , - - .
In addition to the promised source [1], I also cite a completely new book [2], in which there is a lot of useful information on the topic in Russian translation as well.
Literature:
1. Shenoy C., Shenoy P. Bayesian Network Models of Portfolio Risk and Return. Computational Finance. The MIT Press, 1999, pp. 87-106.
2. Sukar L. Probabilistic graph models. Principles and applications / per. from English Moscow: DMK Press, 2021.