Hello, Habr! When solving the problem of the maximum flow, I was faced with the fact that in all the sources I know, a formal description of the algorithms themselves was given, which made it very difficult to understand the material presented. And in this article I will try to disassemble the Ford-Fulkerson Algorithm at a basic level with a specific example, so that after reading this article, you at least understand the basic essence of the algorithm itself.
Formulation of the problem
We have the following directed graph , in which the edge weight denotes the capacity between vertices. It is necessary to find the maximum flow that can be passed from source to drain
.
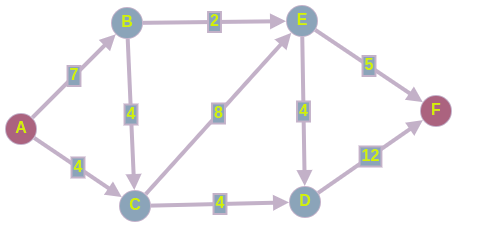
How does the algorithm itself work?
The residual network should be understood as the same graph that is at the input, but in this case we will perform some operations on it:
Send a certain amount of flow from the current vertex to the neighboring ones.
Return a certain amount of flow from neighboring vertices to the current one.
At the initial moment in time, the flow that we want to pass through our network should be equal to zero. The residual mesh is the same as the original mesh .
. , , .
, .
, .
( , 0) . , , .
.
, , .
, , .
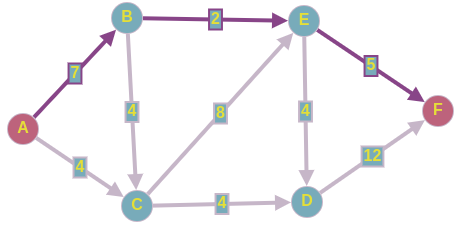
???
-2 .
, .
:
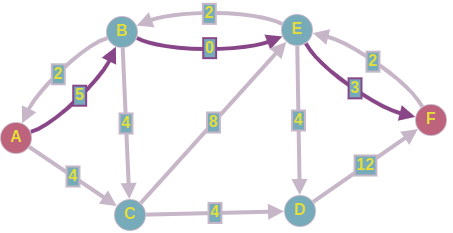
. , 2 .
, ,
.
, 2- :
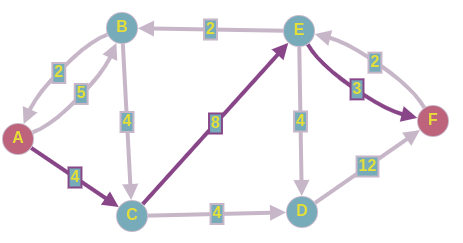
3
. , .
:

3- :

1 .
.
:

4- :
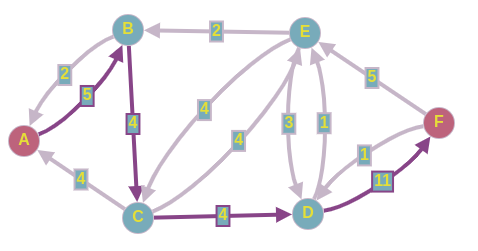
4 .
.
:
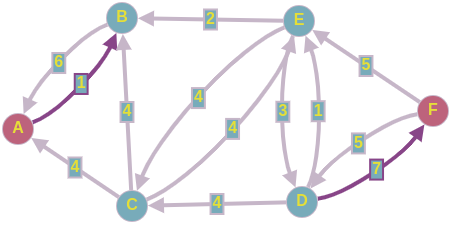
- , . .
: 10 .
, , !
!