Clever Geek Handbook

Fast Hough Transform: from Elbrus to COMDIV

For five years, we at Smart Engines have been telling you how we optimize our software for the Elbrus processor architecture. Usually we share with you enchanting results, when on Elbrus we manage to recognize almost as fast as on top foreign processors. Today's article is devoted to the description of the optimized "internals" of one algorithm that is extremely important for all computer vision systems - the fast Hough transform. In addition, we will tell you about another extremely interesting family of domestic architectures - KOMDIV microprocessors.





What is the Hough transform and when is it used?

The Hough transform was proposed in 1959 by Paul Hough as a tool for analyzing photographs of particle traces in a bubble chamber 1. By definition, the Hough transform assigns to each pattern from a certain family of lines, circles, ellipses a value equal to the sum of the values ​​of the image pixels belonging to this pattern ... Sometimes, instead of the sum, the result of other calculations of the minimum or maximum value specified on a set of operations, the calculation of the average value or the product of pixel values, etc. are calculated. By the way, in many sources such a transformation is also called the discrete Radon transform 2, 3.





- , . .





. . 4. – 2. . , , 5 6 , 7.





Visualization of applying the Hough transform to correct optical aberrations

: O (N ^ 3), N– . ? «» N. – N ^ 2, N. , – O (N ^ 3).





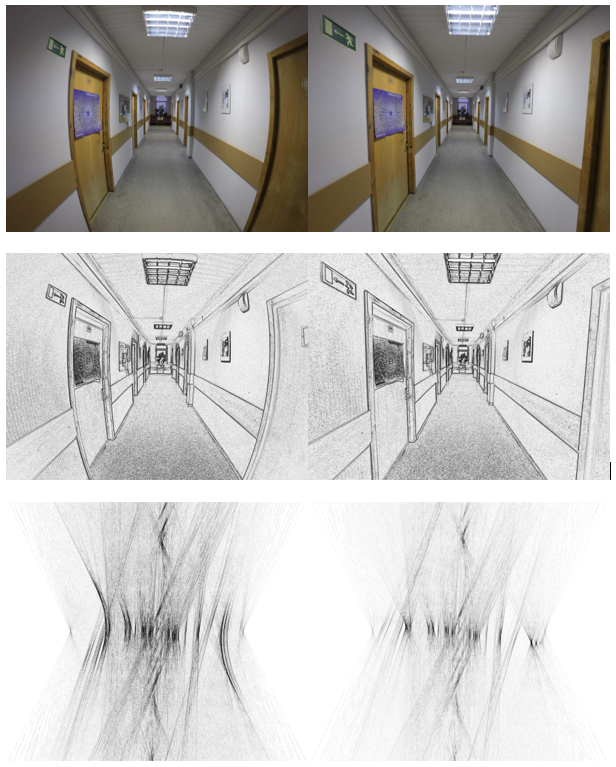
, - . 1998 .. 8. « » , , . O (N ^ 2 \ log {N}).





" ". , «» «» . , . «» «» . . N \ times N , O (\ log {N}) .





(s, 0) (s + t, N), s – , t – , N – . (s, t) -, .





Parametrizing a dyadic pattern

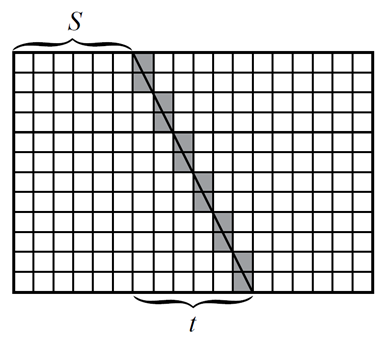
. N \ times N N = 2 ^ k, k \ in \ mathbb {N}. MATLAB, 9.





function h = fht2(I)
n = size(I, 2);
if n < 2
h = m;
return
end
h = mergeHT(fht2(I(:, 1 : n / 2, :)), fht2(I(:, (n / 2 + 1) : n, :)));
end

function h = mergeHT(h0, h1)
[m, n0, o] = size(h0);
n = 2 * n0;
h = zeros(m, n, o);
r = (n0 - 1) / (n - 1);
for i = 1 : n
t = i - 1;
t0 = round(t * r);
s = t - t1;
h(:, i, :) = h0(:, t0 + 1, :) + [h1(s + 1 : m, t0 + 1, :); h1(1 : s, t0 + 1, :)];
end
end

, . , N , N = 2 ^ k – . , , -. , , « », , , .





, , «» , MATLAB:





  • ;





  • .





«» . . , , .





«» – . , fht2core



. , mergeHT



, , . , [0; N-1] -. , , 2N-1. – , mergeHT



.





FHT

, . « », . .





, , . , EML, .





, , .





, , :





  • , Smart ID Engine «»;





  • , Smart Document Engine ;





  • , Smart Tomo Enine Pentium ;





  • , , .





. ?

. -64. ?





-64 – 64- , - . MIPS IV ISA.





18909 65 , 1 80 .





SoC 18909 CPCA. CPCA 64 , , – 4 SIMD. 64 64 64- . 16 16 . / , – 16 / . CPCA MIPS64 Release 1. , 18907. 16 /. .





CPCA – 32- ISO 60559. 10 , « », . « 2x2- 2d-» « », , 8 . , CPCA 800 32 10 ./ 4 800 25.6 .





, , . CPCA 4.2 . , 2 4 – psadd, .. 6.4 800 , 4 2 , .. 19.2 / 800 . 4 / 12.8 / 800 . , 1.5 .





, DDR3 18909 400 , CPCA 6.4 / 16 / 400 1.6 /. 533 3 a/. 1.6 /. , , .





, CPCA 12% 2% . CPCA. , , CPCA . , :





  • 4 , 1 2 ;





  • 12% ;





  • CPCA, – .





mergeHT



h0



h1



n n , , . , n0 = n1 = n / 2



, . , , , , .





/ CPCA 1.5 : . 800 , CPCA 18%.





, . CPCA. , 1.88 / 32 . , , , 470 .





5439 × 5439 1.1 / 406 , 86% . . , 512 × 512 116 (49 ./), 1024 × 1024 –191 (18 ./), 2048 × 2048 – 286 (6 ./), 4096 × 4096 – 378 (1.8 ./).





. -, , ( ). -, , , , . , .





«» .





.





« CPCA», . . , . . , . . , . . , . . , «».





  1. Hough P. Machine analysis of bubble chamber pictures // Proc. of the International Conference on High Energy Accelerators and Instrumentation, Sept. 1959. – 1959. – P. 554-556.





  2. Mukhopadhyay P., Chaudhuri B. B. A survey of Hough Transform // Pattern Recognition. – 2015. – Vol. 48. – No. 3. – P. 993-1010.





  3. Hassanein A. S. et al. A survey on Hough transform, theory, techniques and applications // arXiv preprint arXiv:1502.02160. – 2015.





  4. Duda R. O., Hart P. E. Use of the Hough transformation to detect lines and curves in pictures // Communications of the ACM. – 1972. – Vol. 15. – No. 1. – P. 11-15.





  5. . ., . ., . . // . – 2017. – . 31. – №. 4. – . 331-342.





  6. Nikolaev D. P., Nikolayev P. P. Linear color segmentation and its implementation // Computer Vision and Image Understanding. – 2004. – Vol. 94. – No. 1-3. – P. 115-139.





  7. Kunina I. A., Gladilin S. A., Nikolaev D. P. Blind compensation of radial distortion in a single image using fast Hough transform // Computer Optics. – 2016. – Vol. 40. – No. 3. – P. 395-403.





  8. Brady M. L. A fast discrete approximation algorithm for the Radon transform // SIAM Journal on Computing. – 1998. – Vol. 27. – No. 1. – P. 107-119.





  9. . ., . ., . . // . – 2017. – . 17. – №. 4. – . 294-308.







More articles:


All Articles