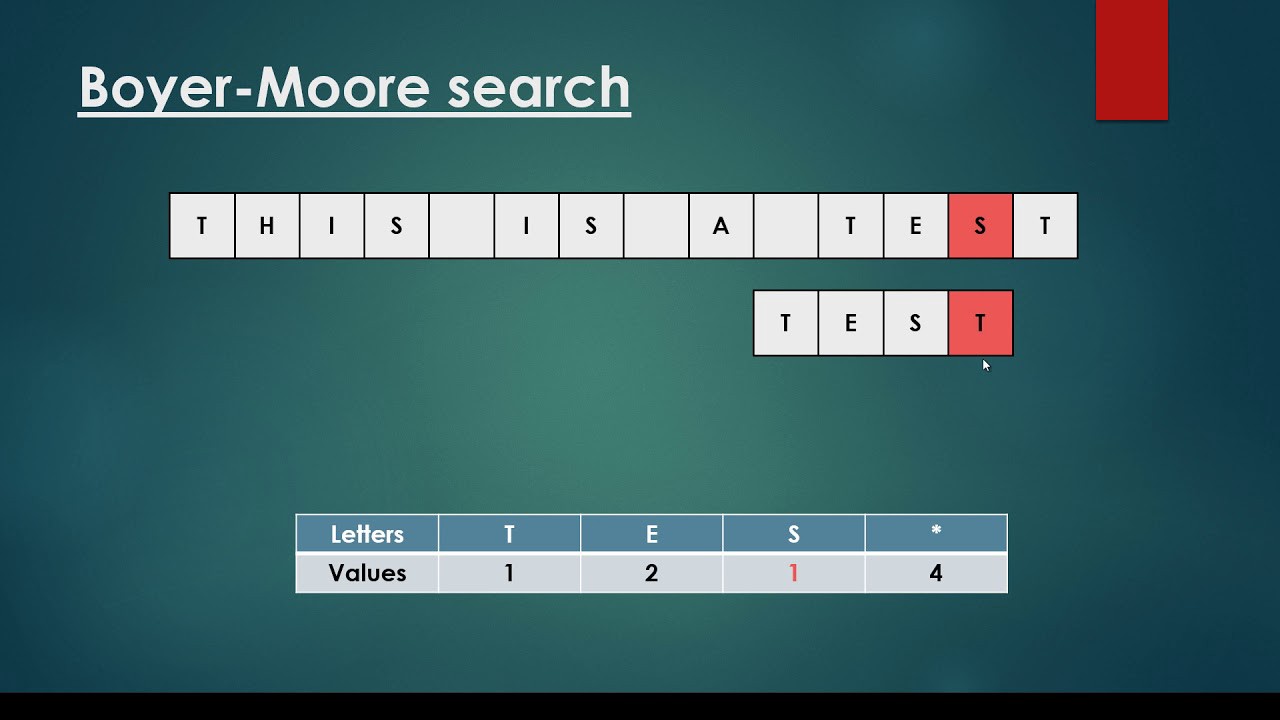
The Boyer-Moore string search algorithm is a general-purpose algorithm for finding a substring in a string.
Let's try to find the occurrence of a substring in a string.
Our source code will be:
Text: somestring
And the pattern we'll be looking for
Pattern: string
Let's put the indices in our text to see at which index which letter is located.
0 1 2 3 4 5 6 7 8 9
s o m e s t r i n g
Let's write a method that determines if the pattern is in a string. The method will return the index from where the pattern comes into the string.
int find (string text, string pattern){}
In our example, it should return 4.
0 1 2 3 4 5 6 7 8 9
text: s o m e s t r i n g
pattern: s t r i n g
If no answer is found, we will return -1
int find (string text, string pattern) {
int t = 0; .
int last = pattern.length — 1;
Let's create a loop to go through the text.
while (t < text.length — last)
? , . .
:
last = 5 ( string 5)
10 (somestring)
text.length — last = 10–5 = 5;
0 1 2 3 4 5 6 7 8 9
text: s o m e s t r i n g
pattern: s t r i n g
, 5 , 4 , ,
0 1 2 3 4 5 6 7 8 9
text: s o m e X t r i n g
^
pattern: s t r i n g
, .
:
int find (string text, string pattern) {
int t = 0;
int last = pattern.length — 1;
while (t < text.length — last){
}
}
int p = 0, .
while( p <= last && text[ t + p ] == pattern[p] ){
}
p <= last —
text[ t + p ] = pattern[p] — .
, text[ t + p ] = pattern[p]
4
0 1 2 3 4 5 6 7 8 9
text: s o m e s t r i n g
^
pattern: s t r i n g
t = 4, p = 0; text[ t + p ] = text[ 4 + 0 ] = s, pattern[0] = s, .
:
int find (string text, string pattern) {
int t = 0;
int last = pattern.length — 1;
while (t < text.length — last) {
int p = 0;
while( p <= last && text[ t + p ] = pattren[p] ){
, p .
p ++;
}
p == pattern.length
.
if (p == pattern.length){
return t;
}
.
t ++;
}
}
:
int find (string text, string pattern) {
int t = 0;
int last = pattern.length — 1;
while (t < text.length — last) {
int p = 0;
while( p <= last && text[ t + p ] == pattern[p] ) {
p ++;
}
if (p == pattern.length) {
return t;
}
t ++;
}
return — 1;
}
? ?
, .
text: some*string , ?
?
,
text: somestring
^
pattern: string
^
. , ?
, .
text: somestring
pattern: string
.
text: somestring
^
pattern: string
^
pattern[i] = ‘g’, text[i] = ’t’,
pattern.length — ’t’ .
’t’ = 1, 5–1 = 4, 4 .
text: somestring
^
pattern: >>>>string
^
.
, .
, . * .
:
s 0
t 1
r 2
i 3
n 4
g 5
* -1
, , , :
pattern:
4
2 — ,
-1
-1
5
, , .
:
int[] createOffsetTable(string pattern) {
int[] offset = new int[128]; //
//
for (int i = 0; i < prefix.length; i++){
offset[i] = -1; //
}
for (int i = 0; i < pattern.length; i++){
offset[pattern[i]] = i;
}
return offset;
}
, :
int find (string text, string pattern) {
int[] offset = createOffsetTable(pattern);
int t = 0;
int last = pattern.length — 1;
while (t < text.length — last){
int p = last; //
// ,
//
while( p >= 0 && text[ t + p ] == pattern[p] ){
p — ;
}
if (p == -1){
return t;
}
t += last — offset[ text[ t + last ] ];
}
return — 1;
}
t + last ? . , , + .
:
:
= 4
= 2
= 5
1:
0 1 2 3 4 5 6 7 8 9 10
text:
pattern:
last = 7;
t += last — offset[text[t + last]]
t += last — offset[text[0 + 7]]
t += last — offset[‘’]
t += 7–5 = 2;
t = 2;
2:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:
pattern: > >
t = 2;
t += last — offset[text[t + last]]
t += last — offset[text[2 + 7]]
t += last — offset[‘’]
t += 7–5 = 2;
t = 4;
3:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:
pattern: > > > >
t = 4;
t += last — offset[text[t + last]]
t += last — offset[text[4 + 7]]
t += last — offset[‘’]
t += 7–5 = 2;
t = 6;
4:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:
pattern: > > > > > >
t = 6;
t += last — offset[text[t + last]]
t += last — offset[text[6 + 7]]
t += last — offset[‘’]
t += 7–5 = 2;
t = 8;
5:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
text:
pattern: > > > > > > > >
.
- .
. ?
abcdadcd
. .
d, ? . 2 d 2 4. 2 .
4
-----—
| 2
| ---
| | |
abcdadcd
^
cd. d 2.
2
abcdadcd
cd,
-- 4 .
= 4.
842
abcdadcd
dcd. dcd .
--- = 8
8, .
.
* *, c , 1.
1
*
—
41
*
-—
441
*
--—
4441
*
---—
4441
*
----
For Okol we also write the 4 . Because our prefix is the same as the suffix.
Let's try to write the code for this
createSuffix(string pattern){
int[] suffix = new int[pattern.length + 1]; // +1
for(int i = 0; i < pattern.length; i ++){
suffix[i] = pattern.length; // ,
// .
}
suffix[pattern.length] = 1; // 1
// , .
for (int i = pattern.length — 1; i >= 0; i — ) {
for (int at = i; at < pattern.lenth; at ++){
string s = pattern.substring(at); //
For example, what is the bell to compare with?
--—
--—
---
---
---
, , ,
for (int j = at — 1; j >= 0; j — ) {
string p = pattern.substring(j, s.length); //
//
if (p.equals(s)) {
suffix[j] = at — i;
break;
}
}
}
}
return suffix;}
There is a more optimal algorithm, but further individually.
What code do we have at the moment?
int[] createSuffix (string pattern) {
int[] suffix = new int[pattern.length + 1];
for (int i = 0; i < pattern.length; i ++){
suffix[i] = pattern.length;
}
suffix[pattern.length] = 1;
for (int i = pattern.length — 1; i >=0; i — ){
for(int at = i; i < pattern.length; i ++){
string s = pattern.substring(at);
for (int j = at — 1; j >= 0; j — ){
string p = pattern.substring(j, s.length);
if (p == s) {
suffix[i] = at — 1;
at = pattern.length;
break;
}
}
}
}
return suffix;
}
int find(string text, string pattern) {
int[] offset = createOffset(pattern);
int[] suffix = createSuffix(pattern);
int t = 0;
int last = pattern.length — 1;
while (t < text.length — last) {
int p = last;
while (p >= 0 && text[t + p] == pattern[p]) {
p — ;
}
if (p == -1) {
return t;
}
t += Math.max (p — offset[text[t + p]], suffix[p + 1]);
}
return -1;
}
p - prefix [text [t + p]] - the last character that was found and adjust the shift of our template for it
suffix [p + 1] - The suffix value for the last element that was compared.
And we move to the maximum value in order to move as quickly as possible.
This concludes the analysis of the Boyer-Moore algorithm. Thanks for attention! =)