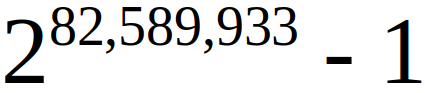
(Translator's note: I did not find publication (s) on this topic on Habré.)
Blowing Rock, NC, December 21, 2018 - The Great Internet Mersenne Prime Search (GIMPS) discovered the largest known prime number, 2 82589933 - 1, consisting of 24 863 048 digits . Volunteer Patrick Laroche's computer calculated it on December 7, 2018. Patrick is one of thousands using the free GIMPS software .
The new prime, also known as M82589933, is calculated by multiplying 82,589,933 twos and subtracting one. It surpasses the previous record prime by more than a million and a half digits in a special class of extremely rare primes known as Mersenne numbers. It is only the fifty-first open Mersenne prime; calculating each subsequent one becomes more difficult. Mersenne primes are named for the French monk Marina Mersenne , who studied these numbers over 350 years ago. Founded in 1996, GIMPS discovered the last 17 Mersenne primes. To find these primes, download the free program, and there is a chance to win a cash prize if you are lucky enough to find a new number. Professor Chris Caldwell has an authoritative website for the largest known prime numbers with a wonderful history of Mersenne primes .
Patrick Laroche is a 35-year-old IT guy living in Ocala, Florida. Patrick used GIMPS software for stress tests. He recently started looking for prime numbers to "pay back" the project. For his discovery, he received a research award of $ 3,000 from GIMPS.
Prime95 GIMPS . PrimeNet, GIMPS. PrimeNet. 3 000 50 000 , . GIMPS Electronic Frontier Foundation 150 000 , 100 000 000 .
, Prime95: , Primenet, GIMPS, . «. , . , . , . ».
Great Internet Mersenne Prime Search
Great Internet Mersenne Prime Search (GIMPS) 1996 . 1997 GIMPS « ». GIMPS , . . , , , , . GIMPS . www.mersenne.org/download/. GIMPS Mersenne Research, Inc., 501()(3). www.mersenneforum.org www.mersenne.org; .
, . , . : 2, 3, 5, 7, 11 .. , 10 , 2 5. — , 2P - 1. 3, 7, 31 127, P = 2, 3, 5 7. 50 . , 350 . , , (1588-1648 .), , P . , 300 .
GIMPS .
, . — , . 6 = 1 + 2 + 3, — 28 = 1 + 2 + 4 + 7 + 14. (1707-1783 .) , p-1: 2^(p-1)*(2^p-1). — 277232916 x (277232917-1). 49 ! , .
, GIMPS, . , , . 1990- , Apple, — . , . Fast Elliptic Encryption, Apple Computer. . , . GIMPS.
GIMPS, . , , .