An example of computational proof in the Lean program



Mathematicians have long used computers in their work as tools for complex calculations and performing routine brute-force operations. For example, in 1976, the four-color theorem was proved by the method of computer enumeration . This was the first major theorem to be proven with a computer.



Now, the proof assistant software not only verifies proofs, but helps to reach a fundamentally new level of the great unification of various mathematical fields. The concept of "condensed mathematics" promises to bring new ideas and connections between fields ranging from geometry to number theory. This is a kind of "great unification" of mathematics.



However, first things first.



The young German number theoretician Peter Scholze is called one of the most talented modern mathematicians . He boldly connects mathematics with other creative pursuits, is fond of progressive rock, puts forward unusual theories and already has experience in introducing revolutionary concepts.



Peter Scholze wants to rebuild much of modern mathematics, no less, starting with one of its cornerstones, topology. And now, thanks to a computerized theorem-proving tool called Lean, he has received the confirmation underlying his search, writes Nature.

Condensed mathematics

An ambitious plan was developed by Peter Scholze with colleague Dustin Clausen from the University of Copenhagen and presented in a lecture series on Analytical Geometry ( pdf ) in 2019 at the University of Bonn (Germany), where they work.



According to colleagues, if Scholze's plan is realized, then in 50 years teaching mathematics to graduate students may be very different from today. “I think there are many areas of mathematics that will be influenced by his ideas,” says Emily Riehl, a mathematician at Johns Hopkins University in Baltimore.



Until now, most of Scholze's "analytic geometry" has relied on a technical proof so complex that even the authors themselves were not sure of its correctness. But on June 5, 2021 Scholze announced on the blog the completion of the computer proof work!

Great unification

The defining moment of condensed mathematics is the redefinition of the concept of topology, one of the cornerstones of modern mathematics. Many objects that study mathematics have topology - this structure determines which parts of the object are close to each other and which are not. Topology gives the concept of shape, but it is more flexible than in the usual geometry: in topology, any transformation is allowed that does not break the object.



Topology plays an important role not only in geometry, but also in functional analysis, the study of functions. Functions usually "live" in spaces with an infinite number of dimensions (for example, wave functions, which are the basis of quantum mechanics). This is also important for systems of numbers called p-adic numbers, which have an exotic, "fractal" topology.



Around 2018, Scholze and Clausen began to understand that the traditional approach to the concept of topology leads to incompatibility of these three mathematical universes - geometry, functional analysis, and p-adic numbers, but you can try to eliminate these gaps.

Many results in each of the mathematical areas have analogs in other areas, although at first glance they are completely different concepts.

But if the topology is defined in the "correct" way, then the analogies between the theories will turn out to be examples of the same "condensed mathematics", writes Nature. This is a kind of "great unification" of the three areas.



Scholze and Clausen have already found "condensed" proofs of a number of deep geometric facts and can now prove theorems that were previously unknown. True, they have not yet released this data.

Theorem

Scholze detailed the essence of the task in December 2020 . He set the task of proving a very complicated theorem on the set of real numbers, which has the topology of a straight line. “It's kind of a foundational theorem that allows real numbers to enter this new structure,” Kommelin explains.







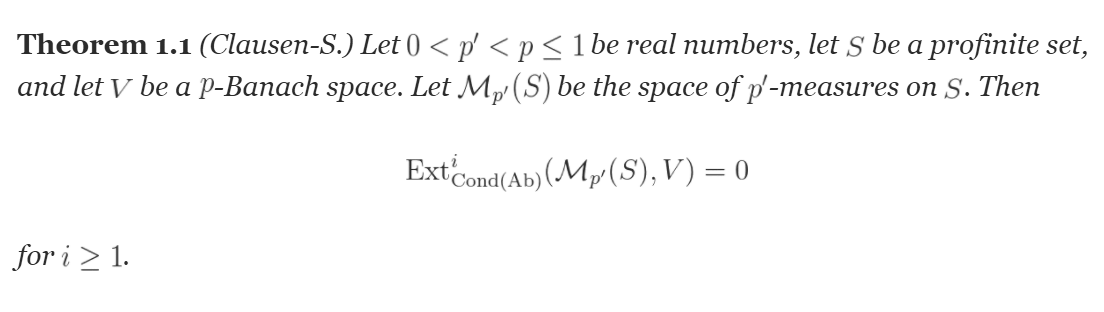
The proof work is dubbed the Liquid Tensor Experiment, after the beloved rock band of mathematicians.

Helper software for theorem proving

Proof assistant software has been around for decades. In short, the user enters statements into the system that give the machine definitions of mathematical concepts - objects - based on simpler objects that the machine already knows about. This statement can simply refer to known objects. The program will then answer whether a given fact is "obviously" true or false based on its current knowledge.



If the answer is not obvious, the user must enter more details. Thus, the auxiliary software forces the user to state the logic of their arguments in a strict form, including filling in all the blanks - simple steps that mathematicians, consciously or unconsciously, skipped.



The most famous systems of this type are Isabelle, Lean, Mizar and Coq, see a more complete list .



In this case, the mathematicians decided to use the Lean program  - and coding all the necessary concepts and objects took six months. Naturally, Scholze did not work alone. He was assisted by a group of volunteers led by Johan Kommelin, a mathematician at the University of Freiburg in Germany.





Number line, the position of numbers on it is shown $$$√2$ , $$$e$ and $$$\pi$



According to one of Johan Kommelin's assistants, the Lean version of Scholze's proof will include tens of thousands of lines of code - it is about 100 times larger than the original version: “If you just look at the Lean code, it will be very difficult for you to understand the proof, especially in its current form ". But the researchers say the effort spent getting the proof to work in the program helped them better understand the theorem and the proof.



In general, coding a theorem in an automatic proving program helps to understand that the construction of a theorem and its proof are essentially the same thing.



According to some researchers, computer programs for automatic theorem proving will soon be more widely used in universities. Perhaps computers will be able to point out some consequences or conclusions of well-known theorems that mathematicians have not noticed. Although Scholze himself says that he personally does not need such programs in the "creative work of a mathematician."



One way or another, but this case proves that theorem provers can really help in especially difficult cases. It looks like a computer is capable of simultaneously operating on more objects than a human's RAM. After the objects were introduced into the program for six months, it was still able to build a logical chain and confirm the proof.





Lean for proof of Scholze and Clausen



's theorem “These programs have their fans, but this is the first time they have played an important role in the frontier of mathematics,” says Kevin Buzzard, a mathematician at Imperial College London who was involved in a joint project to validate the results. Scholze and Clausen. - Until now, the main question hung in the air: will they cope with complex mathematics? We showed that we can handle it. "



Experts say that six months of coding in Lean is even a short time for such a monumental task. The theorem-proving software has proven that it can formally verify a highly complex original study in a reasonable amount of time.

---

Macleod VPS servers are fast and secure.



Register using the link above or by clicking on the banner and get a 10% discount for the first month of renting a server of any configuration!