Linear Algebra for Data Scientists

"Our [Irving Kaplansky and Paul Halmos] general philosophy about linear algebra is this: we think in baseless terms, write in baseless terms, but when it comes to serious business, we lock ourselves in the office and do our best with matrices."

Irving Kaplansky

.

 

, .

 

x, y ∈ ℝⁿ xᵀy

:

, . ,

.

 

x ∈ ℝᵐ, y ∈ ℝⁿ ( ) xyᵀ ∈ ℝᵐˣⁿ. , : (xyᵀ)ᵢⱼ = xᵢyⱼ,

 

A ∈ ℝⁿˣⁿ, tr(A) ( trA), : 

:

• A ∈ ℝⁿˣⁿ: trA = trAᵀ.

  
  
  
  
  

• A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.

  
  
  
  
  

• A ∈ ℝⁿˣⁿ t ∈ ℝ: tr(tA) = t trA.

  
  
  
  
  

• A,B, , AB : trAB = trBA.

  
  
  
  
  

• A,B,C, , ABC : trABC = trBCA = trCAB (  — ).

  
  
  
  
  

∥x∥ x «» . , , l₂:

, ‖x‖₂²=xᵀx.

: f : ℝn → ℝ, :

1. x ∈ ℝⁿ: f(x) ≥ 0 ().

   
   
   
   
   

2. f(x) = 0 , x = 0 ( ).

   
   
   
   
   

3. x ∈ ℝⁿ t ∈ ℝ: f(tx) = |t|f(x) ().

   
   
   
   
   

4. x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) ( )

   
   
   
   
   

 

l₁

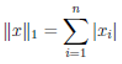
l∞

lp, p ≥ 1

, :

 

{x₁, x₂, ..., xₙ} ⊂ ℝₘ , . - , . ,

α₁,…, αₙ-₁ ∈ ℝ, , x₁, ..., xₙ



; . ,

, x₃ = −2xₙ + x₂.

A ∈ ℝᵐˣⁿ , . , ,  — A. , .

( ), A ∈ ℝᵐˣⁿ , A rank(A) rk(A); rang(A), rg(A) r(A). :

• A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). rank(A) = min(m,n), A .

  
  
  
  
  

• A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

  
  
  
  
  

• A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

  
  
  
  
  

• A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).

  
  
  
  
  

 

x, y ∈ ℝⁿ , xᵀy = 0. x ∈ ℝⁿ , ||x||₂ = 1.

U ∈ ℝⁿˣⁿ , ( ). , .

,

, , . , U (U ∈ ℝᵐˣⁿ, n < m), , UᵀU = I, UUᵀ ≠ I. , , .

, ,

x ∈ ℝⁿ U ∈ ℝⁿˣⁿ.

-

{x₁, x₂, ..., xₙ} , {x₁, ..., xₙ},

R(A) ( ) A ∈ ℝᵐˣⁿ . ,

 -, A ∈ ℝᵐˣⁿ ( N(A) ker A), , A ,

 

A ∈ ℝⁿˣⁿ x ∈ ℝⁿ xᵀ Ax. :

,

 

• A ∈ 𝕊ⁿ , x ∈ ℝⁿ xᵀAx > 0.

  
  
  
  
  

  

  ( A > 0),

  
  
  
  
  

  

  .

  
  
  
  
  

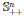
• A ∈ 𝕊ⁿ , xᵀ Ax ≥ 0.

  
  
  
  
  

  

  
  
  
  
  

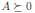
  ( A ≥ 0),

  
  
  
  
  

  

  .

  
  
  
  
  

• A ∈ 𝕊ⁿ

  
  
  
  
  

  

• , x ∈ ℝⁿ xᵀAx < 0.

  
  
  
  
  

• , A ∈ 𝕊ⁿ (

  
  
  
  
  

  

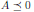
  ), x ∈ ℝⁿ xᵀAx ≤ 0.

  
  
  
  
  

• , A ∈ 𝕊ⁿ , , , x₁, x₂ ∈ ℝⁿ ,

  
  
  
  
  

  

  
  
  
  
  

  

  .

  
  
  
  
  

 

A ∈ ℝⁿˣⁿ λ ∈ ℂ x ∈ ℂⁿ ,

, A x , λ. , x ∈ ℂⁿ ∈ ℂ A(cx) = cAx = cλx = λ(cx). , cx . , , λ, 1 ( , x, –x, ).

 

---

" Data Science". , , , .

• 
  
  
  
  

---