The relationship between topography and gravity is reminiscent of the well-known chicken-and-egg problem. On the one hand, the relief undoubtedly affects the gravity force measured on its surface - the relief level determines the distance to the planet's center of mass, and the elevations of the relief contain additional attracting masses. On the other hand, the force of gravity also undoubtedly affects the relief, which is especially noticeable in the oceans, the shape of the surface of which repeats the anomalies of the force of gravity. Moreover, the surface of the relief is affected by wind and water erosion and many other factors, so that the nature of the relationship between relief and gravity becomes difficult to predict. Space images also reproduce landforms - along with the shapes and colors of vegetation and everything else in this relief, so the nature of the relationship between the images and the relief is even less obvious.
Fortunately, the gravity field and the surface relief of our planet have the property of fractality, that is, self-similarity at different scales, which is the key to determining the nature of the relationship between them.
Measurement of fractal dimension
There are many ways to define fractal dimension, and they have in common only the presence of a characteristic spatial scale. You can calculate fractality in the spatial domain, or you can also in the frequency domain (components of the spatial spectrum), differentiate and integrate ... The secret is that all the variety of methods gives similar results and the choice of a specific method is quite arbitrary, it is only important to understand how the results of the chosen calculation method compare with the results of other methods (Gneiting et al., 2012).
, , , — .
( ) , ( ) . , ( ) , , — . , , . , , , , . , . , — . , , , . , N- N+1 . , () . , (), ( , , ). ́ ́ ́ ́ . . ́ ( , ) — , (, . . , 2008).
() , . , , . () (, , 1973). () , . , 80 !
. . , , . , ( ), , ( ) (. ). , . — (, ) , . — 10 ? , . 1 1000 ( 10 … 10 ), 4 ~6000 (2πR, R ), . . — 1 , , . : ( ), . , , 5-10 (, Sentinel-1 Sentinel-2). , . , , , , , «» , .
, . , ( ) . ( - — ) . , — , . , ( , ) .
, , :
́ ( … . στάσις – ), . , ( 100–150 ) . . [ — ]
, , , (. ):
… , . . . . [ — ]
, , . 1749. 1736, , , . [ — ]
()
:
. . 1914–15 . . - 1931 . . , , , . [ — ]
, ( ), . , , (), (100%).
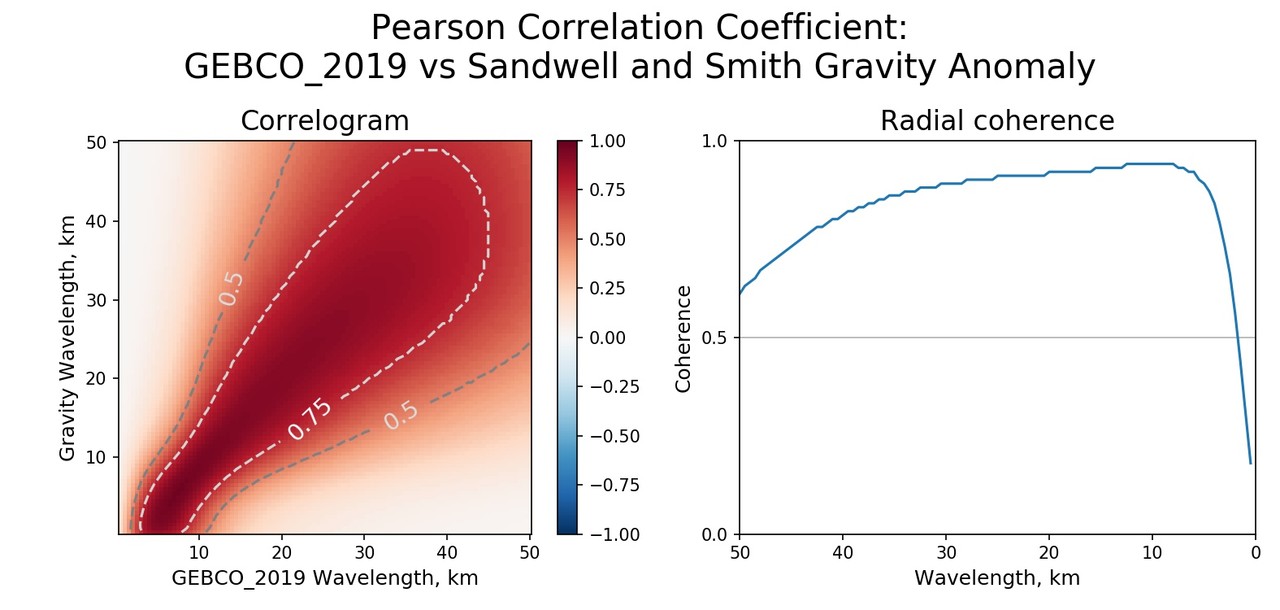
. (2.5 — 5 ). (90% ) ~15 , (75% ) ~35 , . , , , . 11 CRUST 1.0: A New Global Crustal Model at 1x1 Degrees, 15 , . 25 ( 35 ). , (), .
, :
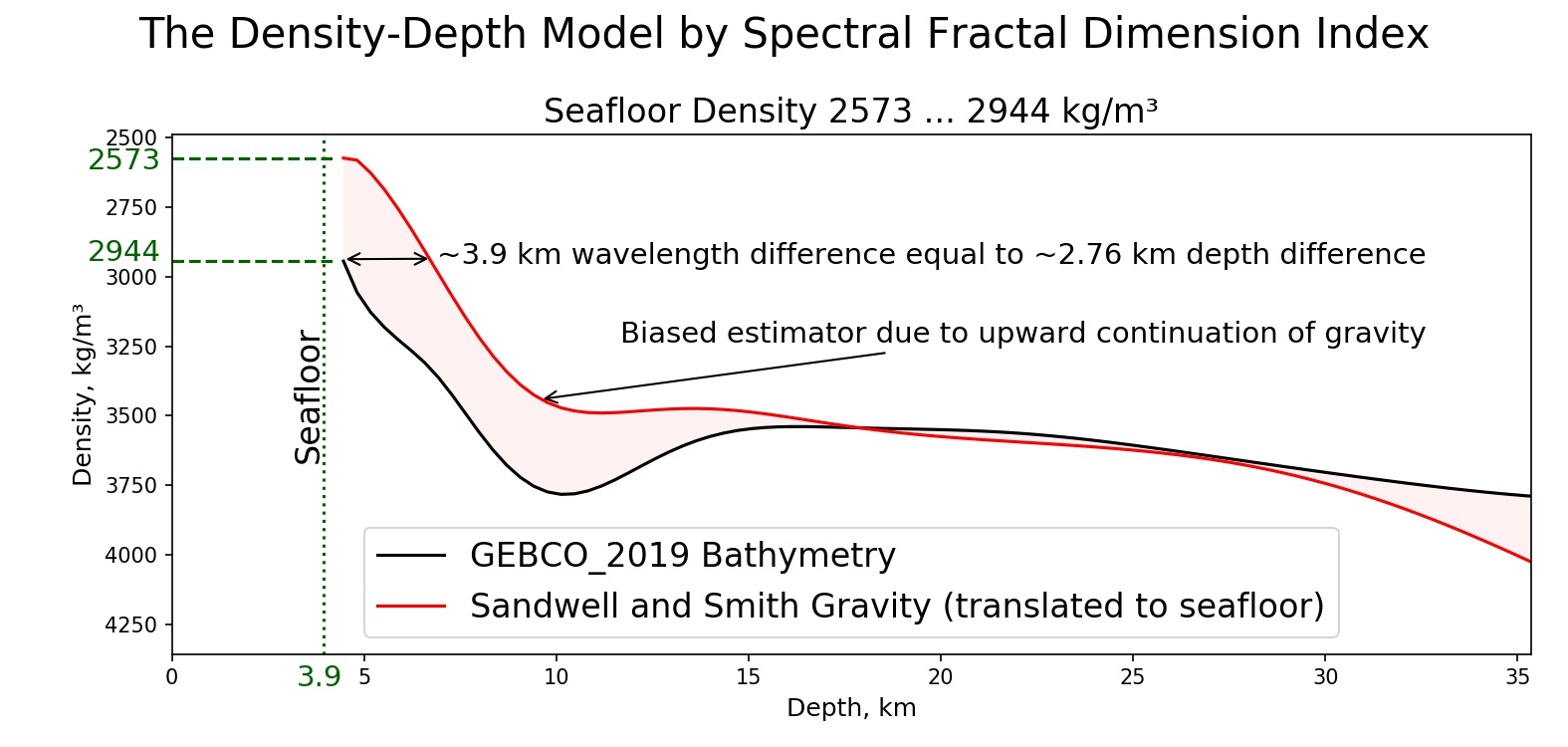
, , , . 15 35 , . , .
, , , (, ) , . , , , (). , , , . , , — , , - . , . - , . , , , .
, . , :
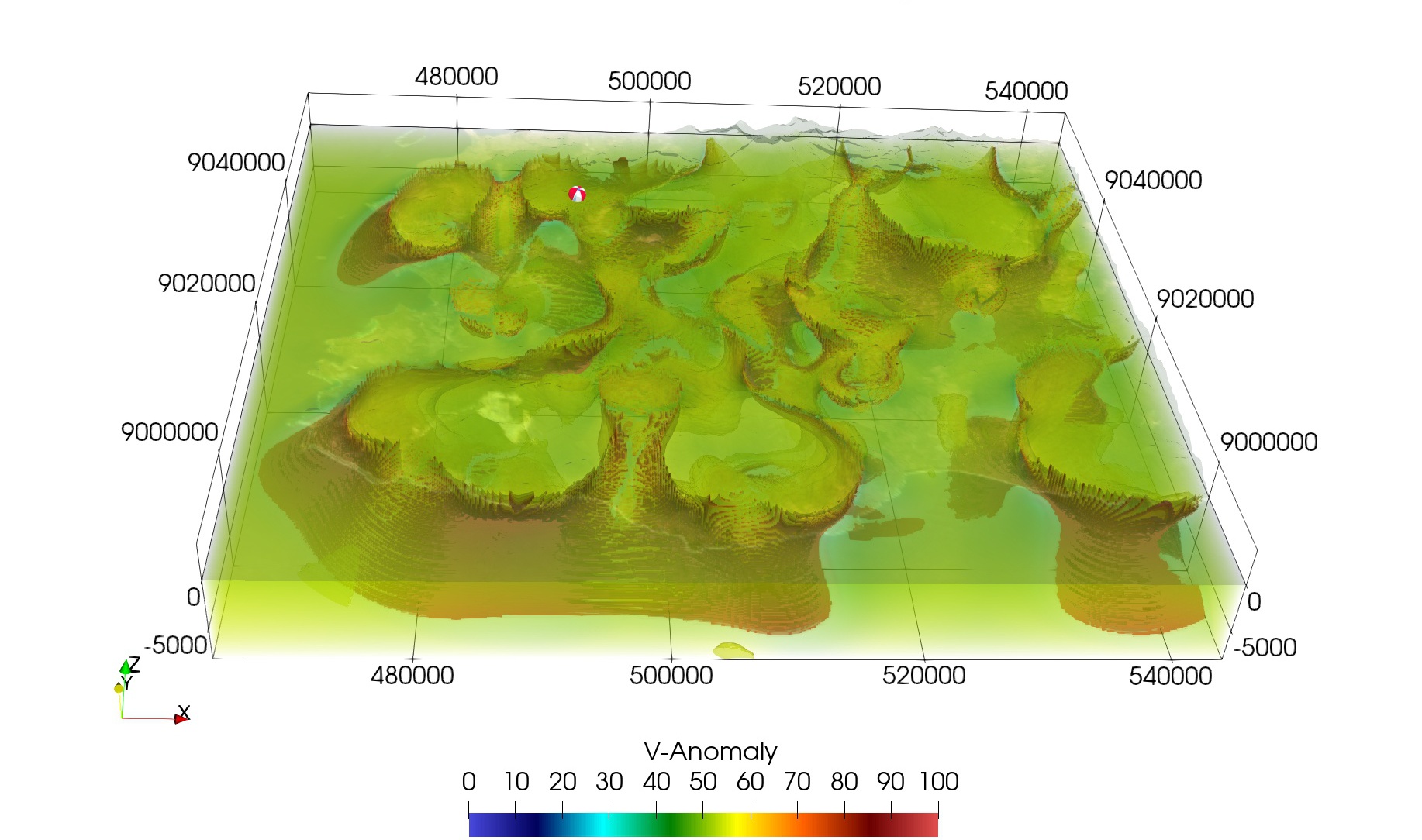
, , — . - , , , .
, , . , :

— , . , , .
, , — , .
()
, , () . , 20 , , . « », — , , , (Miranda et al., 2015). (Zhang, Featherstone, 2019) , , , .
, «» (, )? — . , , . , - , , — , , ( , , ).
,
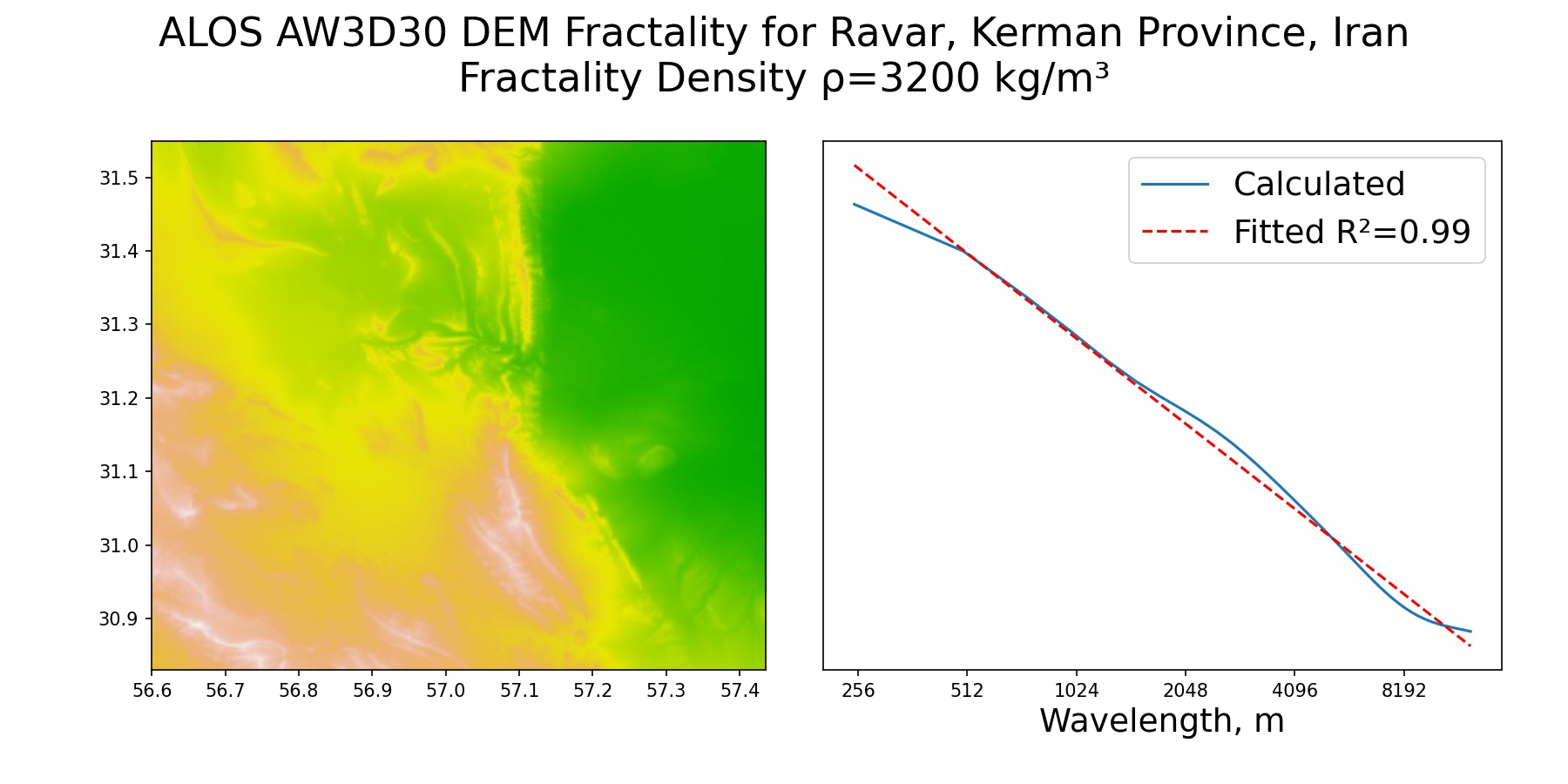
3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index , , . , , , , , . , . , , . GitHub Geological Fractality on ALOS DEM AW3D30 and Sentinel-2 SUrface Reflectance Image for Ravar, Kerman Province, Iran:
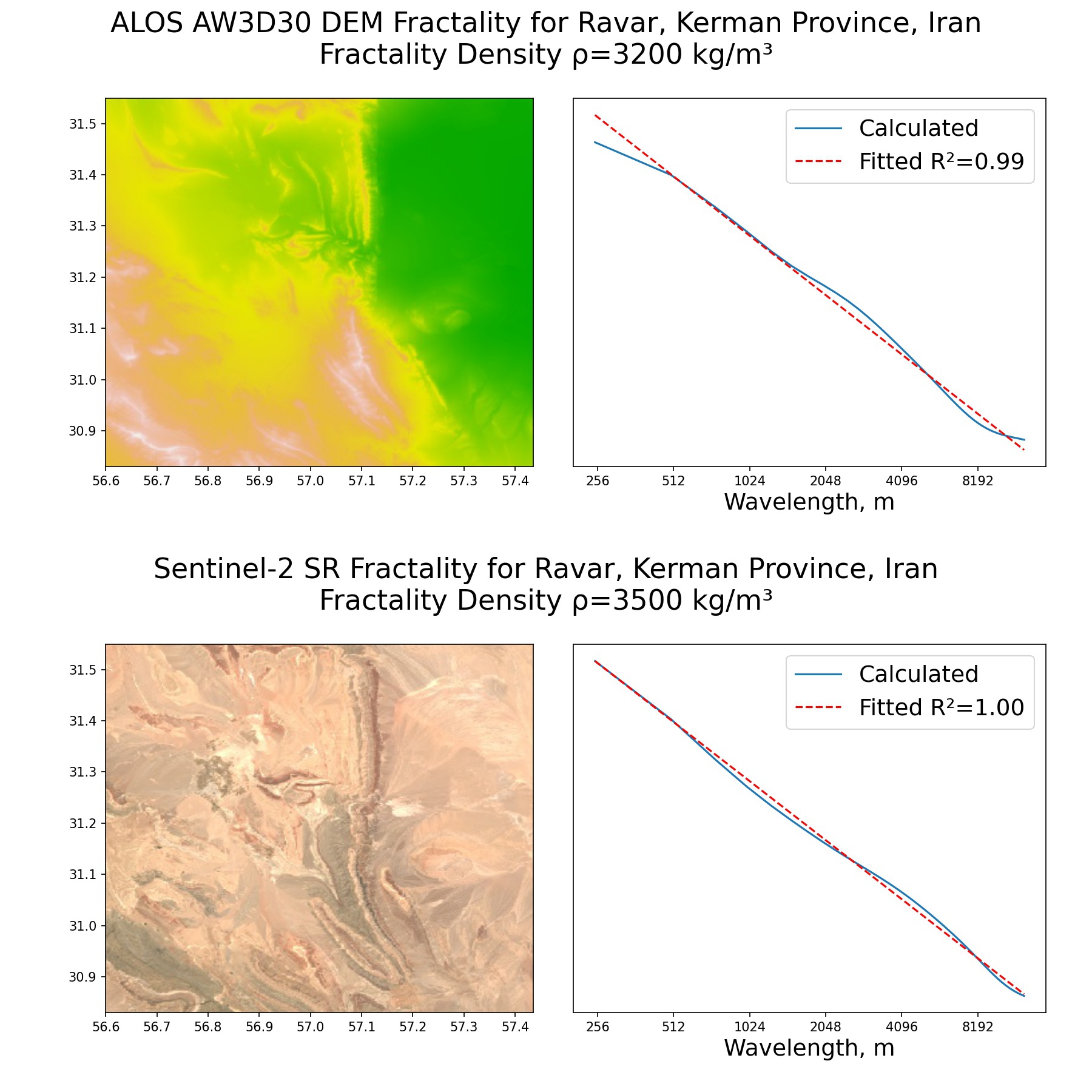
, , ρ=3200 kg/m³ R²=0.99, , . ρ=3500 kg/m³ R²=1.00, , . , , . , . . , , .
(), ! , — , , . , — , . , , , , .
, . . , . . , 1973. http://m.mathnet.ru/links/cd623304046883b7c36697e2e9f9b1d0/dan39067.pdf
, ..,1978. https://ikfia.ysn.ru/wp-content/uploads/2018/01/Malahov1978ru.pdf
, . . , . . , 2008. http://www.mathnet.ru/links/2a351947644994381a8272c4fc3ba0dd/jetpl108.pdf
Numerical simulation of the realizations and spectra of a quasi-multifractal diffusion process, A. I. Saichev & V. A. Filimonov, https://link.springer.com/article/10.1134/S0021364008090129
Gneiting, T., Ševčíková, H. & Percival, D. B. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Statist. Sci. 27, 247–277 (2012).
Zhang, K. & Featherstone, W. Exploring the Detailed Structure of the Local Earth’s Gravity Field Using Fractal and Fourier Power Spectrum Techniques. (2019).
Miranda, S. A. et al. Fractalness of land gravity data and residual isostatic anomalies map of Argentina, Chile and western Uruguay. Geofísica internacional 54, 315–322 (2015).