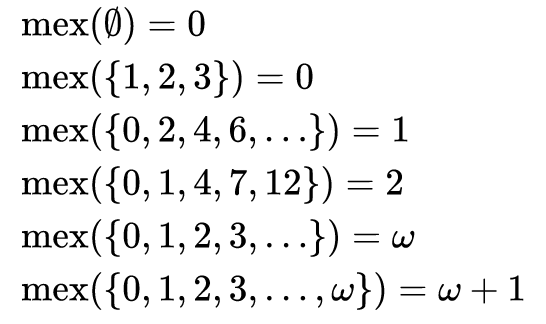
We will break down three algorithms and take a look at their performance.
Welcome under the cut
Foreword
Before starting, I would like to tell you - why did I undertake this algorithm at all?
It all started with a puzzle on OZON.

As you can see from the problem, in mathematics, the result of the MEX function on a set of numbers is the smallest value from the entire set that does not belong to this set. That is, this is the minimum value of the set of additions. The name "MEX" is shorthand for the "Minimum EXcluded" value.
And having rummaged in the net, it turned out that there is no generally accepted algorithm for finding MEX ...
There are straightforward solutions, there are options with additional arrays, graphs, but somehow all this is scattered in different corners of the Internet and there is no single normal article on this matter. So the idea was born - to write this article. In this article, we will analyze three algorithms for finding MEX and see what we get in terms of speed and memory.
The code will be in C #, but in general there will be no specific constructs.
The basic code for the checks will be like this.
static void Main(string[] args)
{
//MEX = 2
int[] values = new[] { 0, 12, 4, 7, 1 };
//MEX = 5
//int[] values = new[] { 0, 1, 2, 3, 4 };
//MEX = 24
//int[] values = new[] { 11, 10, 9, 8, 15, 14, 13, 12, 3, 2, 0, 7, 6, 5, 27, 26, 25, 4, 31, 30, 28, 19, 18, 17, 16, 23, 22, 21, 20, 43, 1, 40, 47, 46, 45, 44, 35, 33, 32, 39, 38, 37, 36, 58, 57, 56, 63, 62, 60, 51, 49, 48, 55, 53, 52, 75, 73, 72, 79, 77, 67, 66, 65, 71, 70, 68, 90, 89, 88, 95, 94, 93, 92, 83, 82, 81, 80, 87, 86, 84, 107, 106, 104 };
//MEX = 1000
//int[] values = new int[1000];
//for (int i = 0; i < values.Length; i++) values[i] = i;
//
int total = 0;
int mex = GetMEX(values, ref total);
Console.WriteLine($"mex: {mex}, total: {total}");
Console.ReadKey();
}
And one more point in the article, I often mention the word "array", although "set" would be more correct, then I want to apologize in advance to those who will be cut off by this assumption.
Note 1 based on comments : Many found fault with O (n), they say all algorithms are O (n) and don't care that "O" is different everywhere and does not actually compare the number of iterations. Then, for peace of mind, we change O to T. Where T is a more or less understandable operation: check or assignment. So, as I understand it, it will be easier for everyone.
Note 2 based on comments : we are considering the case when the original set is NOT ordered. Sorting these sets also takes time.
1) Decision in the forehead
How do we find the "minimum missing number"? The easiest option is to make a counter and iterate over the array until we find a number equal to the counter.
static int GetMEX(int[] values, ref int total)
{
for (int mex = 0; mex < values.Length; mex++)
{
bool notFound = true;
for (int i = 0; i < values.Length; i++)
{
total++;
if (values[i] == mex)
{
notFound = false;
break;
}
}
if (notFound)
{
return mex;
}
}
return values.Length;
}
}
The most basic case. The complexity of the algorithm is T (n * cell (n / 2)) ... for the case {0, 1, 2, 3, 4} we will need to iterate over all the numbers since make 15 operations. And for a completely complete row of 100 with 5050 operations ... So-so performance.
2) Screening
The second most complex implementation option fits into T (n) ... Well, or almost T (n), mathematicians are cunning and do not take into account data preparation ... For, at least, we need to know the maximum number in the set.
From the point of view of mathematics, it looks like this.
A bit array S of length m is taken (where m is the length of array V) filled with 0. And in one pass the original set (V) in array (S) is set to 1. After that, in one pass, we find the first empty value. All values greater than m can be simply ignored. if the array contains "not enough" values up to m, then it will obviously be less than the length of m.
static int GetMEX(int[] values, ref int total)
{
bool[] sieve = new bool[values.Length];
for (int i = 0; i < values.Length; i++)
{
total++;
var intdex = values[i];
if (intdex < values.Length)
{
sieve[intdex] = true;
}
}
for (int i = 0; i < sieve.Length; i++)
{
total++;
if (!sieve[i])
{
return i;
}
}
return values.Length;
}
Because "Mathematicians" are cunning people. Then they say that there is only one pass through the original array for the algorithm T (n) ... They
sit and rejoice that such a cool algorithm has been invented, but the truth is.
First, you need to go through the original array and mark this value in the array S T1 (n).
Second, you need to go through the array S and find the first available cell T2 (n) there
. all operations in general are not complicated, all calculations can be simplified to T (n * 2)
But this is clearly better than a straightforward solution ... Let's check on our test data:
- For case {0, 12, 4, 7, 1}: Forehead : 11 iterations, sifting : 8 iterations
- { 0, 1, 2, 3, 4 }: : 15 , : 10
- { 11,…}: : 441 , : 108
- { 0,…,999}: : 500500 , : 2000
The fact is that if the “missing value” is a small number, then in this case, a head-on decision turns out to be faster, because does not require triple traversing the array. But in general, at large dimensions it clearly loses to sieving, which is not really surprising.
From the point of view of the "mathematician" - the algorithm is ready, and it is great, but from the point of view of the "programmer" - it is terrible because of the amount of RAM wasted, and the final pass to find the first empty value obviously wants to be accelerated.
Let's do this and optimize the code.
static int GetMEX(int[] values, ref int total)
{
var max = values.Length;
var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];
ulong one = 1;
for (int i = 0; i < values.Length; i++)
{
total++;
var intdex = values[i];
if (intdex < values.Length)
{
sieve[values[i] / size] |= (one << (values[i] % size));
}
}
var maxInblock = ulong.MaxValue;
for (int i = 0; i < sieve.Length; i++)
{
total++;
if (sieve[i] != maxInblock)
{
total--;
for (int j = 0; j < size; j++)
{
total++;
if ((sieve[i] & (one << j)) == 0)
{
return i * size + j;
}
}
}
}
return values.Length;
}
What have we done here. First, the amount of RAM that is needed has been reduced by 64 times.
var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];
As a result, the sieve algorithm gives us the following result:
- For case {0, 12, 4, 7, 1}: screening : 8 iterations, optimization screening : 8 iterations
- For case {0, 1, 2, 3, 4}: screening : 10 iterations, optimization screening : 11 iterations
- For case {11, ...}: sifting : 108 iterations, sifting with optimization : 108 iterations
- For the case {0, ..., 999}: screening : 2000 iterations, screening with optimization : 1056 iterations
So, what's the bottom line in speed theory?
We turned T (n * 3) into T (n * 2) + T (n / 64) as a whole, slightly increased the speed, and even reduced the amount of RAM by as much as 64 times. What well)
3) Sorting
As you might guess, the easiest way to find a missing element in a set is to have a sorted set.
The fastest sorting algorithm is "quicksort", which has a complexity of T1 (n log (n)). And in total, we get the theoretical complexity for finding MEX in T1 (n log (n)) + T2 (n)
static int GetMEX(int[] values, ref int total)
{
total = values.Length * (int)Math.Log(values.Length);
values = values.OrderBy(x => x).ToArray();
for (int i = 0; i < values.Length - 1; i++)
{
total++;
if (values[i] + 1 != values[i + 1])
{
return values[i] + 1;
}
}
return values.Length;
}
Gorgeous. Nothing extra.
Check the number of iterations
- For case {0, 12, 4, 7, 1}: sifting with optimization : 8, sorting : ~ 7 iterations
- For case {0, 1, 2, 3, 4}: sifting with optimization : 11 iterations, sorting : ~ 9 iterations
- { 11,…}: : 108 , : ~356
- { 0,…,999}: : 1056 , : ~6999
These are average values and are not entirely fair. But in general: sorting does not require additional memory and clearly allows you to simplify the last step in the iteration.
Note : values.OrderBy (x => x) .ToArray () - yes, I know that memory has been allocated here, but if you do it wisely, you can change the array, not copy it ...
So I had an idea to optimize quicksort for search MEX. I did not find this version of the algorithm on the Internet, neither from the point of view of mathematics, and even more so from the point of view of programming. Then we will write the code from 0 on the way, coming up with how it will look: D
But first, let's remember how quicksort works in general. I would give a link, but there is actually no normal explanation of quicksort on the fingers, it seems that the authors of the manuals themselves understand the algorithm while talking about it ...
So this is what quicksort is:
We have an unordered array {0, 12, 4, 7 , 1}
We need a "random number", but it is better to take any of the array - this is called the reference number (T).
And two pointers: L1 - looks at the first element of the array, L2 looks at the last element of the array.
0, 12, 4, 7, 1
L1 = 0, L2 = 1, T = 1 (T took the last ones stupid)
First stage of iteration :
Until we work only with the L1 pointer.
Shift it along the array to the right until we find a number greater than our reference.
In our case, L1 is equal to 8. The
second stage of the iteration :
Now we shift the L2 pointer.
Shift it along the array to the left until we find a number less than or equal to our reference.
In this case, L2 is 1. Since I took the reference number equal to the extreme element of the array, and looked at L2 there too.
The third stage of the iteration :
Change the numbers in the L1 and L2 pointers, do not move the pointers.
And we pass to the first stage of the iteration.
We repeat these steps until the L1 and L2 pointers are equal, not their values, but pointers. Those. they must point to one item.
After the pointers converge on some element, both parts of the array will still not be sorted, but for sure, on one side of the "merged pointers (L1 and L2)" there will be elements that are less than T, and on the other, more than T. Namely this fact allows us to split the array into two independent groups, which can be sorted in different streams in further iterations.
An article on the wiki, if I do not understand what is written
Let's write Quicksort
static void Quicksort(int[] values, int l1, int l2, int t, ref int total)
{
var index = QuicksortSub(values, l1, l2, t, ref total);
if (l1 < index)
{
Quicksort(values, l1, index - 1, values[index - 1], ref total);
}
if (index < l2)
{
Quicksort(values, index, l2, values[l2], ref total);
}
}
static int QuicksortSub(int[] values, int l1, int l2, int t, ref int total)
{
for (; l1 < l2; l1++)
{
total++;
if (t < values[l1])
{
total--;
for (; l1 <= l2; l2--)
{
total++;
if (l1 == l2)
{
return l2;
}
if (values[l2] <= t)
{
values[l1] = values[l1] ^ values[l2];
values[l2] = values[l1] ^ values[l2];
values[l1] = values[l1] ^ values[l2];
break;
}
}
}
}
return l2;
}
Let's check the real number of iterations:
- { 0, 12, 4, 7, 1 }: : 8, : 11
- { 0, 1, 2, 3, 4 }: : 11 , : 14
- { 11,…}: : 108 , : 1520
- { 0,…,999}: : 1056 , : 500499
Let's try to reflect on the following. The array {0, 4, 1, 2, 3} has no missing elements, and its length is 5. That is, it turns out that an array in which there are no missing elements is equal to the length of the array - 1. That is, m = {0, 4, 1, 2, 3}, Length (m) == Max (m) + 1. And the most important thing in this moment is that this condition is true if the values in the array are rearranged. And the important thing is that this condition can be extended to parts of the array. Namely, like this:
{0, 4, 1, 2, 3, 12, 10, 11, 14} knowing that on the left side of the array all the numbers are less than a certain reference number, for example 5, and on the right, everything that is larger is not it makes sense to look for the minimum number on the left.
Those. if we know for sure that in one of the parts there are no elements greater than a certain value, then this missing number itself must be searched for in the second part of the array. In general, this is how the binary search algorithm works.
As a result, I got the idea to simplify quicksort for MEX searches by combining it with binary search. Let me tell you right away that we will not need to completely sort the entire array, only those parts in which we will search.
As a result, we get the code
static int GetMEX(int[] values, ref int total)
{
return QuicksortMEX(values, 0, values.Length - 1, values[values.Length - 1], ref total);
}
static int QuicksortMEX(int[] values, int l1, int l2, int t, ref int total)
{
if (l1 == l2)
{
return l1;
}
int max = -1;
var index = QuicksortMEXSub(values, l1, l2, t, ref max, ref total);
if (index < max + 1)
{
return QuicksortMEX(values, l1, index - 1, values[index - 1], ref total);
}
if (index == values.Length - 1)
{
return index + 1;
}
return QuicksortMEX(values, index, l2, values[l2], ref total);
}
static int QuicksortMEXSub(int[] values, int l1, int l2, int t, ref int max, ref int total)
{
for (; l1 < l2; l1++)
{
total++;
if (values[l1] < t && max < values[l1])
{
max = values[l1];
}
if (t < values[l1])
{
total--;
for (; l1 <= l2; l2--)
{
total++;
if (values[l2] == t && max < values[l2])
{
max = values[l2];
}
if (l1 == l2)
{
return l2;
}
if (values[l2] <= t)
{
values[l1] = values[l1] ^ values[l2];
values[l2] = values[l1] ^ values[l2];
values[l1] = values[l1] ^ values[l2];
break;
}
}
}
}
return l2;
}
Check the number of iterations
- For case {0, 12, 4, 7, 1}: sifting with optimization : 8, MEX sort : 8 iterations
- { 0, 1, 2, 3, 4 }: : 11 , MEX: 4
- { 11,…}: : 108 , MEX: 1353
- { 0,…,999}: : 1056 , MEX: 999
We got different MEX search options. Which one is better is up to you.
Generally. I most like screening , and here are the reasons:
He has a very predictable execution time. Moreover, this algorithm can be easily used in multi-threaded mode. Those. split the array into parts and run each part in a separate thread:
for (int i = minIndexThread; i < maxIndexThread; i++)
sieve[values[i] / size] |= (one << (values[i] % size));
The only thing you need is lock when writing sieve [values [i] / size] . And one more thing - the algorithm is ideal for unloading data from the database. You can load in packs of 1000 pieces, for example, in each stream and it will still work.
But if we have a severe memory shortage, then MEX sorting clearly looks better.
PS
I started my story with a competition for OZON in which I tried to participate, making a "preliminary version" of the sifting algorithm, I never received a prize for it, OZON considered it unsatisfactory ... For what reasons - he never confessed ... And the winner's code I haven't seen either. Can anyone have any ideas on how to solve the MEX search problem better?