This is the story of how I tried to win a game of chess with my brother. Just one fucking game. What's so special about it? Am I good at chess? Not at all. Did I learn anything while playing? Also no. Maybe this is a story about a journey for the sake of a journey, not a goal? Not really. Did I even enjoy it? Not sure.
This is a story about my attempt to be original in one of the most studied games in the world, using software development experience where it may not be needed.
Despite my absolute stupidity in chess and the complete uselessness of this article for those who seek to improve their game, I still think it was worth sharing an original way of applying engineering principles to a problem. Am I successful? You will learn about this at the end.
Why I even got involved with chess
During the 2020 pandemic, my brother, like many other people, became addicted to online chess. After playing for a couple of months, he began to talk very inspiredly about this game and challenge other family members. Our father answered the call (although he suffered a digital fiasco), but I did not give in. One of the limiting factors was my reluctance to dive into a potentially very time consuming hobby. I knew enough about this game to realize that becoming even an intermediate player requires spending hundreds if not thousands of hours playing it. Although I admit that at the same time I was also not inspired by the idea of losing to my brother, who at that time had already played more than one hundred games. I am not one.
Yet one day I succumbed to his challenge. Needless to say, the loss was devastating. I knew the rules and fundamentals of the game, since I played a little as a child, but this in no way could be compared with the skills of my brother. Later, looking at the analysis of the game at chess.com , I saw that my tactical lag only grew, move by move, until it reached the mark of +9 (which is equal to losing a rook, bishop and pawn against the absence of enemy losses). At that moment, having lost all hope, I gave up. A similar situation was repeated for a couple of more games, when I realized that something needs to be done about this.
My first decision was to delve deeper into the game.
Attempt one: study
My first attempt at improving the quality of the game was the obvious: turn to Reddit and YouTube for recommendations from other students. In between lessons from GM Naroditsky , reading and solving problems on Lichess, I also played a few games with random opponents on the Internet. Despite all this, my rating remained low (1300 - 1400 Rapid on Lichess).

After a couple more games against my brother, it dawned on me that I had no chance of winning. I continued to follow all the same development methods (playing, studying techniques and watching videos), but devoted much less time to this than my brother. At that time, he was already playing hundreds of games a month, while I was no more than 10. At this rate, my lag was growing more and more.
It was then that I realized a very important nuance: I was not particularly interested in the game itself, and, in fact, I did not want to improve in it. The main goal for me was just to defeat one person - my brother.
Attempt two: studying the enemy
A chess game is generally divided into three phases: opening , middlegame and endgame . After learning some basic mating patterns, it is usually "easy" to go from a big advantage to a win in the endgame stage, so getting that advantage was the first question for me.
In the middlegame stage, the advantage is usually achieved by deploying a long-term strategy and applying tactics . The strategy can be improved by reading and studying the principles of the game (I like that), and tactics are developed only through solving problems(which I particularly hate). Therefore, I understood that in tactical skills I would definitely lag behind, given that my brother solved about 20 such problems on chess.com every day. For me, this was an unattainable limit. Thus, there was only one opportunity left: to gain an advantage at the opening stage.
The theory behind the opening phase is enormous. At the same time, it requires memorizing long sequences and variations of moves, as well as possible answers of the opponent. Beginners don't need to memorize a lot, but some familiarity with the most typical openings can be of great benefit (or so I'm told).
Then I decided to look at some of my brother's random games and try to understand the openings he used. I also studied on Lichess debuts "Italian Party" and the Sicilian Defense , trying to remember their basic principles. Apart from that, I watched a bunch of YouTube videos.
Obviously, my brother has done all this before me (and better), so naturally I lost again. Not to mention the fact that memorizing meaningless (at least for me) opening moves is only boring and tiring. All this did not give me pleasure. Another problem was that when my opponent began to deviate from the moves prescribed in the book, I absolutely did not know how to react, because I simply did not understand the emerging positions.
It's time to step back and reflect again. Then I realized that I was actually trying not to beat my brother, but to improve my game against opponents who played the same openings perfectly. Could I have acted more directionally? Could instead have prepared specifically against his brother's weaknesses? Obviously, such an approach would only work against him, but it was quite consistent with my goal.
Attempt three: programming
Now my task has taken on a different form: to find positions at the exit from the opening, which my brother (hereinafter PlayerX) is most likely to reach, while being at a disadvantage. Please note that none of us are experts in the game, and that players of our level do not play very carefully.
The only way to counter a good player is to follow the moves in the book exactly, because then you at least know that your opponent won't make any move, gaining an advantage. However, the situation changes when you are playing against a club-level player. You can take risks (that is, temporarily find yourself in a disadvantageous position) if you know that the enemy is unlikely to be able to react to this correctly, and therefore will find yourself in a difficult position.
I also had a list of over 500 games my brother played at chess.com. And since I am a programmer, it became a natural approach for me to solve this problem in an engineering way.
I started downloading the games he played using the chess.com API and dividing them into white and black games. Then I focused on the games where my brother played for black, because I felt that I had a better chance of directing the game in the direction I wanted when playing for white.
import json
import requests
def get_month_games(player, yyyy_mm):
url = 'https://api.chess.com/pub/player/{}/games/{}'
r = requests.get(url.format(player, yyyy_mm))
if not r.ok:
raise Exception('get_month_games failed')
games = json.loads(r.content)
# Format: {games: [{url, pgn}, ...]}
return games['games']
# ...
import chess.pgn
import io
import json
with open('games.json') as f:
data = json.load(f)
games = []
for game in data:
pgn = io.StringIO(game)
games.append(chess.pgn.read_game(pgn))
black_games = [g for g in games if g.headers["Black"] == "playerx"]
Then I formulated the task as follows: “Considering all the positions that PlayerX has seen, which of them will most likely be the least profitable for him at the end of the opening?”.
This time, the task was clearly defined, and the work began in a field familiar to me. I decided to do the analysis in Python, namely in the Jupyter notebook , because I did not have the goal of creating a reusable tool, and I only needed to study the available data to find one solution.
It turned out that Python already has excellent libraries for working with chess: python-chess (move generation, evaluation and visualization) and python stockfish(bindings for evaluating a chess position using the well-known Stockfish chess engine).
I converted the problem to a graph in this way: a node is a particular chess position (described in FEN notation ). An edge connects two nodes, while the target position is reachable from the initial one by an admissible move. All games have one and the same starting node: the starting position.
Then I built a graph of all the games played by PlayerX as Black, additionally marking each edge with the number of times that the corresponding move was made.
class GamesGraph():
def __init__(self):
self.graph = igraph.Graph(directed=True)
def add_move(self, start_fen, end_fen, uci):
vs = self._ensure_vertex(start_fen)
vt = self._ensure_vertex(end_fen)
try:
e = self.graph.es.find(_source=vs.index, _target=vt.index)
e["count"] += 1
except:
e = self.graph.add_edge(vs, vt)
e["uci"] = uci
e["count"] = 1
@property
def start_node(self):
return self.graph.vs.find(chess.STARTING_FEN)
def _ensure_vertex(self, fen):
try:
return self.graph.vs.find(fen)
except:
v = self.graph.add_vertex(name=fen)
v["fen"] = fen
v["turn"] = chess.Board(fen).turn
return v
As a result, we got a weighted directed graph (not a tree, because a position can be obtained by a different sequence of moves) like this (synthetic, because the real one would simply not fit here):

Here the starting position is indicated by a square knot, the color indicates whether it is white or black to move in this position.
I also wanted to get an assessment of each position in terms of white advantage, which I used Stockfish for. Given that the process of evaluating thousands of positions takes time, I decided to run it separately and created a JSON object mapping each unique FEN position to its Stockfish estimate.
from stockfish import Stockfish
stock = Stockfish(parameters={"Threads": 8})
stock.set_depth(20)
stock.set_skill_level(20)
def eval_pos(fen):
stock.set_fen_position(fen)
return stock.get_evaluation()
# fens - FEN .
for fen, node in graph.fens.items():
node.eva = eval_pos(fen)
The evaluation of the advantage was returned in centipoints or as “checkmate in X moves”, where a positive number means an advantage for white, and a negative advantage for black:
{"type":"cp", "value":12} # 12 .
{"type":"mate", "value":-3} # .
100 centipoints means an advantage over the opponent by one pawn, and 300 to one minor piece like a bishop. However, it is worth noting that Stockfish assigns a value to the pieces depending on their position, which means that it is quite possible to have an advantage of 1000 centipoints even with an equal number of pieces on the board.
I needed to map this score to something more convenient for processing, for example, numbers between 0 and 1. For this, I decided offhand that a 300+ advantage would be displayed in 1.0, and a 300+ lag in 0. In addition, any mate in X moves (even if X is 20) will be 1 or 0.
# [-1;1]
def rating(ev, fen):
val = ev["value"]
if ev["type"] == "cp":
# -300, +300. .
val = max(-300, min(300, val))
return val / 300.0
# X : max .
if val > 0: return 1.0
if val < 0: return -1.0
# , ?
b = chess.Board(fen)
return 1.0 if b.turn == chess.WHITE else -1.0
# [0;1], 0 - min, 1 - max .
def rating_black(ev, fen):
return -rating(ev, fen) * 0.5 + 0.5
Now all the information was out of place, and I had to find the nodes of the graph (i.e. positions), in which Black was in a losing position, as well as the most suitable sequence of moves to reach them. It was necessary to weigh the ribs in such a way that it became possible to easily calculate the probability of reaching a particular position. I reasoned like this:
- In each position, you can estimate the probability of making a particular move by dividing the number of passes along the corresponding edge by the total number of moves made from that position.
- Each edge will now have a weight between 0 and 1, where a higher value reflects a higher probability of traversing it from that position.
- Then the probability of passing a particular path will be the product of the probabilities of all the edges traversed.
To solve the problem using standard graph algorithms, it was necessary to transform the edge weights so that:
- They represented distance, not probability (i.e., the greater the distance, the lower the likelihood of choosing a path).
- The distance between two nodes was the sum of the weights of the edges traversed (as opposed to the product of the probabilities).
In fact, this is much easier to do than to explain. The formula is very simple:
distance(e) = -log(prob(e))
In Python, it would look like this:
def compute_edges_weight(vertex):
all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
for edge in vertex.out_edges():
prob = edge["count"] / all_count
edge["prob"] = prob
edge["weight"] = -math.log(prob)
Taking the logarithm of the probability of choosing an edge will give a negative number, because the probability is between 0 and 1. There is no need to worry about the case when the probability is zero (as a result of which the logarithm would give minus infinity), since each edge of the graph has been traversed at least once ... The lower the probability, the more negative the logarithm will turn out, which means inverting its sign will give what we need, since:
- The sum of logarithms is the logarithm of the product of their arguments
log(a) + log(b) = log(a*b)
. - The larger the result, the lower the probability that determines it.
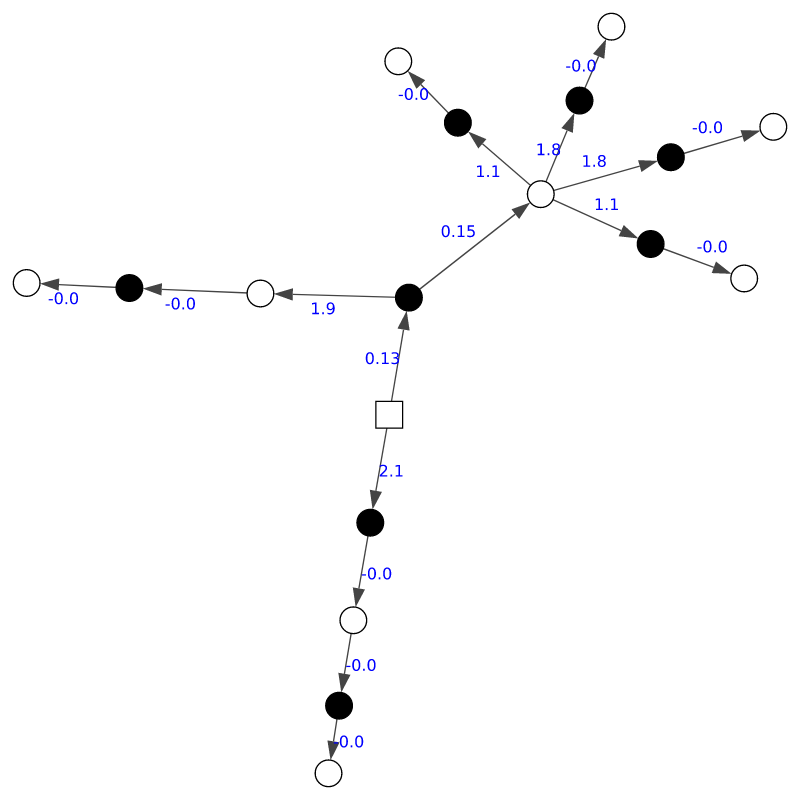
Armed with this idea, you can compute the shortest path between the start node and all other nodes using Dijkstra's algorithm . The result is a mapping between each node and the shortest path to the starting position, representing the most likely sequence of moves leading to it.
At this point, I arbitrarily chose the minimum value of the advantage and ordered the paths by probability. The first few paths represented the greatest chance for me to get out of the opening with an advantage over PlayerX.
Improvements
What have I found out? Among the positions given by this algorithm was the following (White's move):
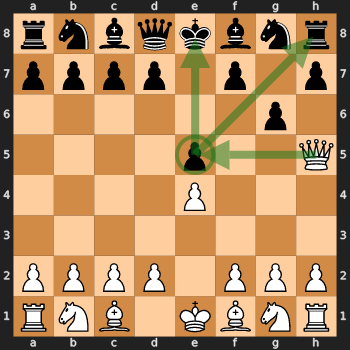
As you can see, Black is in a very awkward position (+8.9 according to Stockfish) because g6, Black's last move, was a mistake. White continues, taking the pawn from e5 and the rook. At this point, the game for Black is practically over, since he will have to save the knight, the pawn on h7 and the bishop. Another result of the algorithm was this (White's move):

Here we see a checkmate in one move ( children's checkmate ).
The problem is that PlayerX made these mistakes only a few times in its first games and did not repeat it again. Early queen attacks are usually only done by inexperienced players and are only effective against players of the same level. Having left the category of beginners, PlayerX has not made these mistakes for a long time, because more competent opponents do not go that way. I knew that such an opening would not work, because PlayerX knew how to defend against it.
Another problem was related to the sequence of moves, which occurred only once, but from typical positions. The probability of their final position was the same as the probability of the last typical position, because each edge had a probability of 1.0 (given that no other possibilities were played out). In the example below, you can follow edges 7 and 6 (the most common position on the second move), and then one of the edges with 1s. Further, all subsequent moves will be played only once (because this position was formed only in one match), as a result of which each move will have a probability of 1.0.

And here are the probabilities:

Such a scheme cannot be trusted, because it is unlikely that the same sequence of moves will be played unambiguously. For such a conclusion, we do not have enough games in which the game would take place from these positions.
The famous quote ( B. Brewster ?): "In theory there is no difference between theory and practice, but in practice there is" turned out to be correct in this case, so I needed some refinements and independent research to find more successful hypothetical positions.
I fixed the second problem by setting an upper bound on the probability of an edge so that long sequences of moves played only once would gradually lose their probability.
def compute_edges_weight(vertex, prob_ceiling=0.9):
all_count = sum(map(lambda x: x["count"], vertex.out_edges()))
for edge in vertex.out_edges():
# ... (default 90%).
prob = min(edge["count"] / all_count, prob_ceiling)
edge["prob"] = prob
edge["weight"] = -math.log(prob)
For the first problem, I just manually filtered out the bad assumptions. As a result, I had only a couple of positions left to work on.
The reason for another modification was that I did not want the probabilities of White's moves to affect the probability of choosing a path, because I played for White and could decide for myself which path to take. For this reason, I set all probabilities of White's moves to 1.0 (zero weight), resulting in a graph like this:

Preparation
In the process of studying, I chose the following position:

According to Lichess, this is the Alekhine Defense (two pawns attack). In this position, Black has only one successful move (Nb6), after which he still remains in a less advantageous position (+0.6 according to Stockfish). However, from this position PlayerX often plays Nf4, which is very unfortunate for him (+2.3). I set up a studio on Lichess and started looking at a few variations (good moves and moves played by PlayerX).
In the end, I got a tree of possibilities, which I tried to remember and understand. For example, I needed to find out what threatened a move like d5, why Nf4 was unsuccessful, and prepare optimal answers for all.
I didn’t do this for long, because I quickly got bored, and in fact I was only partially prepared.
Decisive game
It all happened as if I was looking into the future: PlayerX and I were in the position of Alekhine's defense. Finding himself in an uncomfortable situation, he missed his knight on the fifth move. It turns out that even players much more experienced than you start to make mistakes one after another when they find themselves in losing conditions. It's easy to play clearly when you win, but can you keep your cool in the opposite situation? On move 10, I was already leading with an advantage of +7.1, which makes it difficult to lose, but that was also the end of the scheme I worked out. Take a look at how cramped Black is now, and how my pieces are aiming to attack the king:

From that moment on, I started making mistakes here and there, but at the same time I managed to maintain some advantage up to move 27:
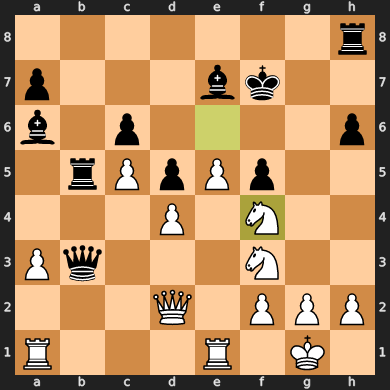
Unfortunately, I had a very limited time (we played an accelerated 10-minute game), so I had to walk quickly. In the end, I made fatal mistakes on 32 and 33 moves, and after one more I received a checkmate from my unbeaten opponent: /

Here is the whole match (with gross errors and so on):

Live batch preview: lichess.org/2qKKl2MI
conclusions
What have I learned from all this? A few things, most of which seem obvious in retrospect:
- Preparing for a specific opponent can give you a significant opening advantage.
- Novice players often miss the opportunity to take advantage of the opponent's questionable moves. In this regard, it is easy to gain an advantage by driving the enemy to a position from which there is only one coup.
- . , . .
- , , . .
- , , .
The code I used is in the repository. Note that I have not included the data there and the code itself is quite sloppy. Nevertheless, I hope it will be useful, especially for those who are still thinking about mastering computer science. Look - it is quite possible with its help to solve problems in real life, so it's not just moving bits back and forth.
That's all, friends. I hope that one day I will be able to defeat my brother, but for now I will try to achieve this ... by my own means.

