Clever Geek Handbook

How astrophysical wormholes form and how we can observe them

You can write any question or comments in the comments. I am also open for a personal dialogue in a  telegram  or a conversation in  our chat . I also have a  telegram channel  about cosmology.





Introduction

Wormholes, wormhole or wormholes (Engl .: Wormholes ) - this hypothetical space-time structure with non-trivial topology (see note 1.) Connecting one or two areas of the universe, or two different universes (see Figure 1..). The entrances to the wormhole called "mouths", and the area between the "mouths" ( mouth ) called the "throat" ( throat ). The simplest configuration of a wormhole is two mouths connected by one throat. More complex structures of molehills are also possible [1].





Translator's Note 1: A trivial topology is a topology that has the minimum possible number of open sets, i.e. empty set and all space. If we assume that there are two different universes with the topology of a sphere and connected to each other by only one wormhole, then such a space-time will have the trivial topology of a sphere. If, however, two different parts of the same universe are connected by a wormhole, then such a space-time will already have a non-trivial torus topology. If two universes with a sphere topology are connected by two or more wormholes, then the resulting space-time will also have a non-trivial topology. A system of universes connected by several wormholes,will also have a non-trivial topology.





Fig. 1: If we imagine our three-dimensional space as a two-dimensional surface, then a wormhole can be represented as a cylindrical surface connecting two regions in the same universe or two different universes. The entrances to the wormhole are called its mouths, they are connected by the throat.
.1: , , . , .

, .. , , , - , . - — .





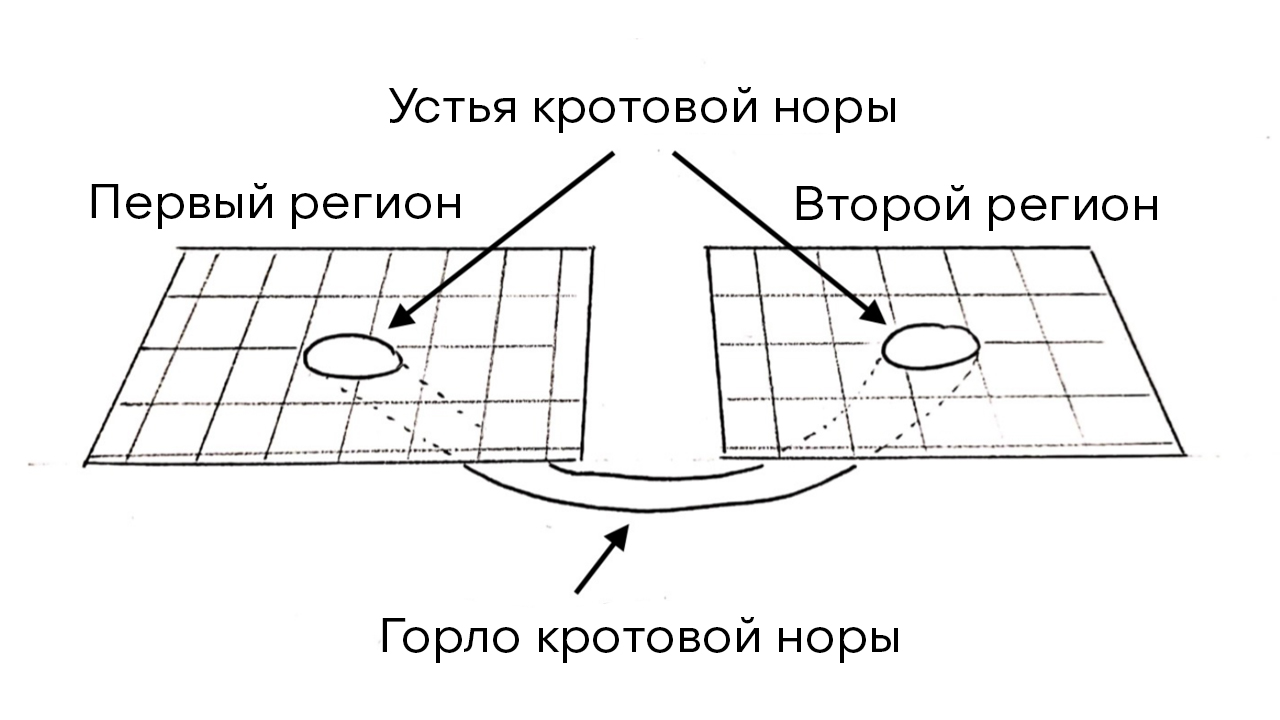
(. "..."), [2], 1957 [3]. "" "" — , , .. , . , — [6-8], , . [11-14].





, , . , , , , .





. , , .





, , . (. 2). .





2: , , , - , , .





, -

:





\ delta s ^ 2 = - \ left (1- \ frac {2GM} {r} \ right) \ delta t ^ 2 + \ frac {\ delta r ^ 2} {1- \ frac {2GM} {r}} + r ^ 2 \ delta \ Omega.

:





u ^ 2 = r - 2GM,

, . , (. . 2). , , , . , , , . , . , , , . , .





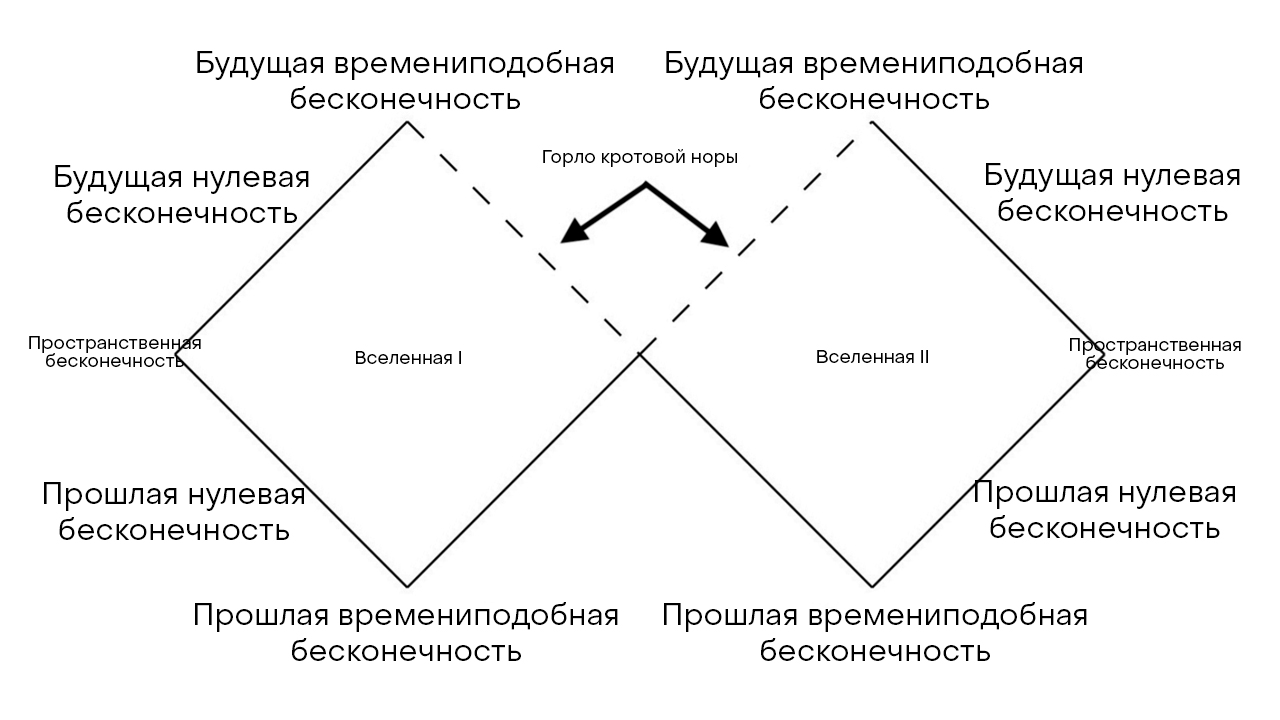
.2: -. (), (. 3). : ( .: null infinity).
.2: -. (), (. 3). : ( .: null infinity).

3: - . , , , , . — , , , ( ), , , ( ). (time-like), (null) (spatial), , .





, - . , , . , . , .





, 3+1- [27-29]. : , , , . , , , , - , . , , , , , .





, , , . , : , , , . (.: ).





.

, . [33, 34]. , -; [35].





.3: () (). ; : . [34].
.3: () (). ; : . [34].
.4: (68% 95%). . : /h, h — . [55].
.4: (68% 95%). . : /h, h — . [55].
.5: , ( « »).
.5: , ( « »).

.

, , , . ( ) .





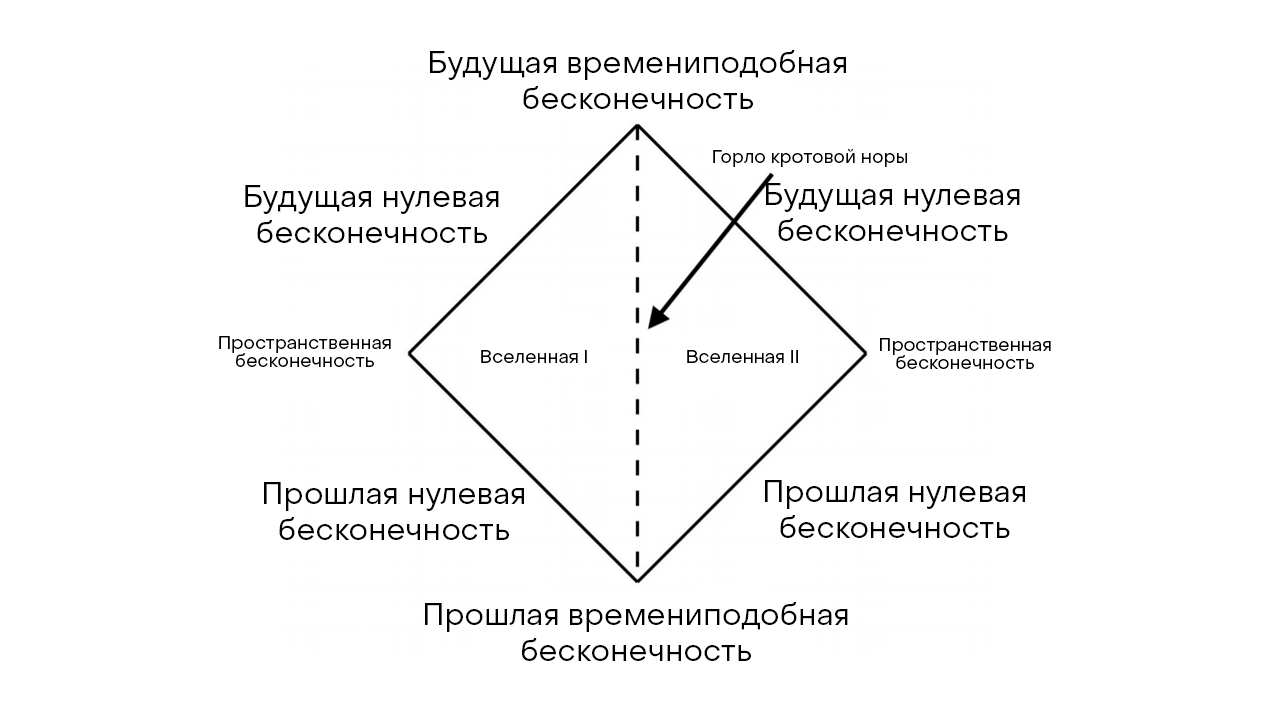
, ( ), — (.: «perturber»). - R , , .. R > rg ≡ 2GM. perturber' -:





a \approx -\mu \frac{R}{A}\frac{1}{r^2},

µ — -, A — , r — . :





\Delta a = \mu R\left(\frac{1}{r_p}-\frac{1}{r_a}\right)\frac{1}{r^2}.

, ra > rp, :





\Delta a = \mu \frac{R}{r_p}\frac{1}{r^2}.

— S2, Sgr A*, M = 4 × 106 M. S2 14M, 15,9 1031,69 . 1,5 /2 4 × 10-4 /2. , , ( , Sgr A* ) S2 . , .





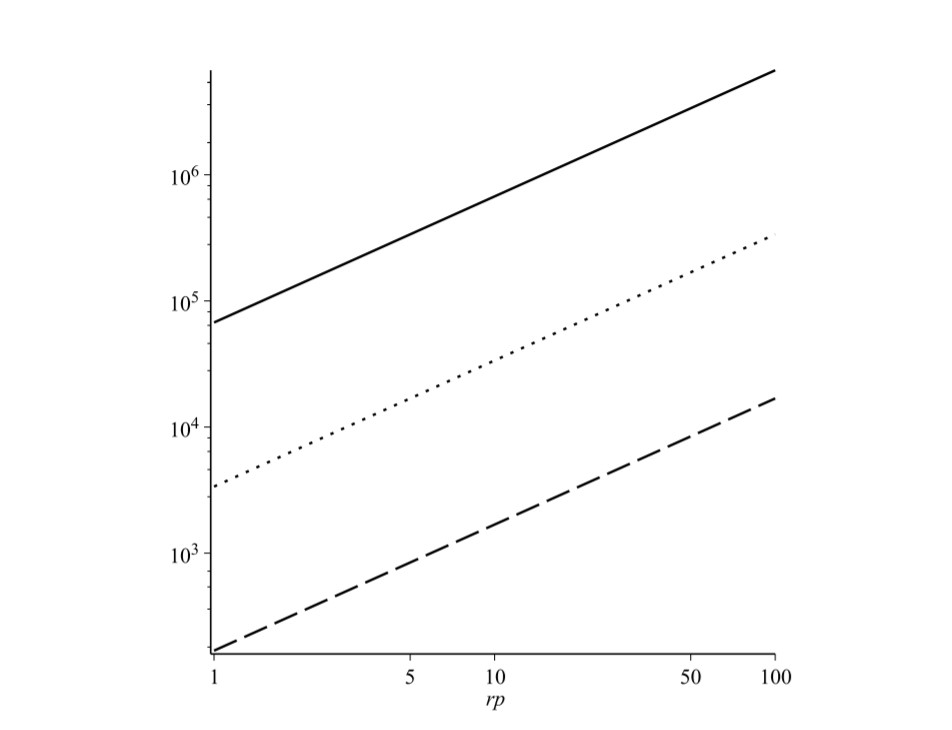
.6: µ ( , M) rp ( , 2GM) , Sgr A* S2 . S2, 4×10^−4 /*, 2×10^−5 /* 10^−6 /* .
.6: µ ( , M) rp ( , 2GM) , Sgr A* S2 . S2, 4×10^−4 /*, 2×10^−5 /* 10^−6 /* .

— . , , [62]. , , , T0. . , :





\mu > \frac{1}{G}\frac{r'_p}{r_g} r^2_{avg} \frac{1}{f'^2 T'} \sigma_{\nu} \left (\frac{T'}{\tau}\right)^{1/2},

ravg — ( ), f0 = r'p/r'a, σv — . , T0 ∝ r'p3/2 ∝ r'p1/4.





, «» , - . , R = 106 ∼ 106 rg ∼ 4 , S2 .





.

.. «» 20 [71]. - [72]. M87, Event Horizon Telescope Collaboration [16].





. - , . [73] , , - (. . 7). , , , , , .





, , , . . , ( ) [83]: - .





— , [84, 85]. . , , .





.

, . , .. , .





. 7. , . . (M ∼ 10 M) (0,1-1 ), (M ∼ 105-1010 M) — (1-100 ). .. «», (Te ∼ 100 ) . , [90].





.7: () - (). . [73].
.7: () - (). . [73].
Fig. 8: A compact object with an accreting geometrically thin and optically thick disk. The illustration is taken from [89].
.8: . [89].

[91-94]. , . -, , .. - . -, , , [95].





, , , , , , - [103].





.

- . , - , - , , .





Figure 9: Evolution of deformation, separation of a black hole and its relative velocity for event GW150914 over time. The illustration is taken from [15].
.9: , GW150914 . [15].

LIGO Virgo , . : , . , . , . . , , .





, , -. , , , [104], 5M 200M. , , , , , - ( eLISA). [105]. , - .





(KHM), [107-113]. - , KHM, .





— , . , . , . , , .





2105.00881 (gr-qc) arXiv.org 3 2021 , 8 2021 . astro-ph . : « . , , , , , . , - ». , , .





Well, I also remind you that the reader does not hesitate to ask a question or correct me in the comments. I also have a  telegram channel where I talk about the latest news in cosmology and astrophysics, as well as write about astrophotography. Write to me in a  personal  or  our chat . All good!







More articles:


All Articles