Stirring sugar in tea or coffee in the morning, you will notice that the shape of the surface of the water in the glass takes the shape of a funnel. About what this form people have been thinking about for a long time, for example, there is an article on Habré , which claims that it is a paraboloid (a parabola, if you look in a section). However, it is easy to see that this is not really a parabola. Or rather, not a parabola at all. What is it then?
In order to calculate what form the water (or other liquid) will take in the glass, it is necessary to take into account the viscosity and the effect of the glass walls. Therefore, here it is necessary to use the Navier-Stokes equations for a viscous incompressible fluid. Since the glass has a cylindrical shape, the Navier-Stokes equations must be written in cylindrical coordinates, where the z axis goes along the center of the glass and is directed upwards, and r is the distance from this axis. In general, the Navier-Stokes equations in cylindrical coordinates are as follows (Landau-Lifshitz Hydrodynamics):
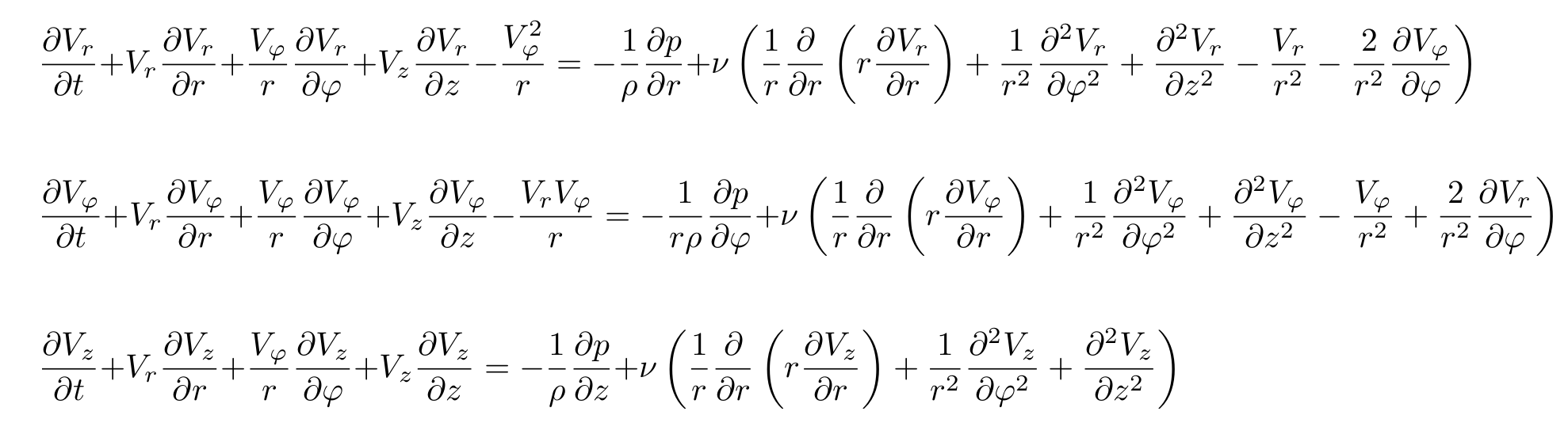
Here ro is the density of the liquid, and nu is the kinematic viscosity.
It is very difficult to solve such a system of equations in an analytical form, so we will make two reasonable simplifications. First, we will assume that the bottom of the glass does not affect the shape of the liquid, i.e. the glass is deep enough. Second, we will assume that the speed of rotation of the liquid around the circumference is much greater than the speed of movement of the liquid up and down and from the center of the glass to and from its walls. Those. these speeds can be neglected. Taking into account such simplifications, the third equation of our system will turn into identity, and the remaining two will look like this:
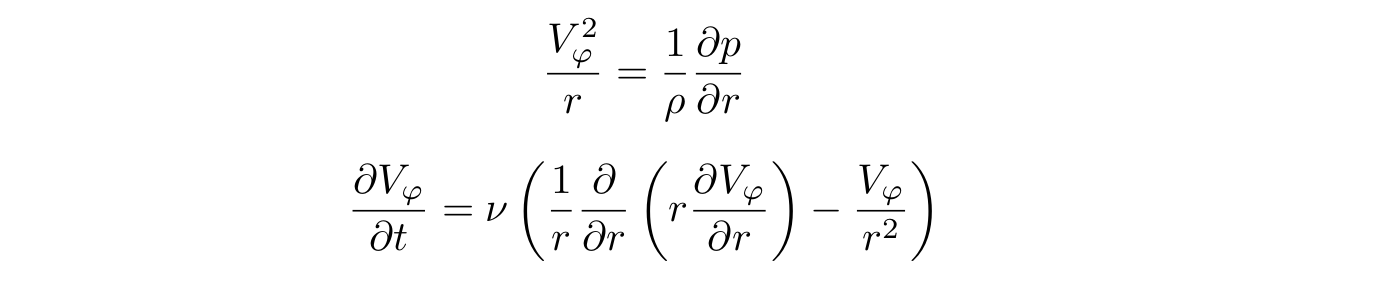
The pressure inside the liquid at any point is directly proportional to the liquid column above this point and is calculated using the well-known formula:
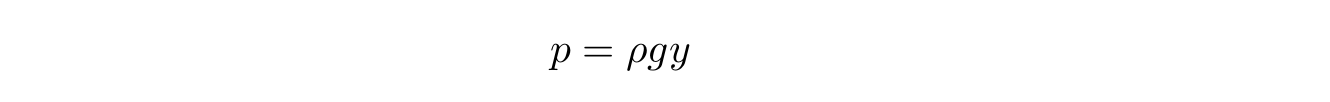
g - , y - z, , , . , :
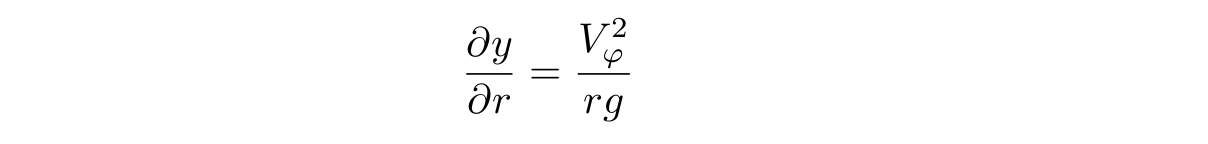
, omega , , :
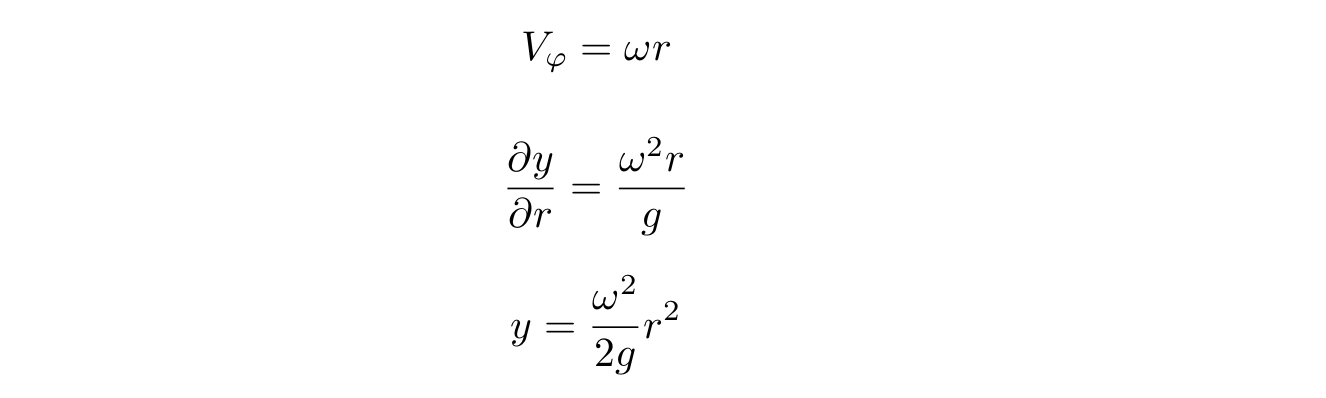
, , , , . :

, , , . , , , , :
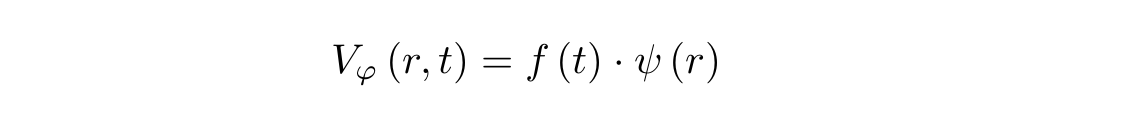
, :
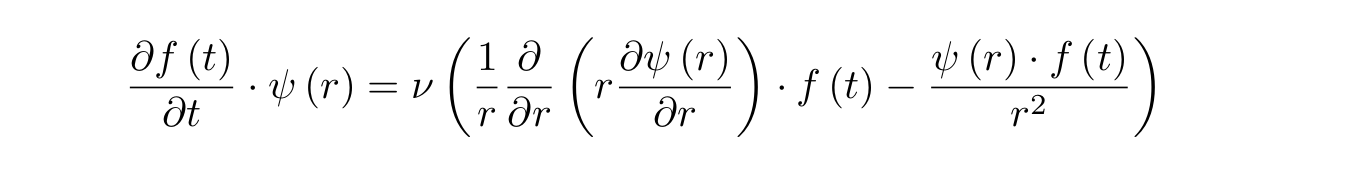
, , ,
r. , :

, r:
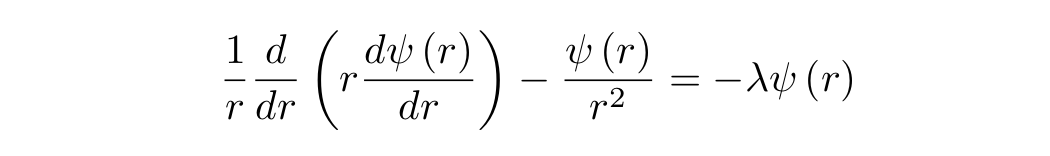
:
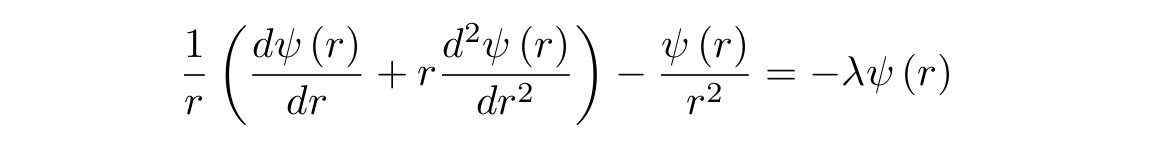
:
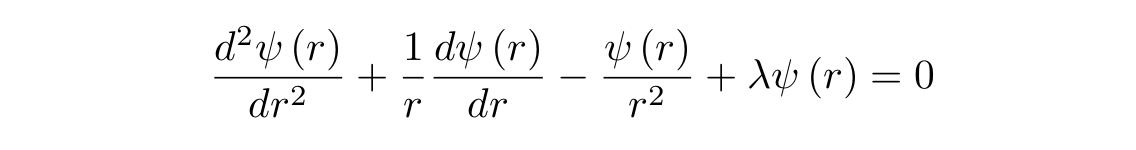
r :

, . , :
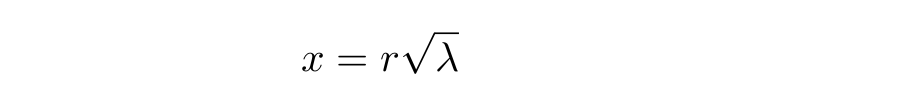
:
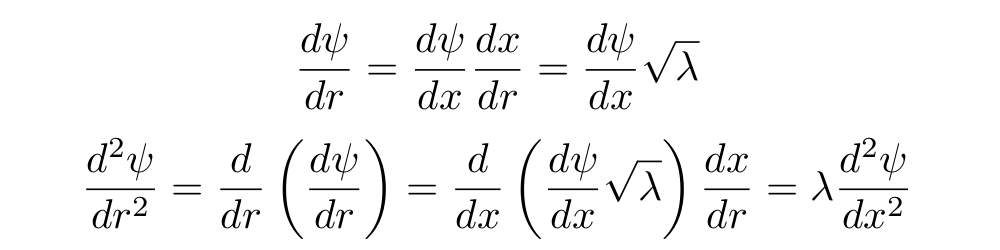
:

. , , , , , :

.

R - ,

, :
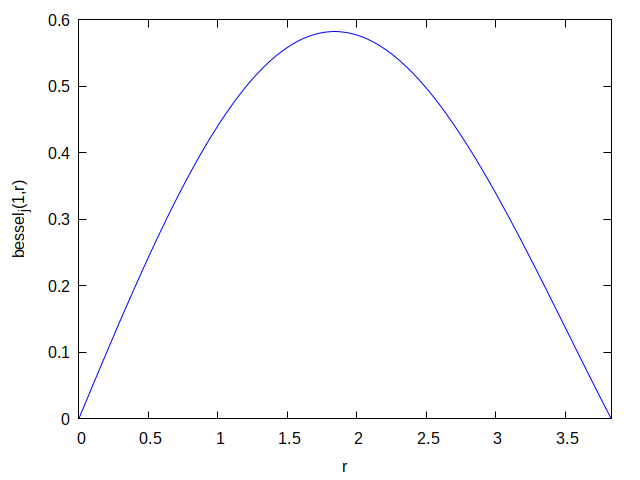
, , , :
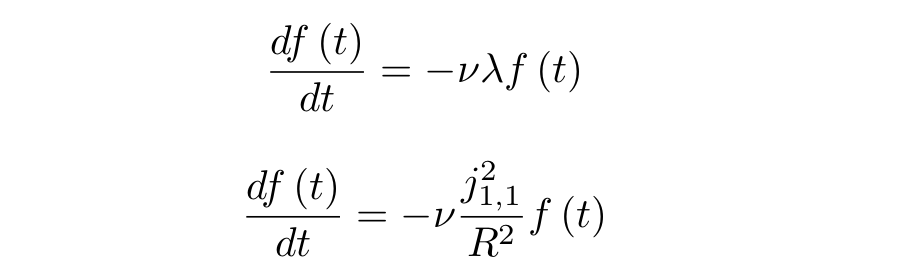
, :
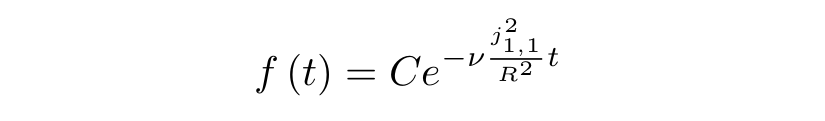
C - . , :
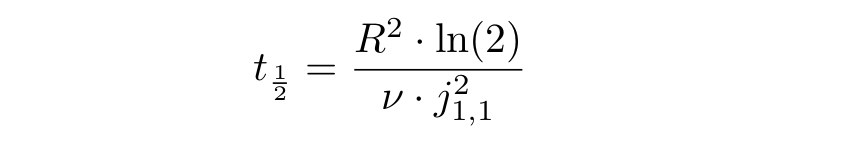
:
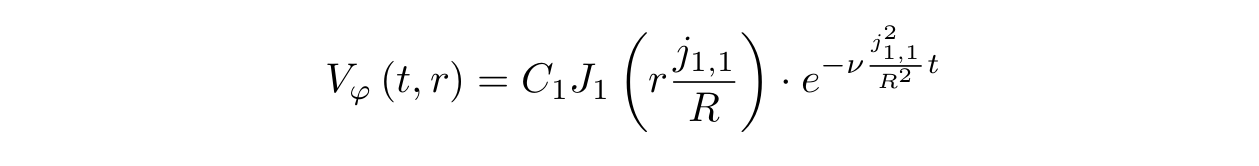
Let us now find, in fact, the shape of the surface. To do this, we substitute the tangential velocity value into the equation for y:

We integrate and get:

Here C1 and C2 are constants depending on how much we spin the liquid and on the depth of our glass. Our rotating fluid profile will look like this:

And if you represent it in 3d, then like this:

If it looks like the real form of tea you have in the morning, write in the comments.