After the publication of a series of articles on building geological models, it's time to discuss, frankly, the most interesting - how reliable are these models? Undoubtedly, all the models presented earlier are interesting and useful - earthquakes, volcanoes, gold deposits, and others. Let us now show that they are valid geological models. In fact, we have already mentioned all the evidence, but today we will discuss in detail. The theoretical part and history of the method are given in the article Computer vision methods for solving the inverse problem of geophysics , a Python notebook 3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index has been published on githubwith modeling confidence scores, and I even wrote a technical article directly about the computational methods used there Computational Geology and Visualization: A Python 3 Jupyter Notebook example , without touching on the geological implications of the computations being performed. In addition, in the article Geology of the XXI Century as the Science of Earth Data, the earthquake model is validated using the results of satellite interferometry.
Computational methods for assessing the reliability of models
, . . 3D Density Inversion by Circular Hough Transform (Focal Average) and Fractality Index : , ( ) — , — , — , . , . 1:4, 4 , — , , . , 4 64 ( ), . , .
() :

. , . , ( ) :

, , ( ), ( ). , 97.85% (Total Correlation ), 92.33% (Total Correlation ). , . 2.15% (100% — 97.85%), , . , 10-70 1.19% (100% — 98.81%):

:
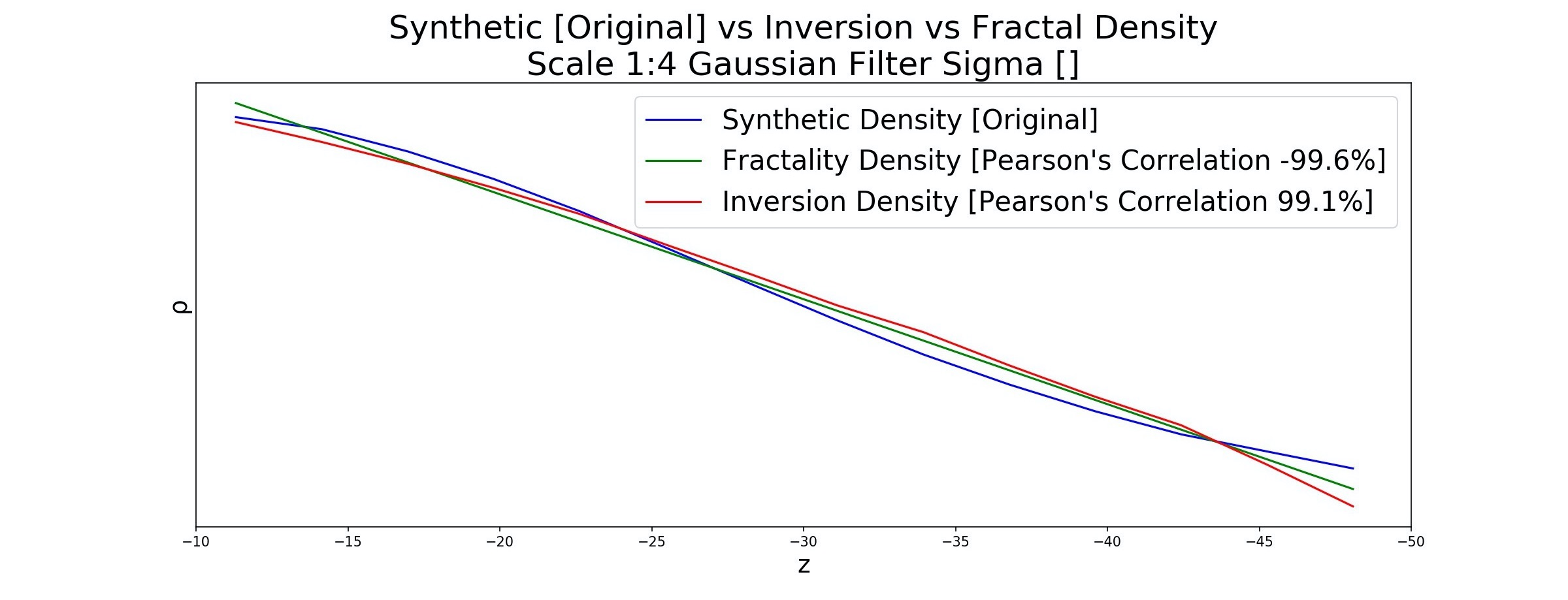
(Inversion Density) 99.1% .
, 99% . ( , 4 ) .
. ( ). , ( , ) . , . , - .
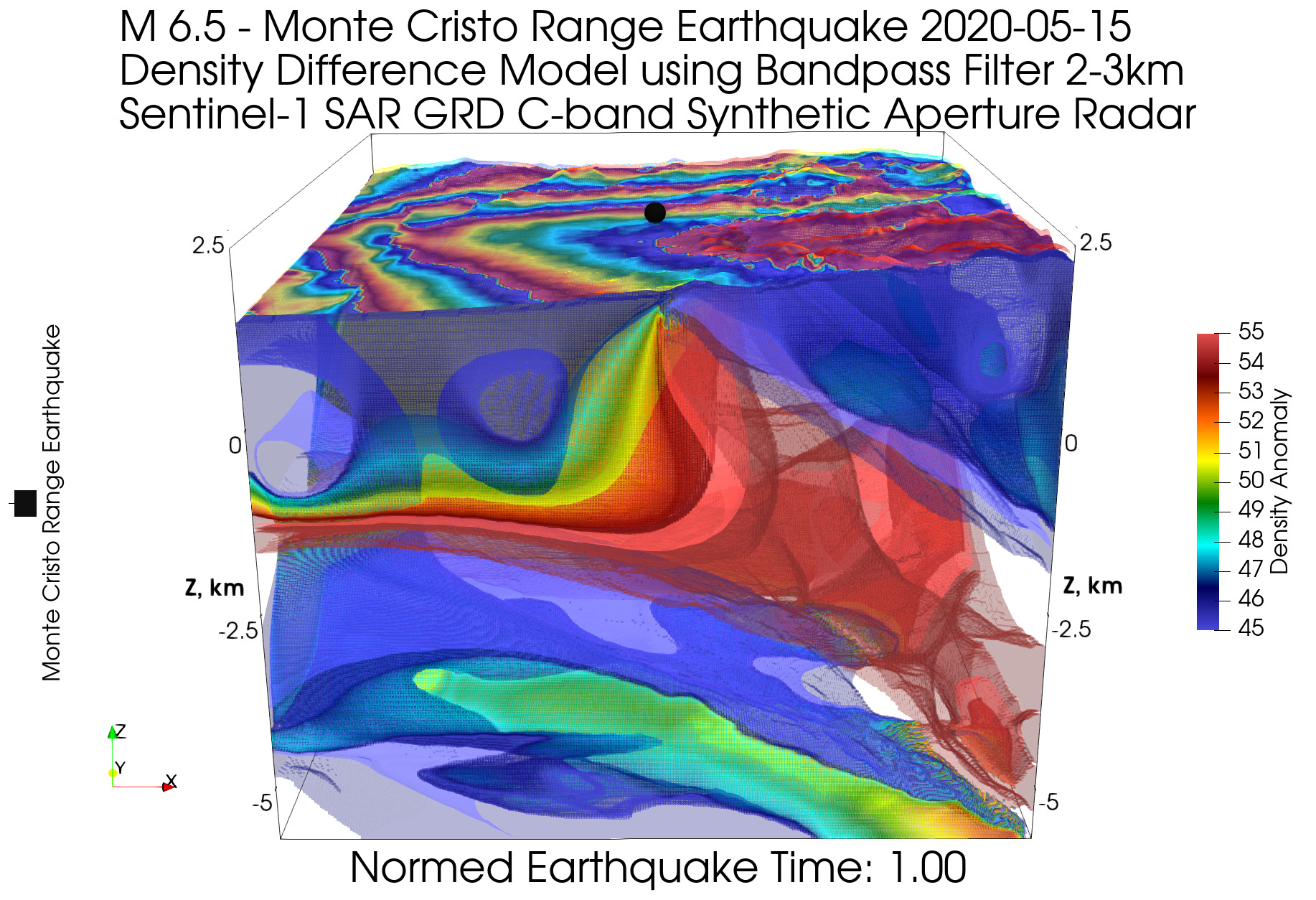
( ), XXI :
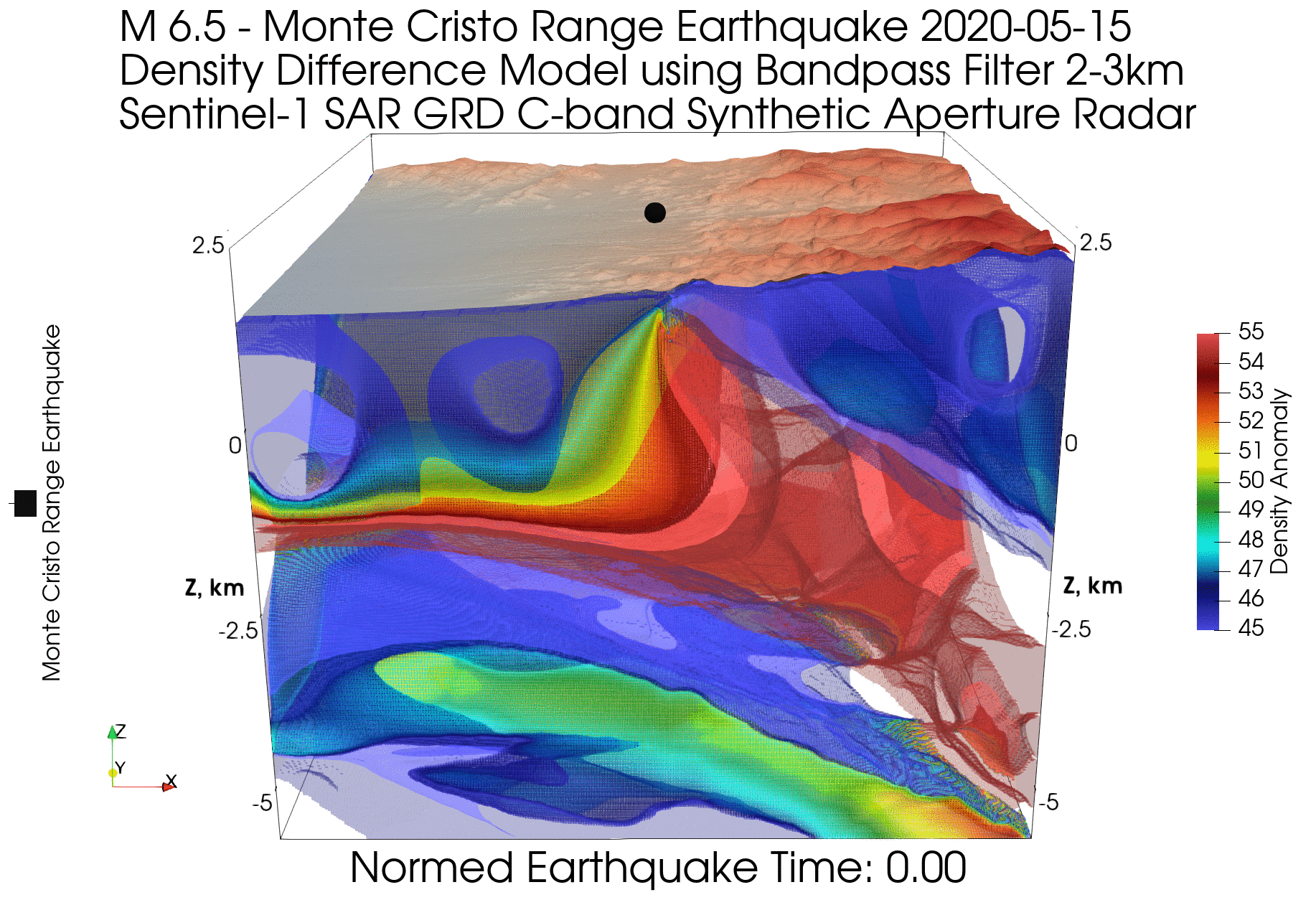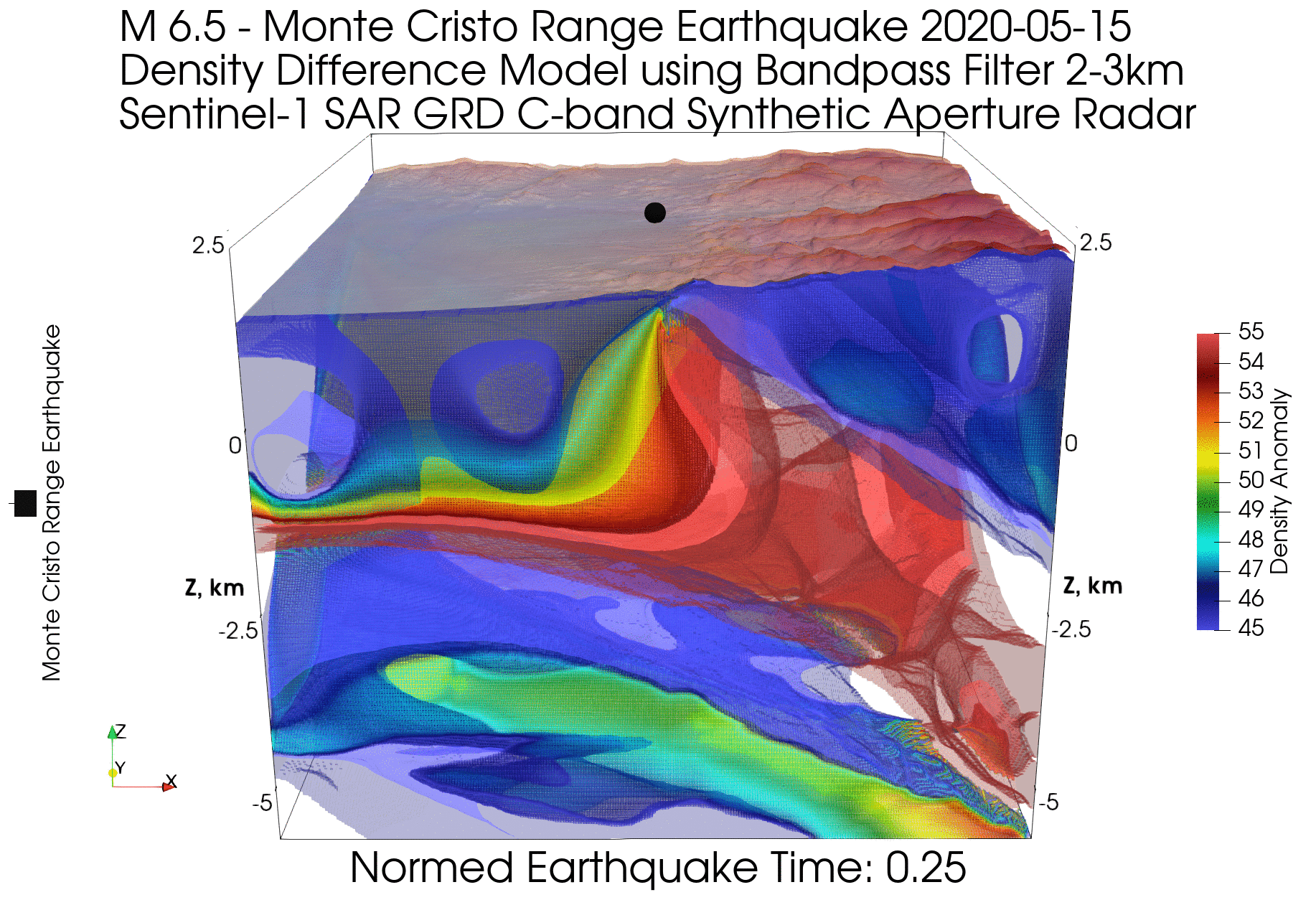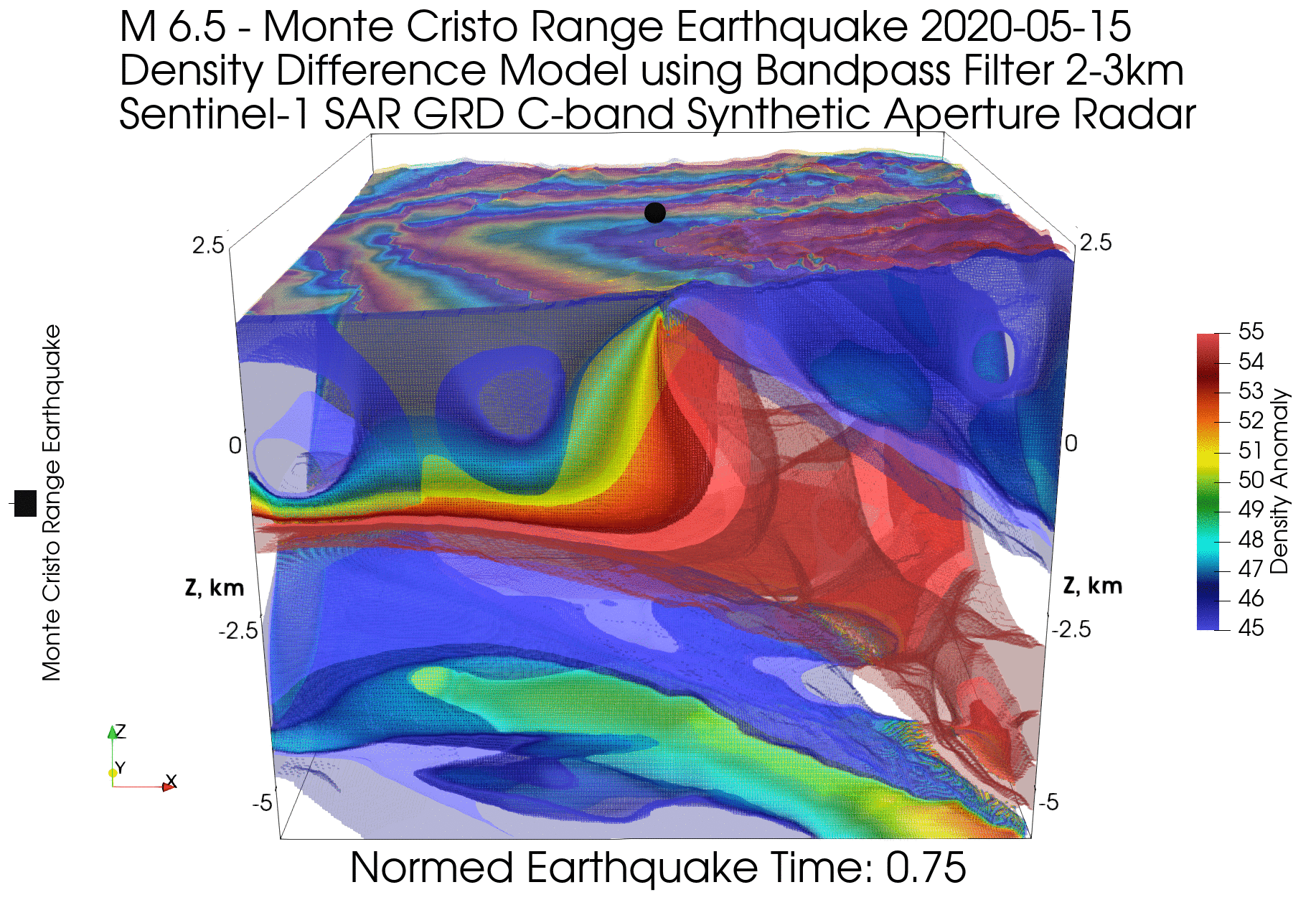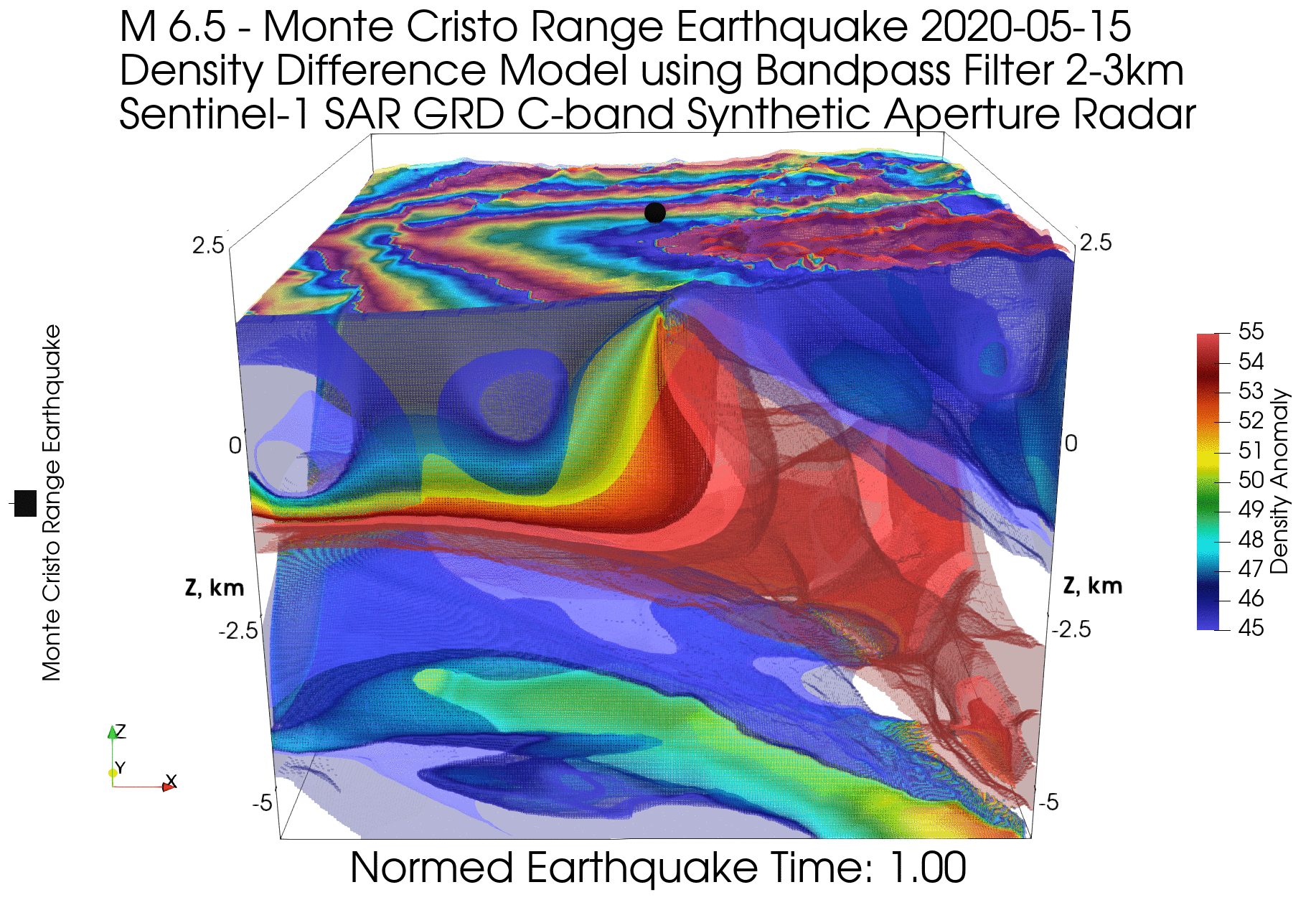
, , ( ) , . ( 2π , ). , .
:

, , . , .
, , , , . , , : ( ), «» ( ), ( , , , ). , — , .
, . (grid search) , (, , ) . , ( , ), , .
. , () , , , , , .
, , , , .