In the process of studying the basics of algorithmization and programming as a student back in the mid-2000s, I came across a fairly well-known task of filling in a "spiral" matrix. The point is, starting from position [1, 1], moving clockwise, fill a square matrix of a given value with numbers in ascending order. It took about two hours to solve it.

The filling algorithm itself was trivial, the loops, in total, consisting of N 2 iterations, assumed going through all the elements of the array in the required order, while increasing the value of the iterator by 1 and filling it with the current element of the matrix. The route started from element [1, 1], then moves horizontally to the upper right element [1, N], then down to the lower right corner [N, N], then to the lower left corner [N, 1] and ends the first circle one column below the starting point [2, 1]. Later, the same circular movement took place in the next inner circle, and so on up to the center of the matrix.
The Internet, represented by various forums, communities, sites dedicated to this area, is replete with specific solutions in various programming languages, of which mankind has invented a lot over half a century. At the same time, the mechanism for filling the matrix presented above is the main and most effective both from the point of view of a person and from the point of view of a computer (if it has a point of view).
Some time after successfully solving the problem, in the wake of re-evaluating my own abilities, I wondered: is it possible to develop a universal formula that allows, based on the size of the matrix and the coordinates of the cell, to calculate its value according to the condition of the problem - that is, ultimately fill the array, iterating over the elements " traditional "way with two nested loops from 1 to N without using a counter.
, , , , .
18 , «», «» (https://habr.com/ru/post/261773), - , .
, , .
.
( , , , , ).
, : [i, j] , . - .
: ( ) , ..
: . , .
, , , , .
1) «» «», .
2) , , , . .
3) .
: N – ().
1 . . , [1, 1] [1, N], [N, N]. , .. [2, 1].
, C++, ( , ). , , .
, 5x5 ( “a”), 1 N. .
#include <iostream>
using namespace std;
int main()
{
int N = 5; //
int a[N][N]; //
for (int ik = 0; ik < N; ik++)
for (int jk = 0; jk < N; jk++)
a[ik][jk] = 0; //
for (int ik = 0; ik < N; ik++){ // " "
for (int jk = 0; jk < N; jk++){
if (!(ik == 0 || ik == N - 1 || jk == 0 || jk == N - 1))
continue; // ""
int i = ik + 1; //
int j = jk + 1; // ( 1 N)
// ...
}
}
for (int ik = 0; ik < N; ik++){ // " "
for (int jk = 0; jk < N; jk++){
printf( "%02d ", a[ik][jk]); //
}
cout << endl;
}
return 0;
}
, , , (i + j) 1 . 2, E1,2 = 3 .. (i + j) . Xs = i + j - 1, . :
…
int Xs = (i + j – 1);
a[ik][jk] = Xs;
…
:
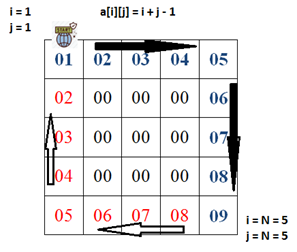
. , .
a[ik][jk] = Xs
, [5, 5] , 1.
, (i = 5, j = 4) 10. , ( N * 4 - 4 = 16 2) Xs.
a1,2 = 4N – 4 + 2 – Xs = 4N – Xs - 2.
…
int Xs = i + j - 1;
a[ik][jk] = 4 * N - Xs - 2;
…

, – .
, .
1. ai,j = Xs = i + j - 1; [1, 1] [N, N].
2. ai,j = 4*N – 2 - X; [N, N] [2, 1].
, . , - , , (y = |x|) .
, :
F1 1 i, j [1, 1] … [N, N] , – 0. , F2 , , 1 [N, N - 1] … [2, 1], 0 [1, 1] … [N, N].
switcher, i j, , .
-1, 0 / 1 . F1 F2 .
, i j, . ?
a[ik][jk].
…
int Xs = i + j - 1;
a[ik][jk] = j – i;
…

, 0, [1][1] [N][N] 0. N N. switcher.
…
int switcher = (j - i + N) / N;
a[ik][jk] = switcher; // switcher
…
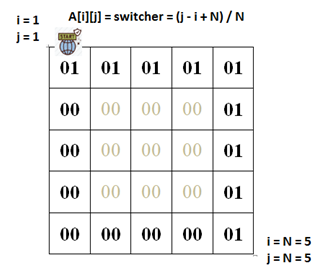
, F1 F2. F1 , , .. F1 (switcher) = switcher. F1 (switcher) * Xs [1, 1] [N, N], . , . switcher – 1, .. F2.(switcher) = |switcher – 1|.
, :
…
a[ik][jk] = switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…
:

, , .
2 . .
. , , , ? if (!(ik == 0 || ik == N - 1 || jk == 0 || jk == N - 1)) continue;

, , , , . , , . , 1, . , .
, [2, 2] 03 17, . , , « » . .. ( ) .
, . , , . , Turbo Pascal – ( ).
, :
…
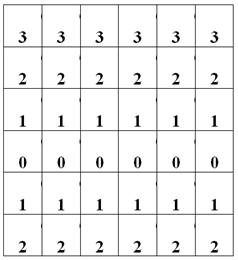
a[ik][jk] = abs(N / 2 + 1 - i);
…
, .
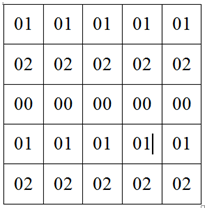
. , , .
Ic, Jc (c center).
…
Ic = abs(i - N / 2 - 1);
Jc = abs(j - N / 2 - 1);
…
, .
, - – .
… a[ik][jk] = Ic + Jc; …
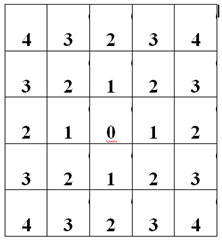
, – , . . , Ic Jc.
… a[ik][jk] = Ic - Jc; …
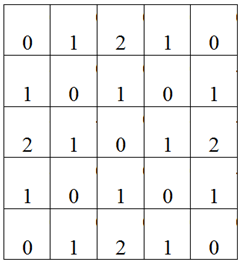
. , , .
…
a[ik][jk] = abs(Ic – Jc) + Ic + Jc;
…
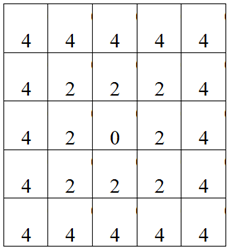
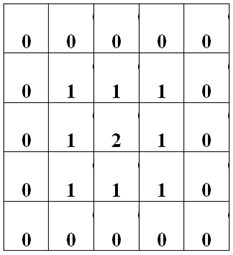
. , , . , . Ring.
…
Ring = N / 2 - (abs(Ic – Jc) + Ic + Jc) / 2;
a[ik][jk] = Ring;
…
. , N = 6 , ( , ).
N = 6

. : ? - .
, Ic Jc. N = 6, Ic = |i - N / 2 - 1|.
. , 1 3- ( ).
…
Ic = abs(i - N / 2 - 1) + (i - 1) / (N /2) * ((N-1) % 2);
…
N, .
Jc.
…
Jc = abs(j - N / 2 - 1) + (j - 1)/(N /2) * ((N-1) % 2);
…
. Ring 6.
… a[ik][jk] = Ring; …

. .
3 . . ( ).
, :
…
a[ik][jk] = switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…

: «» (.. 1), , ( [1,2] [2,2], 16 17)
, - . , – .
, Xs ( ) , .
Xs = (i – Ring) + (j – Ring) – 1.
…
a[ik][jk] = switcher * Xs + abs(switcher - 1) * (4 * N - 2 - Xs);
…

. , . , 4 * N - 2 - Xs , , N – 2 * Ring. .
:
…
a[ik][jk] = switcher * (Xs) + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs);
…

, . – , , .
, . :
Coef = N2 – (N – 2Ring)2
((a−b)2=a2−2ab+b2), 4Ring(N - Ring).
.
…
a[ik][jk] = Coef + switcher * (Xs) + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs);
…
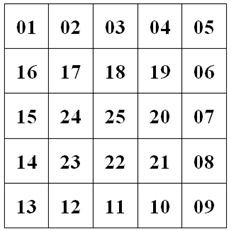
!
:
…
int switcher = (j - i + N) / N;
int Ic = abs(i - N / 2 - 1) + (i - 1)/(N /2) * ((N-1) % 2);
int Jc = abs(j - N / 2 - 1) + (j - 1)/(N /2) * ((N-1) % 2);
int Ring = N / 2 - (abs(Ic - Jc) + Ic + Jc) / 2;
int Xs = i - Ring + j - Ring - 1;
int Coef = 4 * Ring * (N - Ring);
a[ik][jk] = Coef + switcher * Xs + abs(switcher - 1) * (4 * (N - 2 * Ring) - 2 - Xs);
…
You can, of course, try to expand a single formula, replacing additional variables with expressions based only on i, j and N, and try to reduce it by mathematical methods. But believe me, I tried, it turned out to be something so inconceivable (half a page) that I decided to leave it as it is.
(PS. It does not work only for N = 1, since a division by zero error occurs. But as the saying goes, "a little bit does not count").