TLDR: tiny models have bypassed trendy graph neurons in predicting molecular properties.
Code: here . Protect the environment.
PHOTO: Anders Hellberg for Wikimedia Commons, model - Greta Thunberg
[1] (uGCN) - , , . , , — (GCN) . .
: , uGCN , , ( [2] ).
— . (uGCN + degree kernel + random forest) 54:90 GCN, 93:51, , , GCN ( — : ) . ~10 ~4 . , !
: , , , WWW .. ( ) [1].
, G=(V, E) — , , V E — e(i, j) i j. (Labeled Property Graph), xi i ( , ). [3] (GNN) — ( , , — , ), , , . , — GNN ' , '. (GCN) (https://tkipf.github.io/graph-convolutional-networks/) , , - .
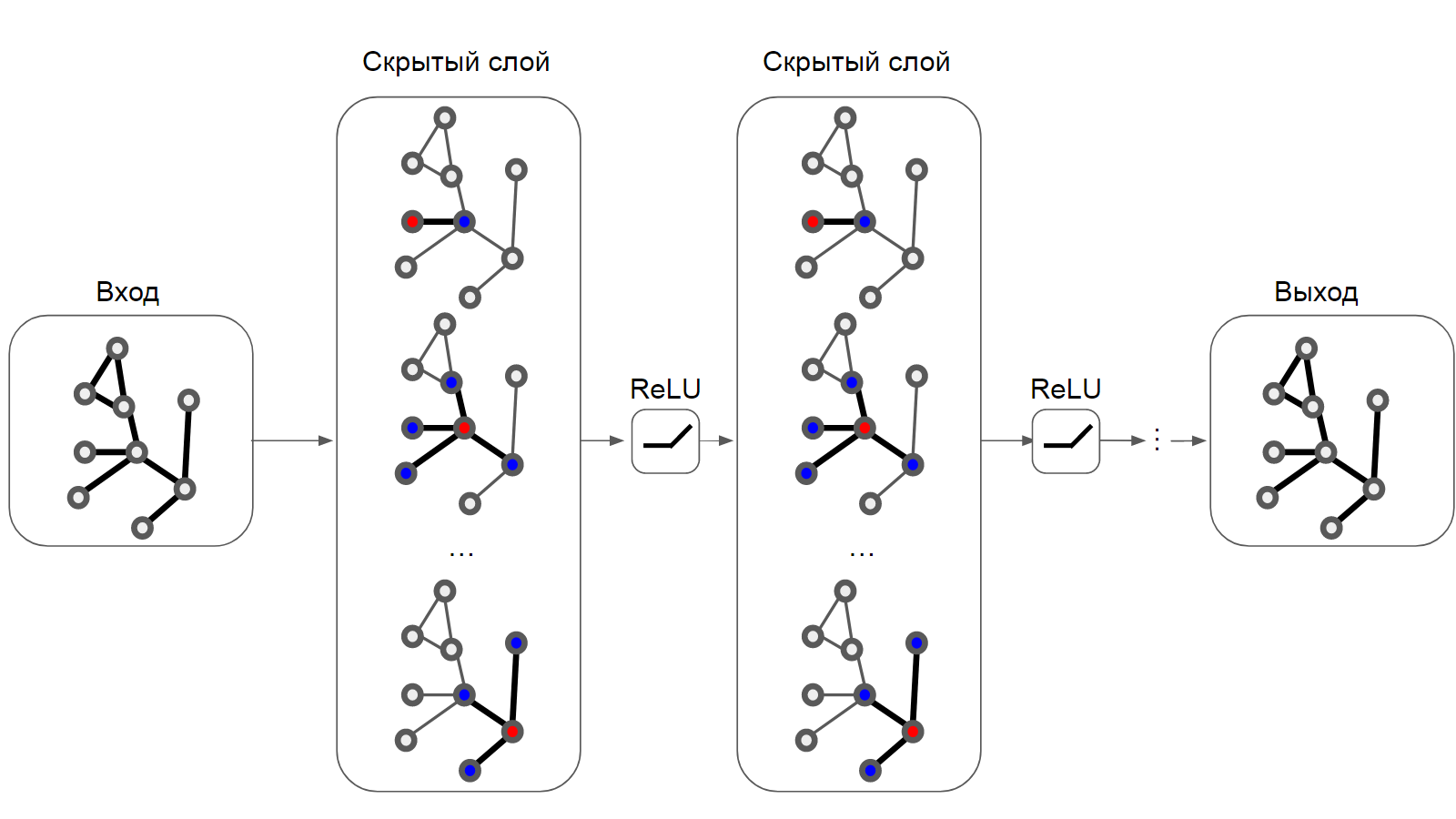
GCN .
. (i) TUDatasets [4] (ii) ( ) . (iii) .
, . : AIDS, BZR, COX2, DHFR, MUTAG PROTEINS. Pytorch Geometric [5] ( ) : [6]. 12 .
AIDS Antiviral Screen Data [7]
, . . 2000 , 1110 , , 37 .
Benzodiazepine receptor (BZR) ligands [8]
405 , — 276, 35 .
Cyclooxygenase-2 (COX-2) inhibitors [8]
467 , — 237, 35 .
Dihydrofolate reductase (DHFR) inhibitors [8]
756 , — 578, 35 .
MUTAG [9]
188 , . — 135 , 7 .
PROTEINS [10]
-. 1113 , 3 . — 975 .
!
12 .
:
(1) 80/20 Pytorch Geometric ( random seed = 42 ), 80% () , 20% — ;
(2) (accuracy) .
, , .
GCN 200 learning rate = 0.01 :
() 10 — ;
() , ( , ) — GCN ( );
(3) 1 ;
(4) .
288 : 12 12 2 .
Degree kernel (DK) — ( , ), ( , , — ).
import networkx as nx
import numpy as np
from scipy.sparse import csgraph
# g - NetworkX
numNodes = len(g.nodes)
degreeHist = nx.degree_histogram(g)
#
degreeHist = [x/numNodes for x in degreeHist]
(uGCN) — 3 (ReLU, .. f(x) = max(x, 0)). 64- ( ) . .
A = nx.convert_matrix.to_scipy_sparse_matrix(g)
, iggisv9t :
# A -
# X - (np.array)
D = sparse.csgraph.laplacian(A, normed=True)
shape1 = X.shape[1]
X = np.hstack((X, (D @ X[:, -shape1:])))
( )
.
uGCN :
# A -
# X - (np.array)
# W0, W1, W2 -
D = sparse.csgraph.laplacian(A, normed=True)
# 0
Xc = D @ X @ W0
# ReLU
Xc = Xc * (Xc>0)
#
Xn = np.hstack((X, Xc))
# 1
Xc = D @ Xn @ W1
# ReLU
Xc = Xc * (Xc>0)
Xn = np.hstack((Xn, Xc))
# 2 -
Xc = D @ Xn @ W2
# -
embedding = Xc.sum(axis=0) / Xc.shape[0]
DK uGCN (Mix) — , DK uGCN.
mix = degreeHist + list(embedding)
— 100 17 .
(GCN) — , 3 64 (ReLU), ( GCN uGCN), ( 50%) . , GCN (B) GCN-B, () GCN-A.
144 (12 * 12 ) 288 :
147:141
, .
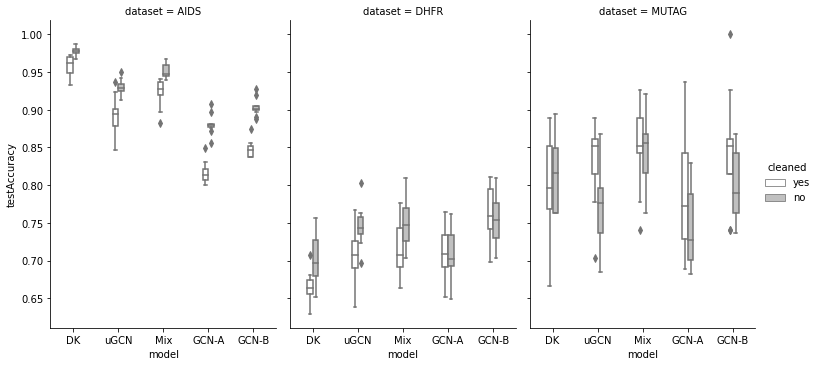
, : AIDS, DHFR(A) MUTAG.
, DK 48 AIDS, 10% ( ) GCN.
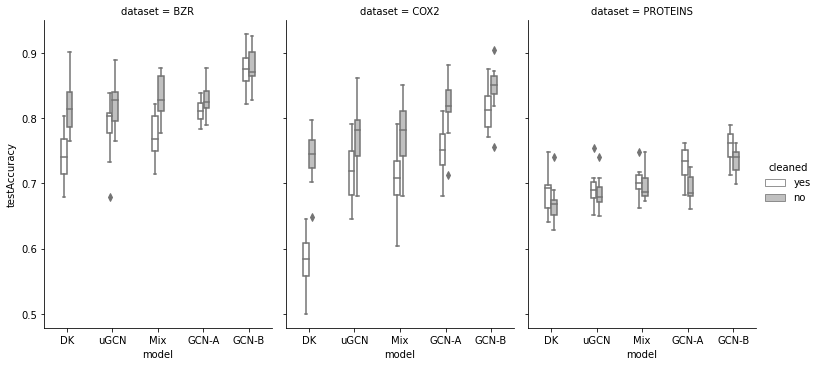
GCN: BZR, COX2 PROTEINS.
:
90 — GCN-B;
71 — DK;
55 — Mix (uGCN + DK);
51 — GCN-A;
21 — uGCN.
: DK AIDS (48 ); GCN-B BZR (12) COX2 (24) PROTEINS (24) - (B); . ----------------- Dataset: BZR, cleaned: yes Scenario: A DK 0 uGCN 3 Mix 1 GCN 8 ----------------- Dataset: BZR, cleaned: no Scenario: A DK 4 uGCN 1 Mix 4 GCN 3 ----------------- Dataset: BZR, cleaned: no Scenario: B DK 1 uGCN 0 Mix 1 GCN 10 ----------------- Dataset: COX2, cleaned: yes Scenario: A DK 0 uGCN 3 Mix 1 GCN 8 ----------------- Dataset: COX2, cleaned: no Scenario: A DK 0 uGCN 1 Mix 1 GCN 10 ----------------- Dataset: DHFR, cleaned: yes Scenario: A DK 1 uGCN 1 Mix 4 GCN 6 ----------------- Dataset: DHFR, cleaned: yes Scenario: B DK 0 uGCN 0 Mix 3 GCN 9 ----------------- Dataset: DHFR, cleaned: no Scenario: A DK 2 uGCN 4 Mix 5 GCN 1 ----------------- Dataset: DHFR, cleaned: no Scenario: B DK 0 uGCN 1 Mix 5 GCN 6 ----------------- Dataset: MUTAG, cleaned: yes Scenario: A DK 2 uGCN 3 Mix 6 GCN 1 ----------------- Dataset: MUTAG, cleaned: yes Scenario: B DK 1 uGCN 2 Mix 5 GCN 4 ----------------- Dataset: MUTAG, cleaned: no Scenario: A DK 5 uGCN 0 Mix 7 GCN 0 ----------------- Dataset: MUTAG, cleaned: no Scenario: B DK 5 uGCN 0 Mix 6 GCN 1 ----------------- Dataset: PROTEINS, cleaned: yes Scenario: A DK 2 uGCN 1 Mix 0 GCN 9 ----------------- Dataset: PROTEINS, cleaned: no Scenario: A DK 0 uGCN 1 Mix 6 GCN 5 -----------------
, — Google Spreadsheet.
, . . , .
, , , . [2] , Label Propagation . , — , , , , .
, — . Free Lunch Theorem , — . — . , , . , — …

. , : , , , — ( , ) — .
GCN , , ( ) , , . , uGCN, , GCN 2% (96 98) , - .
, . GNN [2].
, , . , ( ) . : cs224w, Open Graph Benchmark [14] [15] — . , , , — .
, . — .

[1] Kipf & Welling, Semi-Supervised Classification with Graph Convolutional Networks (2017), International Conference on Learning Representations;
[2] Huang et al., Combining Label Propagation and Simple Models out-performs Graph Neural Networks (2021), International Conference on Learning Representations;
[3] Scarselli et al., The Graph Neural Network Model (2009), IEEE Transactions on Neural Networks ( Volume: 20, Issue: 1, Jan. 2009);
[4] Morris et al.,TUDataset: A collection of benchmark datasets for learning with graphs (2020), ICML 2020 Workshop on Graph Representation Learning and Beyond;
[5] Fey & Lenssen, Fast Graph Representation Learning with PyTorch Geometric (2019), ICLR Workshop on Representation Learning on Graphs and Manifolds;
[6] Ivanov, Sviridov & Burnaev, Understanding isomorphism bias in graph data sets (2019), arXiv preprint arXiv:1910.12091;
[7] Riesen & Bunke, IAM Graph Database Repository for Graph Based Pattern Recognition and Machine Learning (2008), In: da Vitora Lobo, N. et al. (Eds.), SSPR&SPR 2008, LNCS, vol. 5342, pp. 287-297;
[8] Sutherland et al., Spline-fitting with a genetic algorithm: a method for developing classification structure-activity relationships (2003), J. Chem. Inf. Comput. Sci., 43, 1906-1915;
[9] Debnath et al., Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds (1991), J. Med. Chem. 34(2):786-797;
[10] Dobson & Doig, Distinguishing enzyme structures from non-enzymes without alignments (2003), J. Mol. Biol., 330(4):771–783;
[11] Pedregosa et al., Scikit-learn: Machine Learning in Python (2011), JMLR 12, pp. 2825-2830;
[12] Waskom, seaborn: statistical data visualization (2021), Journal of Open Source Software, 6(60), 3021;
[13] Hunter, Matplotlib: A 2D Graphics Environment (2007), Computing in Science & Engineering, vol. 9, no. 3, pp. 90-95;
[14] Hu et al., Open Graph Benchmark: Datasets for Machine Learning on Graphs (2020), arXiv preprint arXiv:2005.00687;
[15] Bronstein et al., Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges (2021), arXiv preprint arXiv:2104.13478.