, Qrator Labs @dimak24 . Core — hr@qrator.net.
1
- : , ; : -
. , , . , .
, ( 2). ( 3) , 1978 , . — . : , , , , .
2 ,
— . :
. , :
.
: -, , , . -,
. ,
100%. :
3
, : 1, 1/2, 1/4 ..:
, ?
, :
,
,
0: ,
,
.
.
.
. ,
. ,
.
. ,
, , .
, , .
:
,
. ,
!
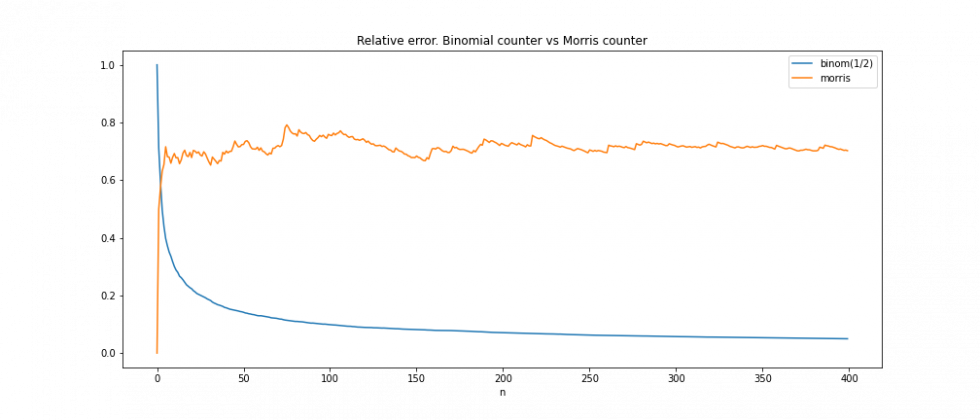

4
: , . — < > — .

, , :

5
. , , , . , . , , - . , , EMA , .
: . ,
,
. ,
!
,
:

6

:
:
, 2 ,
.
.
, ( , ). ; , .
:
,
:
:
;
.
( )
.
( ) ! , ( ):


.
. . , , , . , :

, , :

, ( ,
).
, ( )
. ,
:

7
— ! !
, ...
8
:
. :
— , . , .
,
:
, : , , ,
:
,
.., —
,
,
:
,
..,
.
,
. , ( ). — .
( , ,
):
:
, , :
[1] Morris, R.Counting large numbers of events in small registersCommunications of the ACM, 1978 21(10), 840-842.
[2] http://gregorygundersen.com/blog/2019/11/11/morris-algorithm/ −
[3] https://habr.com/ru/company/qrator/blog/334354/ − EMA-
[4] https://habr.com/ru/post/208268/ −