
Mathematics is often called the "language of science." It is well suited for quantitative processing of almost any scientific information, regardless of its content. And with the help of mathematical formalism, scientists from different fields can, to some extent, "understand" each other. Today, a similar situation is emerging with Computer Science. But if mathematics is the language of science, then CS is its Swiss knife. Indeed, it is difficult to imagine modern research without analyzing and processing huge amounts of data, complex calculations, computer modeling, visualization, and the use of special software and algorithms. Let's look at some interesting "stories" when different disciplines use CS methods to solve their problems.
Bioinformatics: from Petri dishes to biology In silico
Bioinformatics can be called one of the most striking examples of the intersection of CS and other disciplines. This science deals with the analysis of molecular biological data using computer methods. Bioinformatics as a separate scientific direction appeared in the early 70s of the last century, when the nucleotide sequences of small RNAs were first published and algorithms for predicting their secondary structure (the spatial arrangement of atoms in a molecule) were created.
A new era of bioinformatics has begun with the Human Genome Project, which aims to determine the sequence of nucleotides in human DNA and identify genes in the genome. The cost of DNA sequencing (nucleotide sequencing) has dropped by several orders of magnitude. This has led to a tremendous increase in the number of sequences in public databases. The graph below shows the growth in the number of sequences in the GenBank public database from December 1982 to February 2017 on a semi-log scale. In order for the accumulated data to become useful, they need to be analyzed in some way.

Growth in the number of sequences in GenBank from December 1982 to February 2017. Source: www.ncbi.nlm.nih.gov/genbank/statistics
One of the methods of sequence analysis in bioinformatics is sequence alignment. The essence of the method lies in the fact that the sequences of monomers of DNA, RNA or proteins are placed under each other in such a way as to see similar areas. The similarity of the primary structures (that is, the sequences) of two molecules may reflect their functional, structural, or evolutionary relationship. Since a sequence can be represented as a string with a specific alphabet (4 nucleotides for DNA and 20 amino acids for protein), alignment turns out to be a combinatorial task from CS (for example, line alignment is also used in natural language processing - NLP). However, the biology context adds some specificity to the problem.
Let's look at alignment using proteins as an example. One amino acid residue in the protein corresponds to one letter of the Latin alphabet in the sequence. The strings are written one below the other to achieve the best match. Matching elements are one below the other, "gaps" are replaced by "-" (gap). They designate indel , that is, the place of possible insertion (introduction into a molecule of one or more nucleotides or amino acids) and deletions ("dropout" of a nucleotide or amino acid).

An example of the alignment of the amino acid sequences of two proteins. Leucine (L) and isoleucine (I), which are isomers, are highlighted in blue - such a substitution in most cases does not affect the protein structure
However, how can you determine if the alignment is optimal? The first thing that comes to mind is to estimate the number of matches: the more matches, the better. However, in the context of biology, this is not entirely true. Substitutions (substitutions of one amino acid for another) are unequal: some substitutions (for example, S and T, D and E are residues that differ in structure by exactly one carbon atom) practically do not affect the structure of proteins. But replacing serine with tryptophan will greatly change the structure of the molecule. A quantitative criterion (weight or score) is entered to determine if the clearing is the best possible. To assess substitutions, so-called substitution matrices are used, based on the statistics of amino acid substitution in proteins with a known structure. The higher the number at the intersection of the matched letters, the higher the score.

New substitution matrices appear periodically. Here is the BLOSUM62 matrix.
The score also takes into account the presence of deletions. Usually, the penalty for “opening” a deletion is several orders of magnitude greater than for “continuing”. This is due to the fact that a section of several consecutive gaps is considered one mutation, and several gaps in different places are considered several. In the example below, the first pair of sequences is more similar than the second, because in the first case, the sequences are formally separated by one evolutionary event:

Now about the alignment algorithms themselves. There are two types of paired alignment (finding similar areas of two sequences): global and local. Global alignment implies that the sequences are homologous (similar) along their entire length. It includes both sequences in their entirety. However, with this approach, similar areas are not always well defined if there are few of them. Local alignment is used if the sequences are kept as homologous (for example, due to recombination) and unrelated sites. But it can not always get into the area of interest, moreover, there is a possibility of meeting an accidental similar area. To obtain a pairwise alignment, dynamic programming methods are used (solving a problem by dividing it into several identical subtasks connected recurrently). In programs for global alignment, the Needleman-Wunsch algorithm is often used , and for local alignment , the Smith-Waterman algorithm . You can read more about them by following the links.
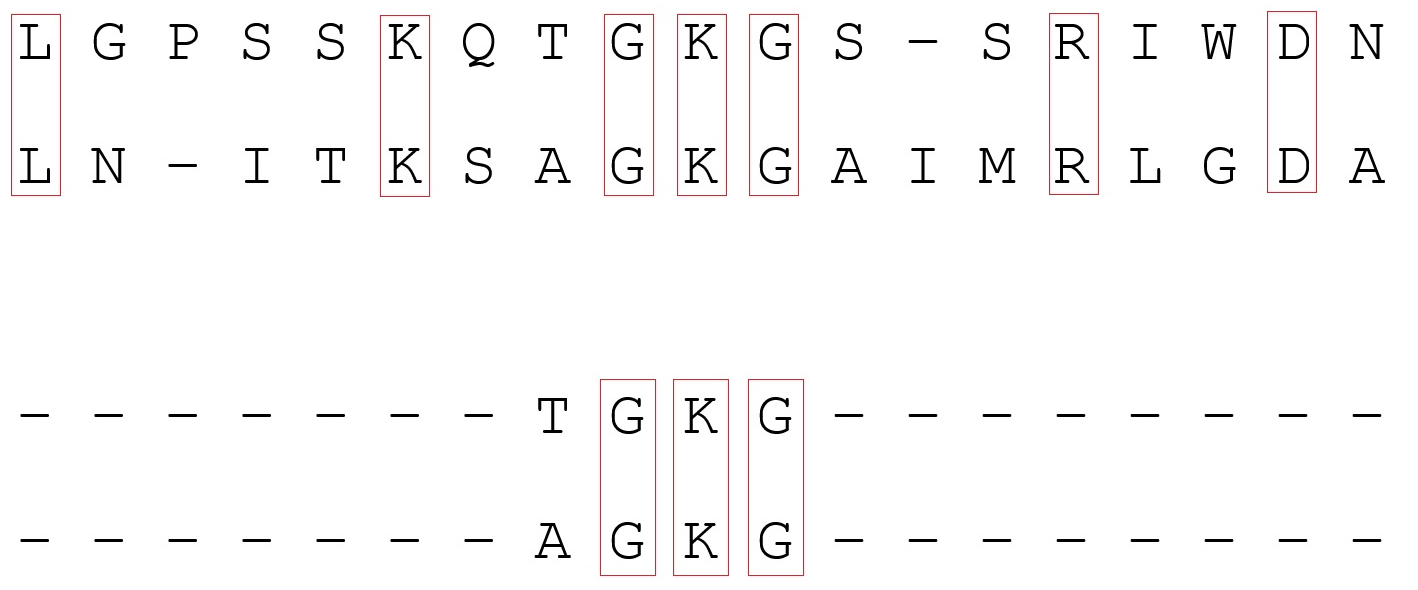
Alignment example: top is global, bottom is local. In the first case, alignment occurs along the entire length of the sequences; in the second, some homologous regions are found.
As you can see, the biological task can be completely reduced to the task from CS. Pairwise alignment using the mentioned algorithms requires about m * n additional memory (m, n are the lengths of the sequences), which modern home computers can easily handle. However, bioinformatics also has more non-trivial tasks, for example, multiple alignment (alignment of several sequences) for the reconstruction of phylogenetic trees... Even if we compare 10 very small proteins with a sequence length of about 100 characters, then an unacceptably large amount of additional memory will be required (the dimension of the array is 100 ^ 10). Therefore, in this case, the alignment is based on various heuristics.
Modeling the large-scale structure of the universe
Unlike biology, physics has gone side by side with Computer Science since the early days of computers. Before the creation of the first computers, the word "computer" (calculator) was called a special position - these were people who performed mathematical calculations on calculators. Thus, during the Manhattan Project, physicist Richard Feynman was the manager of a whole team of "calculators" who processed differential equations on adding machines.

"Computing room" of the Flight Research Center. Armstrong. USA, 1949
At the moment, CS methods are widely used in various fields of physics. For example, computational physics studies numerical algorithms for solving physical problems for which a quantitative theory has already been developed. In situations where direct observation of objects is difficult (this often happens in astronomy), computer modeling comes to the aid of scientists. Exactly such a case is the study of the large-scale structure of the Universe : observations of distant objects are difficult due to the absorption of electromagnetic radiation in the plane of the Milky Way, so modeling has become the main research method.

,
One of the tasks of modern cosmology is to explain the observed picture of the diversity of galaxies and their evolution. At the qualitative level, the physical processes occurring in galaxies are now known, therefore, the efforts of scientists are aimed at obtaining quantitative predictions. This will allow answering a number of fundamental questions, for example, about the properties of dark matter. But, before isolating the observed manifestations of dark matter, it is necessary to understand the behavior of ordinary matter. On a huge scale (several million light years), ordinary matter effectively behaves in the same way as dark: it is subject to one force of gravity, you can forget about the gas pressure. This makes it relatively easy to simulate the evolution of the large-scale structure of the Universe (Numerical methods,containing only dark or dust-like matter and well reproducing the large-scale structure of the distribution of galaxies, began to develop since the 1980s).
Dark matter is modeled as follows. The virtual cube, hundreds of millions of light years in size, is almost uniformly filled with test particles - bodies. From the very beginning, small inhomogeneities were present in the Universe, from which the entire observed structure arose, therefore, the filling is "almost uniform". Then the particles begin to “live their own lives” under the influence of gravity: the problem of N bodies is solved . The particles escaped from the cube are transferred to the opposite face, and the gravitational forces also propagate with the transfer. Thanks to this, the cube becomes, as it were, infinite, like the universe.

Approximate trajectories of three identical bodies located at the vertices of a non-isosceles triangle and having zero initial velocities
One of the most famous numerical models of this type is the Millenium , which has a cube size of more than 1.5 billion light years and about 10 billion particles. In the following years, several larger models were made: the Horizon Run with a cube side 4 times larger than the Millenium, and the Dark Sky with 16 times the Millenium. These and similar models have played a key role in projects to validate the now generally accepted Lambda-CDM model. (A universe containing about 70% dark energy, 25% dark matter and 5% ordinary matter).

Millenium: , ; — . .
Downscaling causes problems in matching observations and numerical models with one dark matter. On a smaller scale (the scale of propagation of shock waves from supernovae), matter can no longer be considered dusty. It is necessary to take into account hydrodynamics, cooling and heating of gas by radiation, and much more. To take into account all the laws of physics in modeling, some simplifications are made: for example, you can break the model cube into a lattice of cells (sublattice physics), and assume that when a certain density and temperature in the cell is reached, part of the gas will instantly turn into a star. This class of models includes the EAGLE and illustris projects . One of the results of these projects is the reproduction of the Tully-Fisher relation between the luminosity of the galaxy and the speed of rotation of the disk.
Linguistics and machine learning: one step closer to solving a 4,000-year-old mystery
CS methods find applications in more unexpected areas, for example, in the study of ancient languages and writing systems. Thus, a study by a group of scientists led by Rajesh P.N. Rao, a professor at the University of Washington, shed light on the mystery of the Indus Valley writing.
The Indus script, used between 2600-1900 BC in what is now East Pakistan and northwestern India, belonged to a civilization no less complex and mysterious than its Mesopotamian and Egyptian contemporaries. There are very few written sources left from it: archaeologists have found only about 1,500 unique inscriptions on fragments of ceramics, tablets and seals. The longest lettering is only 27 characters long.

Inscriptions on seals from the Indus Valley
In the scientific community, there were various hypotheses about the "mysterious symbols". Some experts considered symbols to be nothing more than just "pretty pictures." So in 2004, linguist Steve Farmer published an article in which it was argued that the Indus writing is nothing more than political and religious symbols. His version, although controversial, still found its supporters.
Rajesha P.N. Rao, a machine learning scientist, read about Indus writing in high school. A group of scientists under his leadership decided to conduct a statistical analysis of existing reliable documents. In the course of research using Markov chains(one of the first disciplines in which Markov chains found practical application was textual criticism) the conditional entropy was compared symbols from the Indus script with the entropy of linguistic and non-linguistic sign sequences. Conditional entropy is the entropy for an alphabet for which the probabilities of one letter after another are known. Several systems were selected for comparison. The linguistic systems included: Sumerian logographic writing, Old Tamil Abugida, Sanskrit of the Rig Veda, modern English (words and letters were studied separately) and the Fortran programming language. Non-linguistic systems were divided into two groups. The first included systems with a rigid order of signs (artificial set of signs No. 1), the second - systems with a flexible order (proteins of bacteria, human DNA, artificial set of signs No. 2). As a result, it turned out that the proto-Indian writing turned out to be moderately ordered, like the writing of the spoken languages:the entropy of existing documents is similar to the entropy of the Sumerian and Tamil scripts.

Conditional entropy for various linguistic and non-linguistic systems
This result refuted the hypothesis about the ornamental use of signs. And although CS methods helped to confirm the version that the symbols from the Indus Valley are most likely a writing system, the case has not yet come to decryption.
Conclusion
Of course, many areas where CS methods find application are left overboard. It is simply impossible in one article to reveal how modern science relies on computer technology. However, I hope the given examples show how different problems can be solved, including by CS methods.
Cloud servers from Macleod are fast and secure.
Register using the link above or by clicking on the banner and get a 10% discount for the first month of renting a server of any configuration!
