
Based on a talk at Numerous Numerosity: an interdisciplinary meeting focusing on the concepts of power, ordinality, and arithmetic in various sciences .
Everyone should have numbers ... right?
The aliens arrive by spaceship . Of course, one might think that in order to possess all these technologies, they must have an understanding of numbers. Or maybe an isolated tribe can be found deep in the jungle. Surely they should also have an idea of numbers. To us, numbers seem so natural - and "obvious" that it's hard to imagine that someone might not have them. But if you dig a little deeper, it's not so obvious.
It is said that there are human languages that have words for "one," "pair," and "many," but no words for specific large numbers. In our modern technological world, this seems inconceivable. But imagine that you are in the jungle with your dogs. Each dog has certain characteristics and most likely a specific name. Why think of them together as all countable “just dogs” at all?
Imagine you have sophisticated artificial intelligence. Maybe it's part of a starship. And the following calculation takes place in it :

Where are the numbers here? What is there to count?
Let's change the calculation rule a bit. Here's what we get:

And now we have something where the numbers seem to be more appropriate. We can distinguish several structures. They are not all the same, but they do have certain characteristics in common. And we can imagine that we are describing what we see, simply saying, for example, "There are 11 objects ...".
What underlies the idea of numbers?
Dogs. Sheeps. Trees. Stars. It doesn't matter what these things are. If you have a collection that you think consists of the same things, you can imagine how to count them. Just look at each of them in turn, at each step applying a particular operation to the last result of your count, so that computationally, you build something like this:
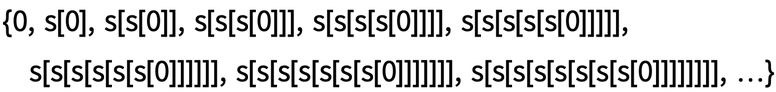
For our ordinary integers, we can interpret s as a "successor function" or "add 1". But at a fundamental level, all that really matters is that we have reduced looking at each of our original things in isolation to simply reusing one operation over and over that produces a chain of results.
However, in order to get to this point, an important step must be taken early on: we must have some kind of definite concept of "things" - or, in fact, the concept of separate objects. Our everyday world is, of course, full of them. There are different people. Certain giraffes. Certain chairs. But this becomes much less clear if we think about clouds, for example. Or gusts of wind. Or abstract ideas.
So what allows us to identify a certain "countable thing"? Somehow a "thing" must have a certain existence - some degree of permanence or universality and some ability to be independent and separate from other things.
We can imagine many different criteria. But there is one general approach that we humans are very familiar with: the way we talk about "things" in human language. Let's take some visual scene. But when we describe it in human language, we, in fact, always come up with a symbolic description of the scene .
There is a cluster of orange pixels. There are brown ones over there. But in human language we are trying to reduce all these details to a much simpler symbolic description. There is a chair over there. The table is over there.
It is not obvious that we will be able to carry out such "symbolization" in any meaningful way. But what makes this possible is that the parts of what we see are reproducible enough that we can consider them “the same things” and, for example, give them certain names in human language. "This is a table, this is a chair, etc."
There is a complex feedback loop that I have written about elsewhere . If we see something often enough, it makes sense to give it a name ("this is a bush"; "this is a typeface"). But once we give the thing a name, it will be much easier for us to talk and think about it. And so we tend to find or create more of what will be more common in our environment and more familiar to us.
In the abstract, it is not obvious that "symbolization" is possible. It may happen that the fundamental behavior of the world will always generate more and more variety and complexity, and will never produce any "repeating objects" that, for example, could reasonably be given consistent names.
One can imagine that once one believes that the world follows certain laws, there will inevitably be sufficient regularity to warrant the possibility of "symbolization." But this ignores the phenomenon of computational irreducibility .
Consider the rule:

One can imagine that with the help of such a simple rule, we will inevitably be able to describe the action that it produces in a simple way. And yes, we can always use a rule to understand what action it triggers. But the fundamental fact of the computational universe is that the result does not have to be simple:

And in general, we can expect an action to be computationally indecomposable, in the sense that it is impossible to replicate it without effectively tracking every step in the application of the rule.
With such an action, it

is quite possible to present a complete symbolic description of what is happening. But as soon as computational irreducibility appears, this will become impossible. There will be no way to get "Succinct" symbolic description of the entire action.
So why do we manage to describe so much in language in a "symbolic" way? It turns out that even when a system - such as our universe - is fundamentally computationally irreducible, it is inevitable that it will have pockets of computational reducibility. And these pockets of computational reducibility are critical to how we operate in the universe. Because they allow us to have a holistic perception of the world, when everything happens predictably in accordance with certain laws, and so on.
And these pockets also mean that - even if we cannot describe things symbolically - there is always something that we can describe. And we can expect the concept of numbers to be useful.
To be continued...
Ontol
The Ontol project is a Github for knowledge / wisdom (modeled on DIKW ). Ontol is designed to 100 times reduce friction and the time of access to information that forms an adequate worldview.

Each user can create / copy Ontol (list of top 10/100 articles / videos) on an important topic for him and update / modify it throughout his life. For example, this translation of Wolfram is in my Ontol on the topic #math in the top 10 .
Ontol - Solves the problem of information overload and (marketing) misinformation. With the help of thousands of volunteers / hackers / intellectuals (who will put their skins on the line), we can filter out all the available wisdom and knowledge of humankind and benefit billions of people on the horizon of 100+ years.
While I saw the prototype of the backend, I share my best finds in my entire life (from the series: "oh, sorry I didn't know this before!") In the telegram channel: t.me/ontol