Clever Geek Handbook

Diving into statistics with Python. Part 2. Student's distribution

Good day, habraledi and habragentelmen! In this article, we'll continue our dive into statistics with Python. If anyone missed the start of the dive, here's a link to the first part . Well, if not, I still recommend keeping Sarah Boslaf's open book, Statistics for All, close at hand. I also recommend running notepad to experiment with code and graphs.





As Andrew Lang said, “ Statistics are to a politician like a street lamp to a drunken bummer: a prop rather than a lighting. ” The same can be said for this article for newbies. It is unlikely that you will learn a lot of new knowledge here, but I hope this article will help you understand how to use Python to facilitate self-study of statistics.





Why invent new allocations?

Imagine ... so, before we imagine anything, let's do all the necessary imports again:





import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from pylab import rcParams
sns.set()
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'svg'
np.random.seed(42)

, , . , , - , . 1000 100- , . : 





gen_pop = np.trunc(stats.norm.rvs(loc=80, scale=5, size=1000))
gen_pop[gen_pop>100]=100
print(f'mean = {gen_pop.mean():.3}')
print(f'std = {gen_pop.std():.3}')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
mean = 79.5
std = 4.95

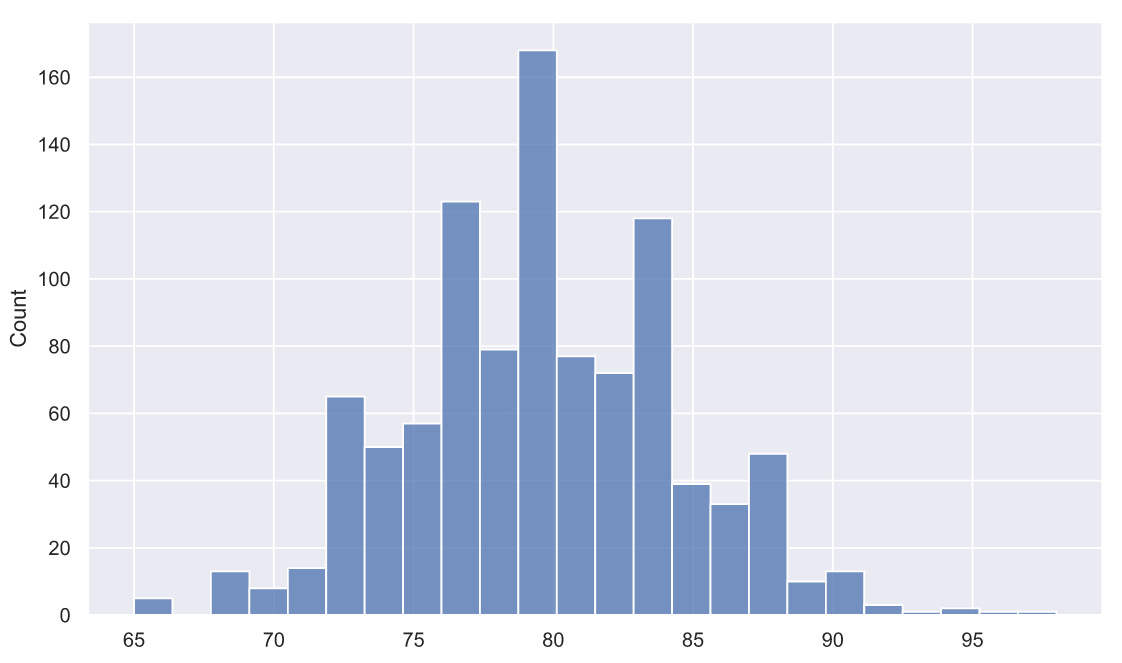
, , . 80 5 . , , , , , - .





, . , - . , - , ? - . , 10 , :





[89, 99, 93, 84, 79, 61, 82, 81, 87, 82]

Z- :





Z = \ frac {\ bar {x} - \ mu} {\ frac {\ sigma} {\ sqrt {n}}}

\ bar {x}- , \ mu \ sigma , n- . :





sample = np.array([89,99,93,84,79,61,82,81,87,82])
sample.mean()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
83.7

Z-:





z = 10**0.5*(sample.mean()-80)/5
z
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
2.340085468524603

p-value: 





1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
0.019279327322753836

, , : Z- 0 2 , .. 10 , , , 0.02. , 10 , "" N (80, 5 ^ {2}), , 10 "" 83.7 2%. , , , , . .





- 10 , , :





sample.std(ddof=1)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
10.055954565441423
ddof std

\ sigma, , s, . :





\ begin {align *} & \ sigma = {\ sqrt {{\ frac {1} {n}} \ sum _ {i = 1} ^ {n} \ left (x_ {i} - {\ mu} \ right ) ^ {2}}} \\ & \\ & s = {\ sqrt {{\ frac {1} {n - 1}} \ sum _ {i = 1} ^ {n} \ left (x_ {i} - {\ bar {x}} \ right) ^ {2}}} \ end {align *}

, , \ sigma . - \ mu n, s n - 1. n - 1 n? , \ mu \ bar {x} - s , \ sigma . n - 1 , - .





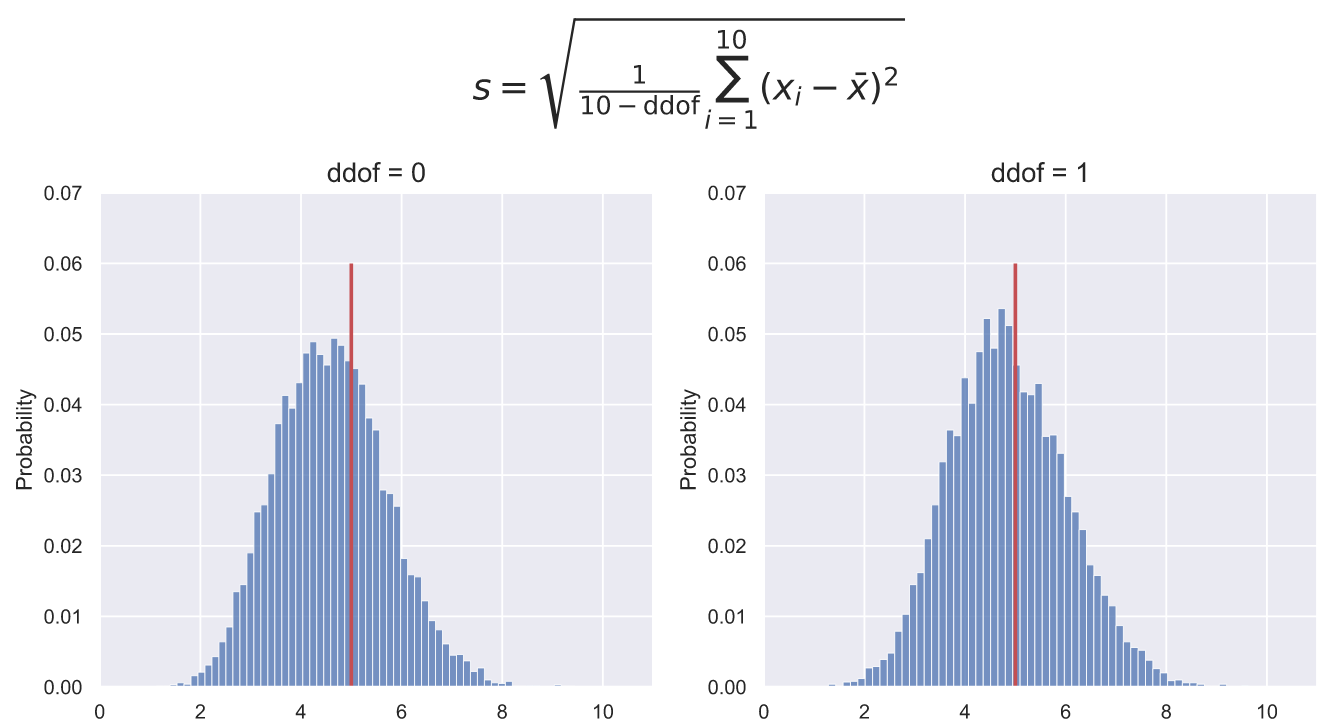
, std() NumPy ddof, 0, std() , , ddof=1. . , 10000 10 N (80, 5 ^ {2}) , , ddof=0 . ddof=1 , - , ddof=0:





fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (12, 5))

for i in [0, 1]:
    deviations = np.std(stats.norm.rvs(80, 5, (10000, 10)), axis=1, ddof=i)
    sns.histplot(x=deviations ,stat='probability', ax=ax[i])
    ax[i].vlines(5, 0, 0.06, color='r', lw=2)
    ax[i].set_title('ddof = ' + str(i), fontsize = 15)
    ax[i].set_ylim(0, 0.07)
    ax[i].set_xlim(0, 11)
fig.suptitle(r'$s={\sqrt {{\frac {1}{10 - \mathrm{ddof}}}\sum _{i=1}^{10}\left(x_{i}-{\bar {x}}\right)^{2}}}$',
             fontsize = 20, y=1.15);

, Z-? , - , . 5000 10 , N (80, 5) :





deviations  = np.std(stats.norm.rvs(80, 5, (5000, 10)), axis=1, ddof=1)
sns.histplot(x=deviations ,stat='probability');

, , 10- . . , , 10 2%, , ( ) 10 0. , , : 10- , .





, , , : - , - , . , "" N (80, 10 ^ {2}), Z- p-value 10- :





z = 10**0.5*(sample.mean()-80)/10
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'z = {z:.3}')
print(f'p-value = {p:.4}')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
z = 1.17
p-value = 0.242

, N (80, 5 ^ {2}) , , , .. , N (80, 10 ^ {2}), . 2%, 25%. , - \ sigma s.





, ? ! , : (, , - )





Z = \ frac {\ bar {x} - \ mu} {\ frac {\ sigma} {\ sqrt {n}}} \; ; \; \; \; T = \ frac {\ bar {x} - \ mu} {\ frac {s} {\ sqrt {n}}}.

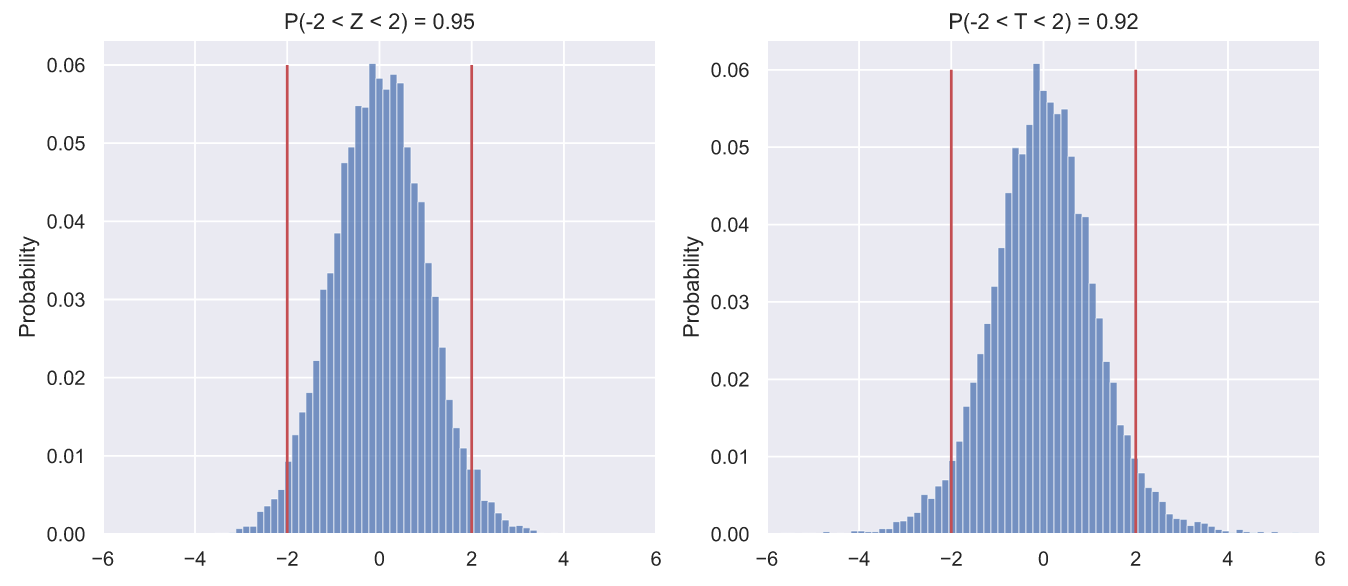
T-, Z- , \ sigma , s. 10000 N (80, {5} ^ 2), Z- T-, :





fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (12, 5))

N = 10000
samples = stats.norm.rvs(80, 5, (N, 10))
statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
              lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]
title = 'ZT'
bins = np.linspace(-6, 6, 80, endpoint=True)

for i in range(2):
    values = statistics[i](samples)
    sns.histplot(x=values ,stat='probability', bins=bins, ax=ax[i])
    p = values[(values > -2)&(values < 2)].size/N
    ax[i].set_title('P(-2 < {} < 2) = {:.3}'.format(title[i], p))
    ax[i].set_xlim(-6, 6)
    ax[i].vlines([-2, 2], 0, 0.06, color='r');

- :





import matplotlib.animation as animation

fig, axes = plt.subplots(nrows=1, ncols=2, figsize = (18, 8))

def animate(i):
    for ax in axes:
        ax.clear()
    N = 10000
    samples = stats.norm.rvs(80, 5, (N, 10))
    statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
                  lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]
    title = 'ZT'
    bins = np.linspace(-6, 6, 80, endpoint=True)

    for j in range(2):
        values = statistics[j](samples)
        sns.histplot(x=values ,stat='probability', bins=bins, ax=axes[j])
        p = values[(values > -2)&(values < 2)].size/N
        axes[j].set_title(r'$P(-2\sigma < {} < 2\sigma) = {:.3}$'.format(title[j], p))
        axes[j].set_xlim(-6, 6)
        axes[j].set_ylim(0, 0.07)
        axes[j].vlines([-2, 2], 0, 0.06, color='r')
    return axes

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(7),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('statistics_dist.gif',
                 writer='imagemagick', 
                 fps=1)

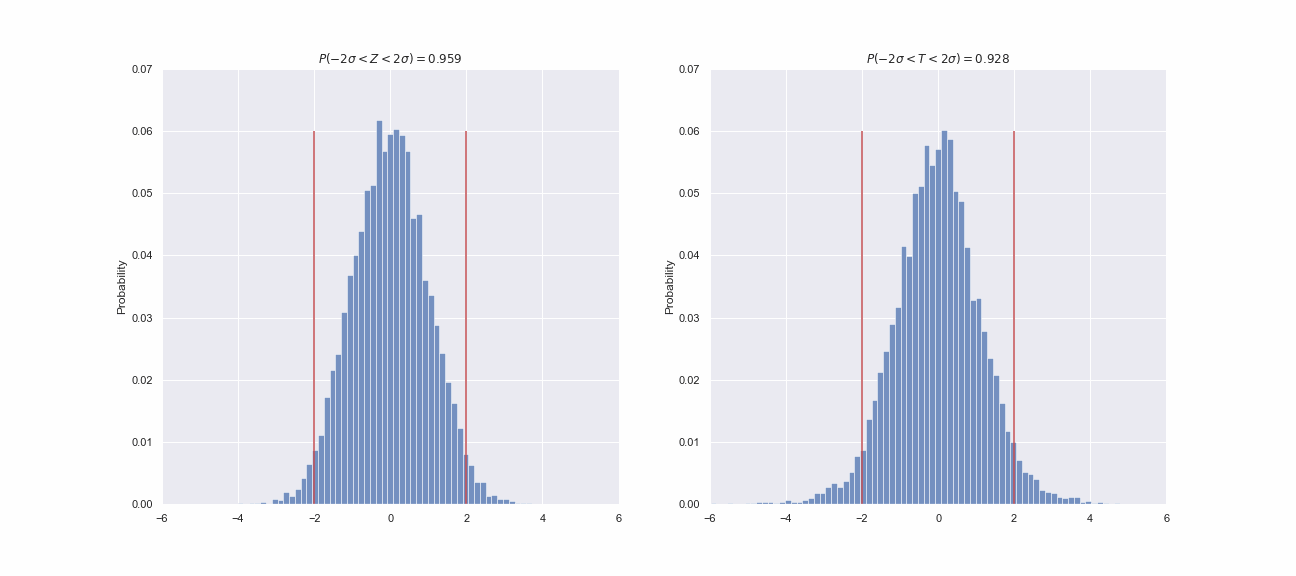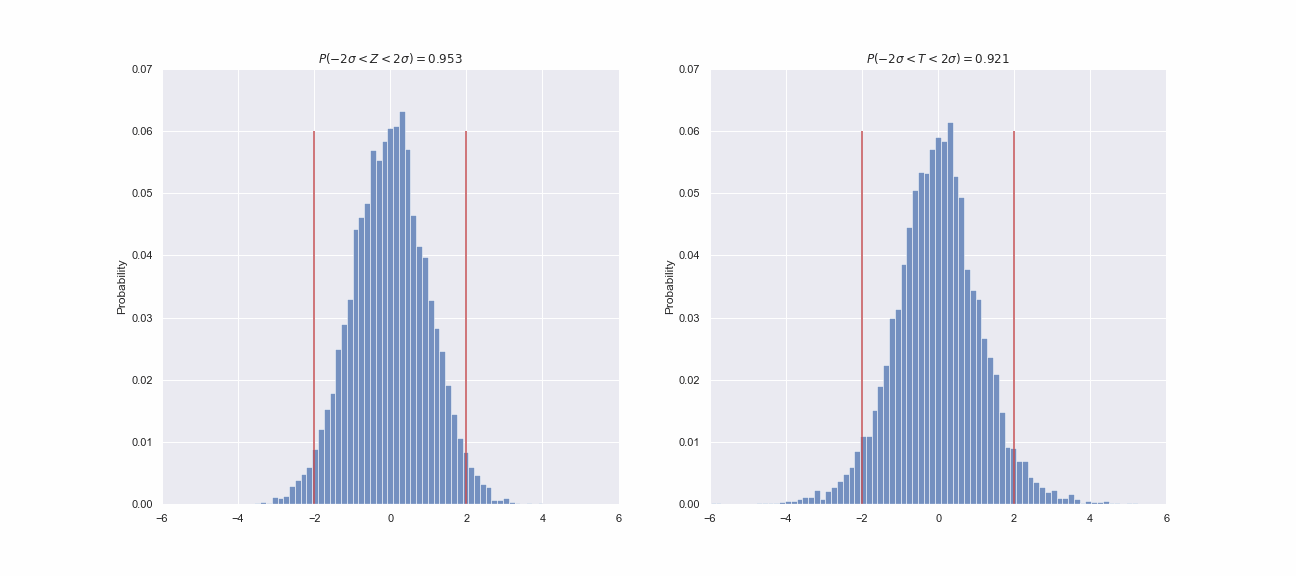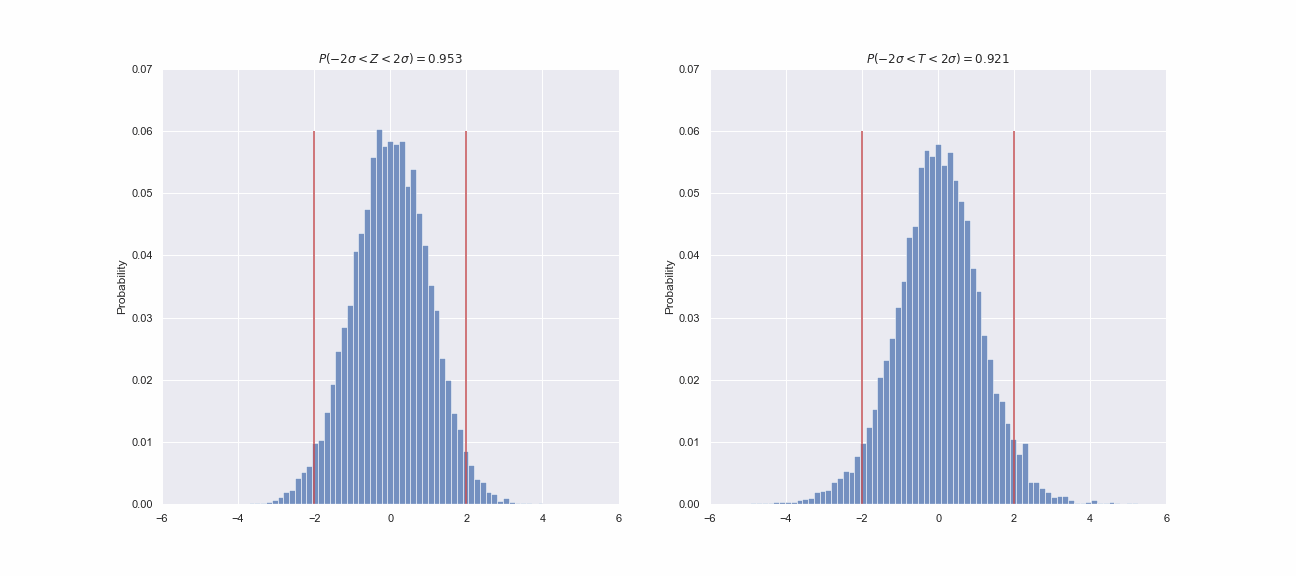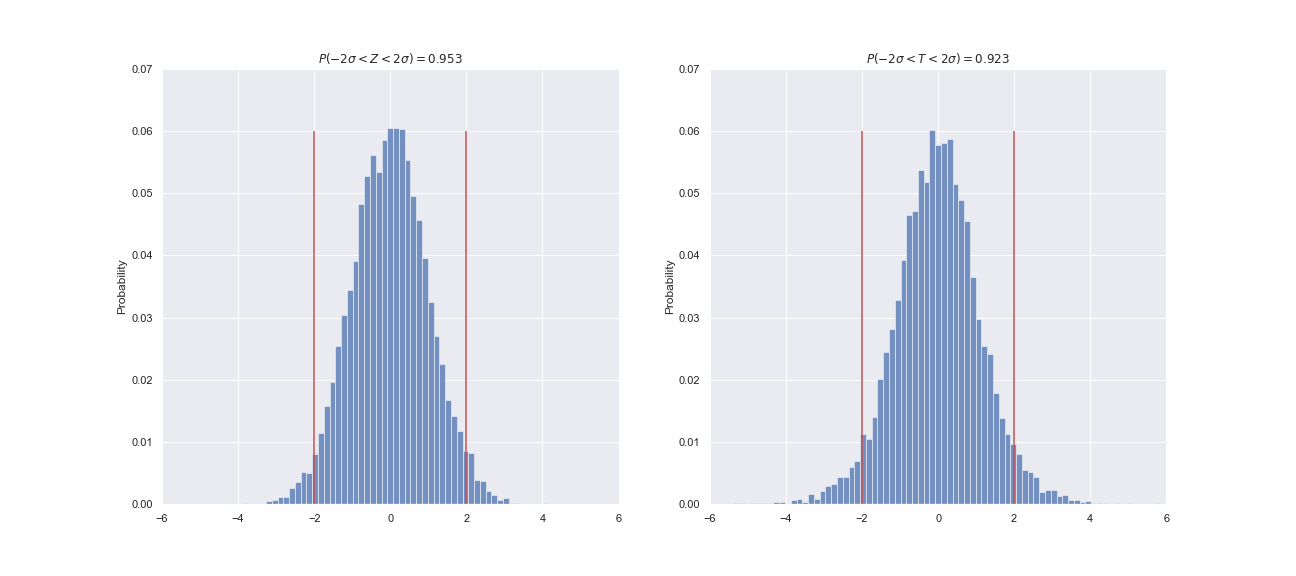
, , . ? -, , . , , ? , , N (0, 1) [-2 \ sigma; 2 \ sigma] 95.5% . Z- , T- , 92-93% . , , - , :





statistics = [lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/5,
              lambda x: 10**0.5*(np.mean(x, axis=1) - 80)/np.std(x, axis=1, ddof=1)]

quantity = 50
N=10000
result = []
for i in range(quantity):
    samples = stats.norm.rvs(80, 5, (N, 10))
    Z = statistics[0](samples)
    p_z = Z[(Z > -2)&((Z < 2))].size/N
    T = statistics[1](samples)
    p_t = T[(T > -2)&((T < 2))].size/N
    result.append([p_z, p_t])

result = np.array(result)
fig, ax = plt.subplots()

line1, line2 = ax.plot(np.arange(quantity), result)
ax.legend([line1, line2], 
          [r'$P(-2\sigma < {} < 2\sigma)$'.format(i) for i in 'ZT'])
ax.hlines(result.mean(axis=0), 0, 50, color='0.6');

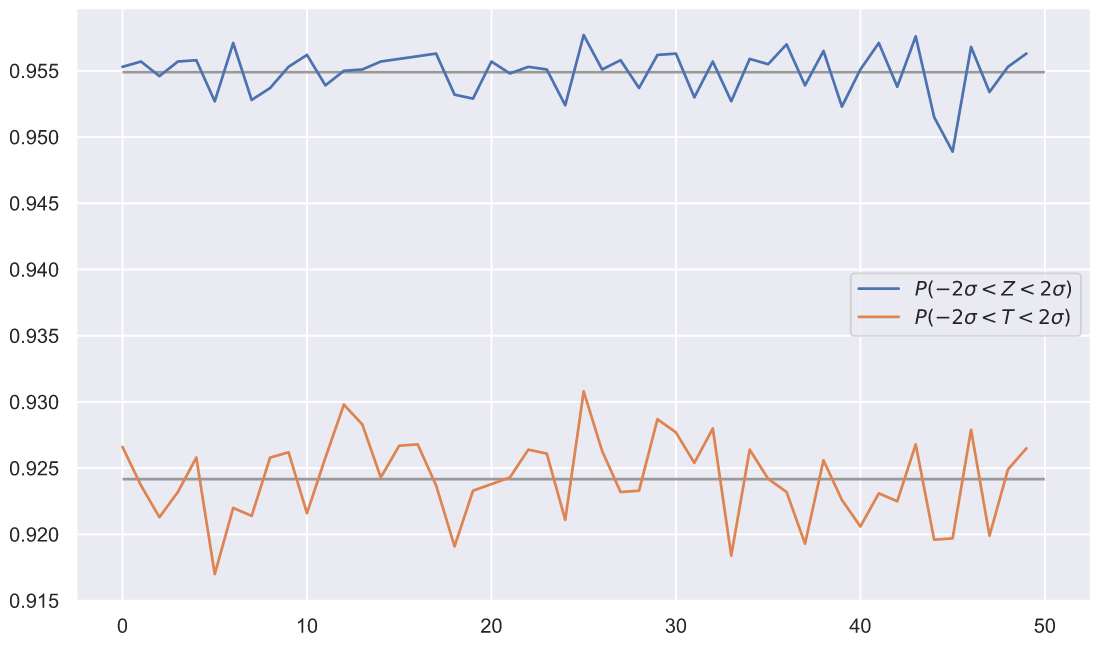
50 . , , , , . ? , ! Z- T- , . , T- ? , - . , , - , , , . , . , - , , \ sigma s.





Z-, \ bar {x} , s - . 10000 N (80, 5) 10 , :





#     ,
#    svg  png:
#%config InlineBackend.figure_format = 'png'

N = 10000
samples = stats.norm.rvs(80, 5, (N, 10))

means = samples.mean(axis=1)
deviations = samples.std(ddof=1, axis=1)
T = statistics[1](samples)
P = (T > -2)&((T < 2))

fig, ax = plt.subplots()

ax.scatter(means[P], deviations[P], c='b', alpha=0.7,
           label=r'$\left | T \right | < 2\sigma$')
ax.scatter(means[~P], deviations[~P], c='r', alpha=0.7,
           label=r'$\left | T \right | > 2\sigma$')

mean_x = np.linspace(75, 85, 300)
s = np.abs(10**0.5*(mean_x - 80)/2)
ax.plot(mean_x, s, color='k',
        label=r'$\frac{\sqrt{n}(\bar{x}-\mu)}{2}$')
ax.legend(loc = 'upper right', fontsize = 15)
ax.set_title('   \n  ',
             fontsize=15)
ax.set_xlabel(r'   ($\bar{x}$)',
              fontsize=15)
ax.set_ylabel(r'   ($s$)',
              fontsize=15);

, . , , \ bar {x} s , .. . , , N (\ mu, \ sigma ^ {2}), \ left | \ bar {x} - \ mu \ right | \ left | s - \ sigma \ right |. , ( ) , :





\ left | \ bar {x} - \ mu \ right | > \ frac {2 \ sigma s} {\ sqrt {n}}

, \ sigma = 1, .. , , , \ mu = 80, n = 10 :





\left | \bar{x} - 80 \right | >\frac{2s}{\sqrt{10}}

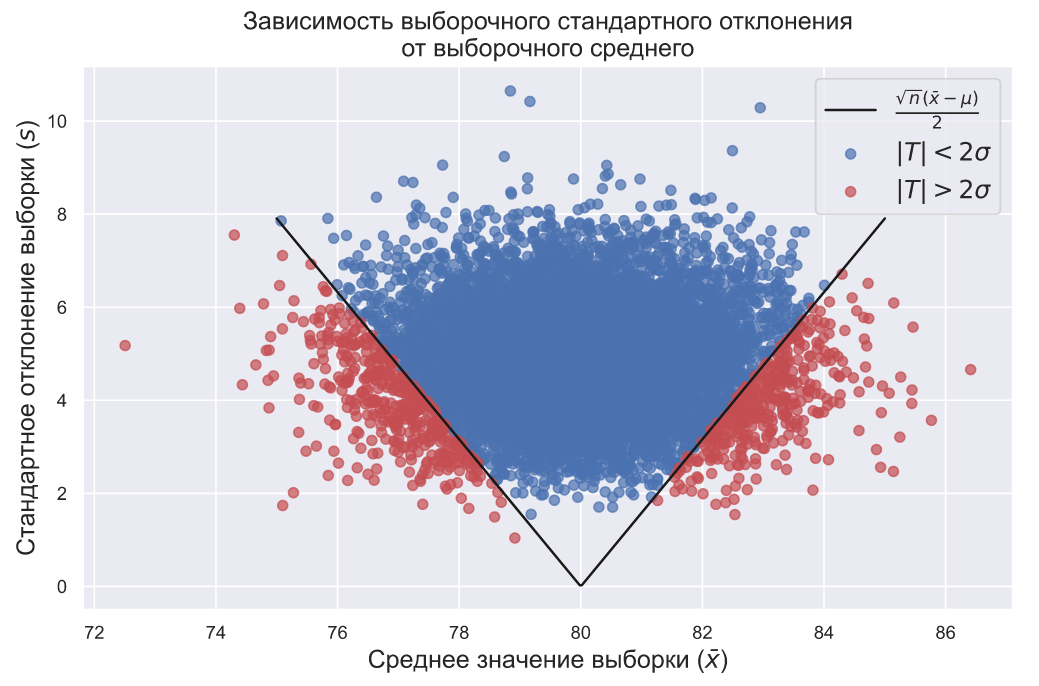
, [-2\sigma; 2\sigma], , 92,5% .





? , . , ( ) 100- . , , ( ). 10- 82- , 2- . , , . \mu=80, , .. \sigma = s = 2? Z-:





Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} = \frac{82 - 80}{\frac{2}{\sqrt{10}}} \approx 3.16

N(80, 2^{2}) p-value:





z = 10**0.5*(82-80)/2
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'p-value = {p:.2}')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
p-value = 0.0016

10 82- 2%. N(80, 2^{2}). , \sigma = s = 2, , , .





, , , . ( \left | \bar{x} - \mu \right |) ( s).





10 . 82 , , , 9- . ? :





z = 10**0.5*(82-80)/9
p = 1 - (stats.norm.cdf(z) - stats.norm.cdf(-z))
print(f'p-value = {p:.2}')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
p-value = 0.48

10 \bar{x} = 82 s = 9 N(80, 9^{2}) . , , - .





, , . :





import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 10000
    
    samples = stats.norm.rvs(80, 5, (N, i))

    means = samples.mean(axis=1)
    deviations = samples.std(ddof=1, axis=1)
    T = i**0.5*(np.mean(samples, axis=1) - 80)/np.std(samples, axis=1, ddof=1)
    P = (T > -2)&((T < 2))
    
    prob = T[P].size/N
    ax.set_title(r' $s$  $\bar{x}$  $n = $' + r'${}$'.format(i),
                 fontsize = 20)
    ax.scatter(means[P], deviations[P], c='b', alpha=0.7,
               label=r'$\left | T \right | < 2\sigma$')
    ax.scatter(means[~P], deviations[~P], c='r', alpha=0.7,
               label=r'$\left | T \right | > 2\sigma$')

    mean_x = np.linspace(75, 85, 300)
    s = np.abs(i**0.5*(mean_x - 80)/2)
    ax.plot(mean_x, s, color='k',
            label=r'$\frac{\sqrt{n}(\bar{x}-\mu)}{2}$')
    ax.legend(loc = 'upper right', fontsize = 15)
    ax.set_xlim(70, 90)
    ax.set_ylim(0, 10)
    ax.set_xlabel(r'   ($\bar{x}$)',
              fontsize='20')
    ax.set_ylabel(r'   ($s$)',
              fontsize='20')
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(5, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('sigma_rel.gif',
                 writer='imagemagick', 
                 fps=3)

, \bar{x} s \mu \sigma N(\mu, \sigma^{2}), . n Z-, n .





! , ? - , , . , , 10- :





[89,99,93,84,79,61,82,81,87,82]

\bar{x} = 83.7, s = 10.06, , , , , N(80, 5^{2}). Z-, T-, Z- , \sigma s. , - N(80, 5^{2}), N(80, 10.06^{2})- ? s?: , N(80, 1^{2}), N(80, 5^{2}), N(80, 7^{2}) \sigma?





, . , - . , N(80, 5^{2}), , , 10 , 10 . , N(80, 5^{2}) . , - , .





: \bar{x} = 83.7, s = 10.06, N(80, \sigma^{2}) \sigma. , , 83<\bar{x}<84 9.5<s<10.5:





N = 10000
sigma = np.linspace(5, 20, 151)
prob = []

for i in sigma:
    p = []
    for j in range(10):
        samples = stats.norm.rvs(80, i, (N, 10))
        means = samples.mean(axis=1)
        deviations = samples.std(ddof=1, axis=1)
        p_m = means[(means >= 83) & (means <= 84)].size/N
        p_d = deviations[(deviations >= 9.5) & (deviations <= 10.5)].size/N
        p.append(p_m*p_d)
    prob.append(sum(p)/len(p))
prob = np.array(prob)

fig, ax = plt.subplots()
ax.plot(sigma, prob)
ax.set_xlabel(r'    ($\sigma$)',
              fontsize=20)
ax.set_ylabel('',
              fontsize=20);

, \sigma \approx 10. , , \sigma, s. - , , , , . .





T-?

, - - . 1% , - . , , . , - -. ?





- ! , - , "" t-. , , , . , , 1943 , 50% . , - .





, "" . , ( !) , "" , :





t = \frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}

t-, . , , "", , , , , - . " ", "t-" , .





:





t={\frac {Y_{0}}{{\sqrt {{\frac {1}{n}}\sum \limits _{{i=1}}^{n}Y_{i}^{2}}}}},

" " . Y_{i} , .. {\displaystyle Y_{i}\sim {\mathcal {N}}(0,1),;i=0,\ldots ,n}, n, .. , . - , :





t\sim {\mathrm {t}}(n)

, :





import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 15000
    
    x = np.linspace(-5, 5, 100)
    ax.plot(x, stats.norm.pdf(x, 0, 1), color='r')
    
    samples = stats.norm.rvs(0, 1, (N, i))
    
    t = samples[:, 0]/np.sqrt(np.mean(samples[:, 1:]**2, axis=1))
    t = t[(t>-5)&(t<5)]
    sns.histplot(x=t, bins=np.linspace(-5, 5, 100), stat='density', ax=ax)
    
    ax.set_title(r'  $t(n)$  n = ' + str(i), fontsize = 20)
    ax.set_xlim(-5, 5)
    ax.set_ylim(0, 0.5)
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(2, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('t_rel_of_df.gif',
                 writer='imagemagick', 
                 fps=3)

, n, , , N(0, 1). , , :





{\ displaystyle f_ {t} (y) = {\ frac {\ Gamma \ left ({\ frac {n + 1} {2}} \ right)} {{\ sqrt {n \ pi}} \, \ Gamma \ left ({\ frac {n} {2}} \ right)}} \, \ left (1 + {\ frac {y ^ {2}} {n}} \ right) ^ {- {\ frac {n +1} {2}}}}

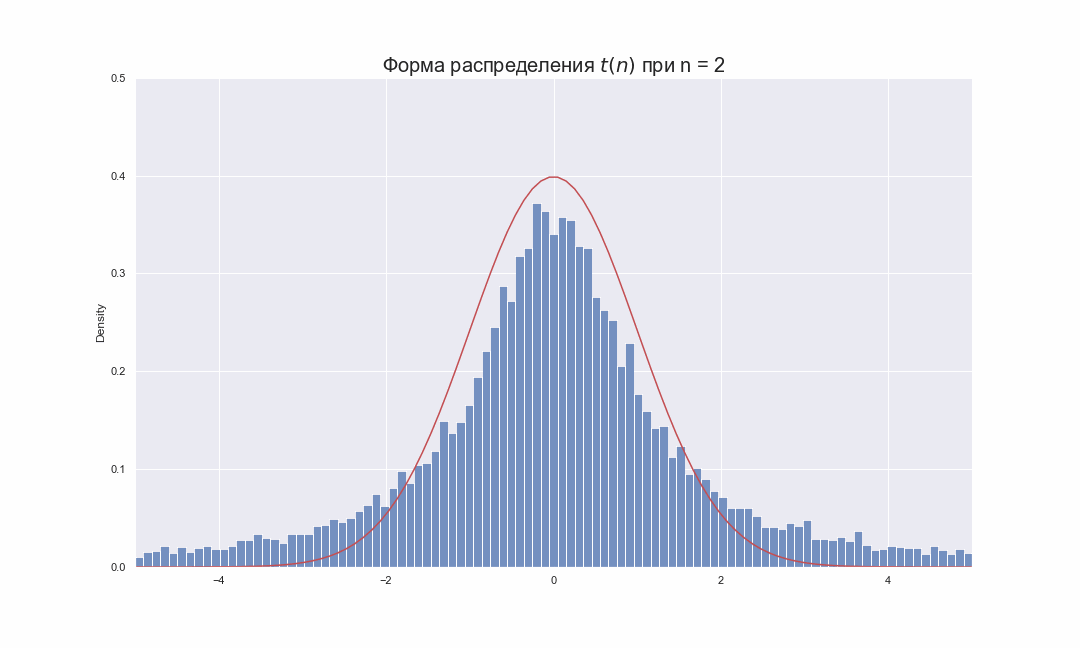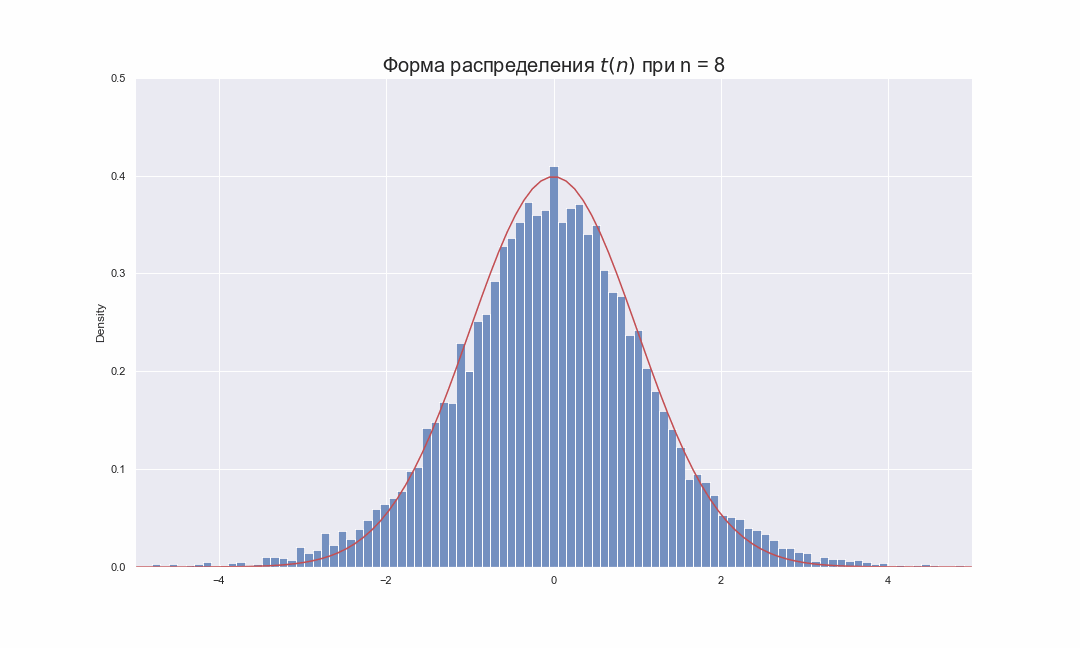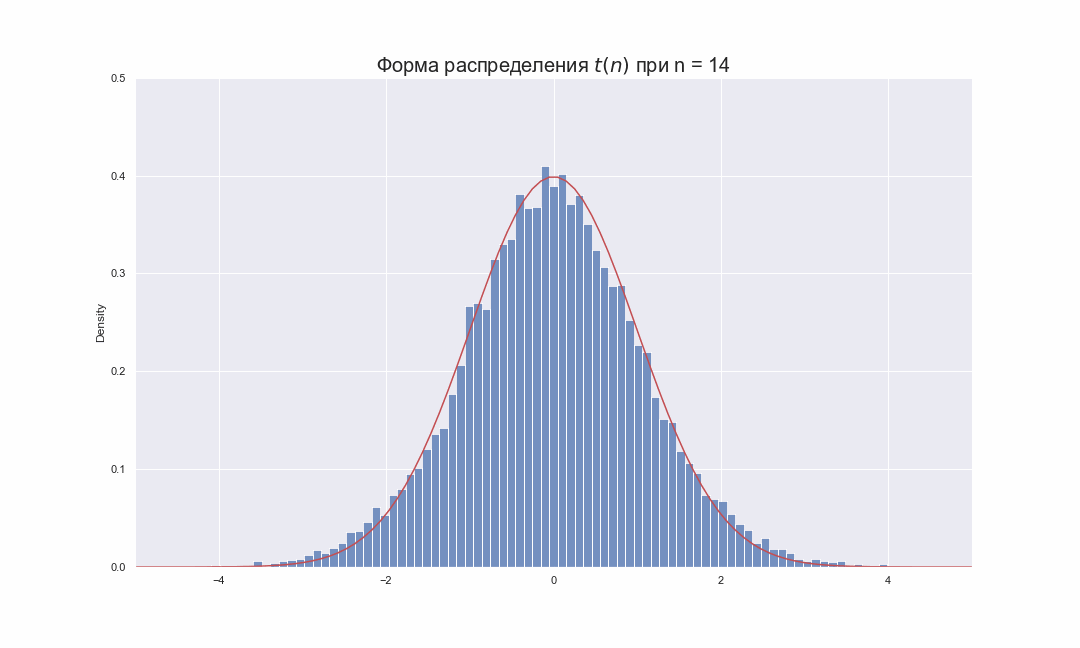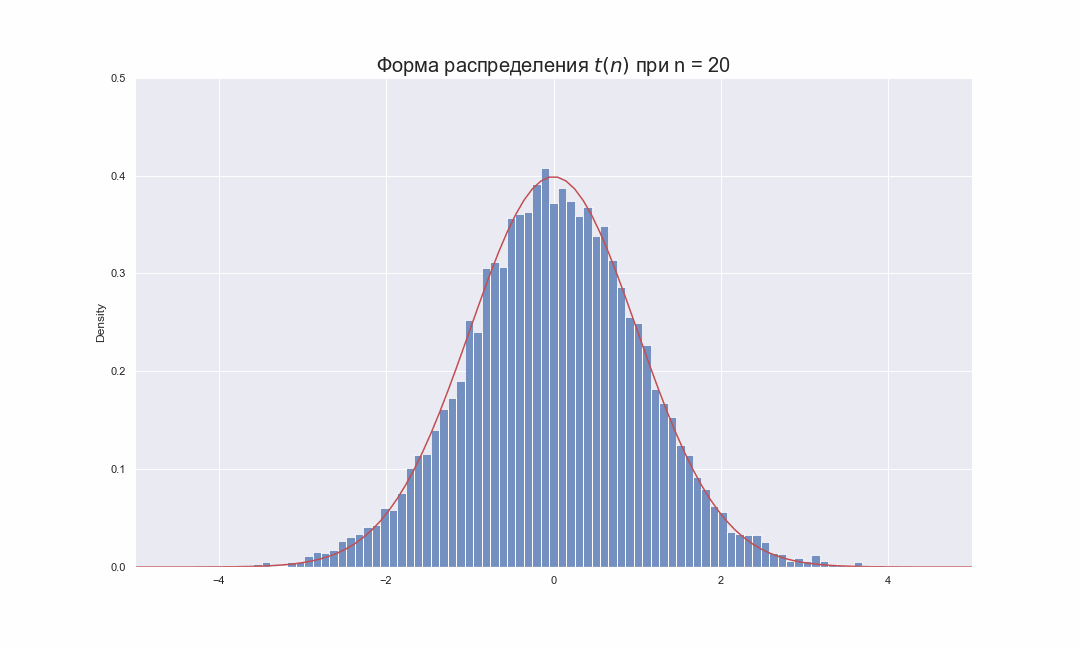
SciPy:





import matplotlib.animation as animation

fig, ax = plt.subplots(figsize = (15, 9))

def animate(i):
    ax.clear()
    N = 15000
    
    x = np.linspace(-5, 5, 100)
    ax.plot(x, stats.norm.pdf(x, 0, 1), color='r')
    ax.plot(x, stats.t.pdf(x, df=i))
    
    ax.set_title(r'  $t(n)$  n = ' + str(i), fontsize = 20)
    ax.set_xlim(-5, 5)
    ax.set_ylim(0, 0.45)
    return ax

dist_animation = animation.FuncAnimation(fig, 
                                      animate, 
                                      frames=np.arange(2, 21),
                                      interval = 200,
                                      repeat = False)

dist_animation.save('t_pdf_rel_of_df.gif',
                 writer='imagemagick', 
                 fps=3)

, n( df ) . - , , n, .





t-

t- SciPy :





sample = np.array([89,99,93,84,79,61,82,81,87,82])

stats.ttest_1samp(sample, 80)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
Ttest_1sampResult(statistic=1.163532240174695, pvalue=0.2745321678073461)

:





T = 9**0.5*(sample.mean() -80)/sample.std()
T
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
1.163532240174695

, n = 10, df, n - 1. , 1 , , , . :





T = 10**0.5*(sample.mean() -80)/sample.std(ddof=1)
T
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
1.1635322401746953

, t- , p-value? , - , p-value Z-, t-:





t = stats.t(df=9)
fig, ax = plt.subplots()
x = np.linspace(t.ppf(0.001), t.ppf(0.999), 300)
ax.plot(x, t.pdf(x))
ax.hlines(0, x.min(), x.max(), lw=1, color='k')
ax.vlines([-T, T], 0, 0.4, color='g', lw=2)
x_le_T, x_ge_T = x[x<-T], x[x>T]
ax.fill_between(x_le_T, t.pdf(x_le_T), np.zeros(len(x_le_T)), alpha=0.3, color='b')
ax.fill_between(x_ge_T, t.pdf(x_ge_T), np.zeros(len(x_ge_T)), alpha=0.3, color='b')

p = 1 - (t.cdf(T) - t.cdf(-T))
ax.set_title(r'$P(\left | T \right | \geqslant {:.3}) = {:.3}$'.format(T, p));

, p-value 27%, .. , - , \ alpha = 0.05, p-value , 5 . , , - , \ alpha, 0.95:





\ textrm {CI} _ {1 - \ alpha} = \ bar {x} \ pm \ left (t _ {\ frac {\ alpha} {2}, \ textrm {df}} \ right) \ left (\ frac { s} {\ sqrt {n}} \ right)

SciPy, interval loc () scale () :





sample_loc = sample.mean()
sample_scale = sample.std(ddof=1)/10**0.5
ci = stats.t.interval(0.95, df=9, loc=sample_loc, scale=sample_scale)
ci
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    
(76.50640345566619, 90.89359654433382)

, \ bar {x} = 83.7, , \ alpha = 0.95 [76.5; 90.9]. , , \ bar {x}, .





, , , ( ). , , t- , t- , t- .





Of course, I would like to insert some gif at the end, but I want to end with the phrase of Herbert Spencer: " The greatest goal of education is not knowledge, but action ", so launch your anacondas and take action ! This is especially true for self-taught people like me.





I press F5 and look forward to your comments!







More articles:


All Articles