Ask Ethan: What is the fundamental reason for E = mc²?

Albert Einstein in 1920. Although he made many breakthroughs in physics, from special and general relativity to the photoelectric effect and statistical mechanics, he was unable to solve many problems. His most famous equation remains E = mc².



Ask any person, even not versed in science, about Einstein's achievements, and you will be given an example of his most famous equation: E = mc². In simple terms, it means that energy is equal to mass times the square of the speed of light. And this says a lot about our Universe. The only equation tells how much energy is contained in a massive particle at rest, and how much energy is required to create particles and antiparticles. It tells us how much energy is released in nuclear reactions, and how much energy is generated by the annihilation of matter with antimatter.



But why? Why is energy equal to mass times the speed of light squared? Why not in some other way? Our reader asks about this:



Einstein's equation is stunningly elegant. But is its simplicity real, or does it just seem? Is it derived directly from the equivalence of the energy of any mass and the square of the speed of light (and this generally seems to be an amazing coincidence)? Or does it only exist because its members are defined in a convenient way?



Great question. Let's explore Einstein's most famous equation and see why it couldn't be different.





Preparing for Testing a Nuclear-Powered Rocket, 1967. It works by converting mass into energy, based on the famous equation E = mc².



First you need to understand something about energy. It is very difficult to define it, especially for a person who is far from physics. We can think of a few examples offhand.

• , .. , . , , . , , , . , , .
• , .
• – , .
• , , .

And, of course, many other types. Energy is one of those "we know when we see" things. But physicists need a more universal definition. One of the best is that energy recovered or recovered is a quantification of our ability to do work.







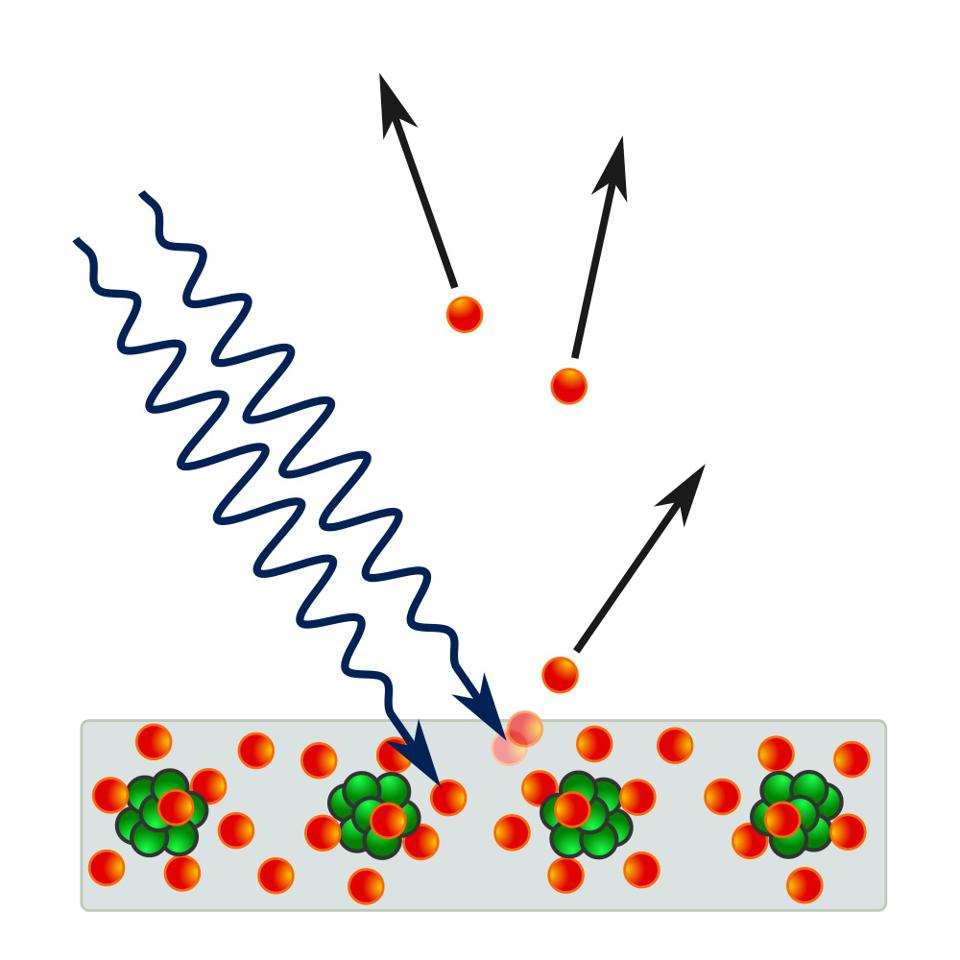
The photoelectric effect describes the ionization of electrons by photons depending on the wavelengths of individual photons, and not on the intensity of light, total energy, or any other property. If a quantum of light has enough energy, it can interact with an electron, ionizing it, knocking it out of the material, which will give a detectable signal. These photons carry energy and do work on the electrons they hit.



The work has its own physical definition: it is the force applied in the direction coinciding with the direction of movement of the object, multiplied by the distance of its movement. Raising the bar to a certain height requires work to be done against the force of gravity, and increases the gravitational potential energy. Letting go of the bar, we transform its gravitational potential energy into kinetic energy. The barbell striking the floor converts kinetic energy into a combination of thermal, mechanical and sound energy. Energy in these processes is not created or destroyed, but is transformed from one form to another.



Most people think of the E = mc² formula in terms of dimensional analysis. They say: so, energy is measured in joules, and a joule is a kilogram per meter squared per second squared. Therefore, to convert mass into energy, you need to multiply this by a meter squared, divided by a second squared. At the same time, we have a fundamental constant with a meter / second dimension. This reasoning is reasonable, but not sufficient.





Photos from Trinity, the world's first nuclear weapons technology test. The situation is shown 16, 25, 53 and 100 ms after ignition. The highest temperature is reached at the very beginning of the explosion, before its volume grows many times over.



After all, you can measure any speed in meters per second, not just the speed of light. In addition, no one forbids nature to give out a proportional constant - some factor like ½, ¾, 2π, etc., to make the equation true. To understand why the equation should look like E = mc², and why there can be no other options, we need to imagine a physical situation in which different interpretations can be distinguished. Such a theoretical tool is known as a "thought experiment" (or gedankenexperiment, as Einstein would say) and became one of the great ideas that emerged in Einstein's head and ingrained in the scientific mainstream.



We can imagine that a particle has energy inherent in its rest mass, and the energy of its motion is kinetic. It can be imagined that the particle began its path, being high in the gravitational field, that is, with a large supply of potential energy, but initially did not move. If we drop it, the potential energy will turn into kinetic energy, and the rest mass energy will remain the same. Before the very impact on the ground, she will not have any potential energy - only kinetic and rest mass energy, whatever they may be.







The orange-colored particle resting above the earth's surface will not have kinetic energy, but will have a large supply of potential. If it is sent into free fall, it will acquire kinetic energy, into which potential energy will turn.



Now let's add another idea: that all particles have antiparticle counterparts, and that when they collide with each other, they annihilate, releasing pure energy.



Yes, E = mc² describes the relationship between mass and energy, including the amount of energy required to create particle-antiparticle pairs from nothing, and how much energy you get when that pair annihilates. But we don't know yet, we want to prove it!



Let's imagine that we have not one particle high in the gravitational field, but both a particle and an antiparticle, and they are ready to fall. Consider two different development scenarios and explore their implications.







The appearance of particle-antiparticle pairs (left) from pure energy is a completely reversible reaction (right), they can annihilate, turning into energy. But for many particle systems, reversibility is not guaranteed.



Scenario 1: both particle and antiparticle fall and annihilate just before hitting the ground. The situation is similar to the one described earlier, we just doubled it. Both particle and antiparticle started with a certain amount of rest mass energy. We do not know how much there was, we just know that the particle and the antiparticle have the same, since the masses of the particles are identical to the masses of the corresponding antiparticles.



They now both fall, converting potential gravitational energy into kinetic energy, in addition to their rest mass energy. As in the previous case, before hitting the ground, all their energy is contained in two forms - energy of rest mass and kinetic energy. Only now, just before the collision, they annihilate, turning into two photons, the total energy of which should be equal to the sum of the rest mass energies and the kinetic energies of both particles.



However, for a photon that has no mass, the energy is described by only one momentum multiplied by the speed of light: E = pc. Whatever the energy of both particles before colliding with the earth, the energy of these photons should add up to the sum of the energy of the particles.







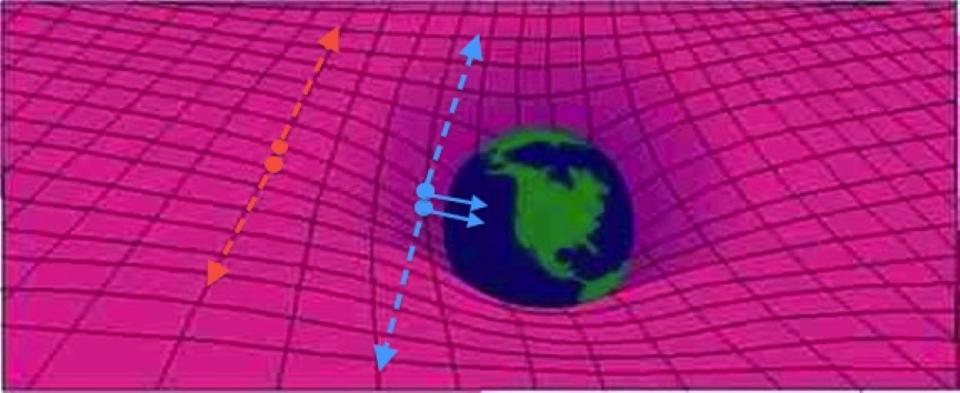
If a particle-antiparticle pair annihilates into pure energy (two photons), having a lot of gravitational potential energy in stock, then only the rest mass (orange) will go into the photon energy. If you level these particles down so that they annihilate just before impact, they have more energy, resulting in more blue photons.



Scenario 2: a particle and an antiparticle annihilate into pure energy, and then fall down to the ground in the form of photons with zero rest mass. Then all their rest mass energy will turn into the energy of photons.



It turns out that in this case the total energy of these photons, each of which has an energy E = pc, should be equal to the sum of the energies of the rest masses of the particle and the antiparticle.



Now let's imagine that these photons reached the surface of the planet, and after that we measure their energy. According to the conservation law, their energy should be equal to the energy of the photons from the first scenario. This means that the photon must gain energy falling in the gravitational field. This phenomenon is known as gravitational blue shift. In addition, this implies the idea that the rest mass of a particle should be equal to E = mc².







When a quantum of radiation leaves the gravitational field, its frequency must undergo a red shift in order for the energy to be conserved. When falling, the frequency should shift to the blue range. This only makes sense if gravity is related not only to mass, but also to energy. Gravitational redshift is one of the key predictions of Einstein's General Theory of Relativity. But it was only recently tested in an environment with fields as strong as the center of our Galaxy.



There is only one definition of energy that applies to all particles, mass and mass, and satisfies scenarios 1 and 2, which should give the same results. E = √ (m ² c ⁴ + p ² c ²). Let's see what happens to him in different situations.

• For a massive particle at rest and without an impulse, the energy will be equal to √ (m ² c ⁴ ), that is, E = mc².
• A massless particle must move, and its rest mass is zero. Its energy is √ (p²c²), or E = pc.
• For a massive particle moving much slower than the speed of light, the momentum can be written as p = mv, and then its energy becomes equal to √ (m²c ⁴ + m²v²c²). This can be rewritten as E = mc² * √ (1 + v² / c²) if v is significantly less than c.

If you are unfamiliar with the last term, do not be discouraged. If v is very small compared to c, you can do the Taylor expansion, and you get E = mc² • [1 + ½ (v² / c²) + ...]. Taking the first two terms, you get E = mc² + ½mv²: rest mass plus the good old nonrelativistic formula for kinetic energy.







Above: The photon is moving inside the box. Middle: The box has absorbed a photon. Bottom: The photon is re-emitted in the opposite direction. From such an experiment, accepting the laws of conservation of energy and momentum, one can deduce the famous E = mc².



Of course, you shouldn't write E = mc² like that, but this is my favorite way of illustrating this problem. I can recommend three more ways of illustration, as well as a description of how Einstein himself did it. My second favorite illustration of the derivation of this formula will be the consideration of a photon moving in a stationary box with a mirror on one of the walls.



When a photon collides with a mirror, it is absorbed for a while, as a result of which the box must acquire some energy, and start moving in the same direction as the photon - this is the only way to conserve energy and momentum.



After re-emitting the photon moves in the opposite direction, so the box (which has lost a little mass after re-emitting the photon) needs to move forward even faster.



And although there are many unknowns, in such a situation you can write many equations that need to be matched. The total energy of all parts of the system and the total moment must be equivalent. If you solve these equations, you get only one definition of the energy of the rest mass: E = mc².







Einstein displays the Special Theory of Relativity in front of the audience, 1934. If we require conservation of energy and apply the theory of relativity to suitable systems, it is necessary that E = mc².



One can imagine a completely different universe from which we live. Perhaps, energy is not stored there - and then the formula E = mc² may not be a universal expression of rest mass. Perhaps we could violate the law of conservation of momentum - then our definition of total energy, E = √ (m ²c ⁴ + p ² c ² ) would not be true. And if the General theory of relativity did not work there, or the momentum and energy of the photon would not be related by the relation E = pc, then E = mc² would not be a universal formula for massive particles.



But in our Universe, energy is conserved, and the General Theory of Relativity works. Therefore, you just need to choose suitable experimental conditions. And even without actually conducting it, one can come to only one consistent value for the energy of the rest mass of a particle. One can imagine a universe in which the relationship of mass and energy would be different, but it would be completely different from ours. And it's not just a convenient definition - it's the only way to conserve energy and momentum with the laws of physics we have.