🛤️ 👩🏾‍💻 🍰 Matrix-Rematrix 🔦 🐑 🤘

The work of a neural network is based on matrix manipulation. For training, a variety of methods are used, many of which have grown out of the gradient descent method, where it is necessary to be able to handle matrices, to calculate gradients (derivatives with respect to matrices). If you look under the hood of a neural network, you can see chains of matrices, which often look intimidating. Simply put, “the matrix is waiting for us all”. It's time to get to know each other better.

To do this, we will take the following steps:

Let's consider manipulations with matrices: transposition, multiplication, gradient;
;
.

NumPy . , , , , . , , , - , , , . , - : , .

-

- , , , . , , , Google TensorFlow.

, , , , , $a_ {i}$ , i = 0, 1, 2, ..., n-1 ; - .

import numpy as np #   numpy
a=np.array([1,2,5])
a.ndim #  ,   = 1
a.shape #      (3,)
a.shape[0] #      = 3

$a_ {i} \ cdot b_ {i} = a_ {0} \ cdot b_ {0} + a_ {1} \ cdot b_ {1} + a_ {2} \ cdot b_ {2}$ . , , 0 2 .

b=np.array([3,4,7])
np.dot(a,b) #   = 46
a*b #   array([ 3,  8, 35])
np.sum(a*b) # = 46

( ) - , $A_ {i, j}$ . , $A_ {0, 2}$ - 0- 2- . , .

A=np.array([[ 1,  2,  3],
            [ 2,  4,  6]])
A # array([[1, 2, 3],
  #        [2, 4, 6]])
A[0, 2] #    ,    = 3
A.shape # (2, 3)   2 , 3

C = AB , $C_ {i, k} = A_ {i, j} B_ {j, k}$ . , ( )

B=np.array([[7, 8, 1, 3],
            [5, 4, 2, 7],
            [3, 6, 9, 4]])
A.shape[1] == B.shape[0] # true
A.shape[1], B.shape[0] # (3, 3) 
A.shape, B.shape # ((2, 3), (3, 4))
C = np.dot(A, B)
C # array([[26, 34, 32, 29],
  #        [52, 68, 64, 58]]); 
  #  , C[0,1]=A[0,0]B[0,1]+ A[0,1]B[1,1]+A[0,2]B[2,1]=1*8+2*4+3*6=34
C.shape # (2, 4)

, :

np.dot(B, A) # ValueError: shapes (3,4) and (2,3) not aligned: 4 (dim 1) != 2 (dim 0)

, .

, . , $a_ {i, 0}$ $b_ {j, 0}$ . $D_ {i, j} = a_ {i, 0} b_ {j, 0}$ . , , , $b_ {j, 0} = (bT) _ {0, j}$ , - ( NumPy). $D = a \ cdot bT$ . , $DT = (a \ cdot bT) .T = (bTT) \ cdot aT = b \ cdot aT$ .

a = np.reshape(a, (3,1)) #   ,  a.shape = (3,)  (3,1),
b = np.reshape(b, (3,1)) #  ,  
D = np.dot(a,b.T)
D # array([[ 3,  4,  7],
  #        [ 6,  8, 14],
  #        [15, 20, 35]])

, . , .

, , . (cost function). , . . , (learning rate), , (epoch). , . (), . . , , , .

, ( , ).

- (samples) . . , (), ( ) - (samples), - (features).

, ( ). (, …) , , . , .

!

, , . , “ ” . , , . , , . , , , .

, 10 . , (10, 3). “ ”, . , . , :

, , 0 50 ;

X=np.random.randint(0, 50, (10, 3))

0 1;

X=np.random.rand(10, 3)

$\ mu = 2$ $\ sigma ^ 2 = 16$ . , , $N (\ mu, \ sigma ^ 2)$ ;

X=4*np.random.randn(10, 3) + 2

$\ mu = 0$ $\ sigma = 1$ , .

, (10, 3) $W ^ {(1)}$ , . , , . , , , $W ^ {(1)}$ (3, 4) . , $(10, 3) (3, 4) \ Rightarrow (10, 4)$ . , $X \ cdot W ^ {(1)}$ (10.4) , - - , . . , (m, n) ( , ) $a_ {i, j}$ , f (A) , $f (a_ {i, j})$ ; , , $a_ {1,2} \ Rightarrow f (a_ {1,2})$ , . , $W ^ {(2)}$ , (4, 1) . , $(10, 3) (3, 4) (4, 1) \ Rightarrow (10, 1)$ . , $\hat{Y}$ 10- (samples) . :

$\hat{Y}=X\cdot W^{(1)}\cdot W^{(2)}, \quad\quad \hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}.$

, . (bias).

. : , , , .

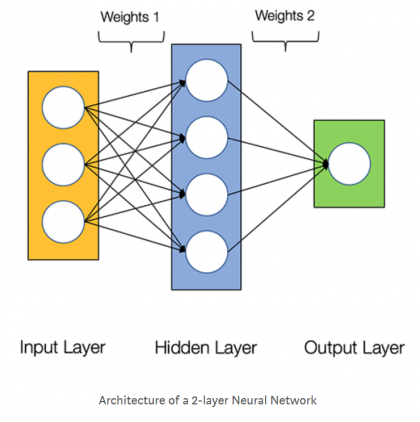
X=np.random.randint(0, 50, (10, 3))
w1=2*np.random.rand(3,4)-1 #       -1  +1
w2=2*np.random.rand(4,1)-1
Y=np.dot(np.dot(x,w1),w2) #   
Y.shape # (10, 1)
Y.T.shape # (1, 10)
(np.dot(Y.T,Y)).shape # (1, 1), ,

. -1 +1, “” ( ).

. f_1 “ ”, - .

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)}),$ $\hat{Y}=f_2(f_1(X \cdot W^{(1)})\cdot W^{(2)}).$

, .

$\triangle=\sum_i(Y_{i,0}-\hat{Y}_{i,0})^2=\sum_i\widetilde{Y}_{i,0}^2=(\widetilde{Y}.T)_{0,i}\widetilde{Y}_{i,0}=(\widetilde{Y}.T)\cdot\widetilde{Y},$

(X,Y) - , $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ . , $(\widetilde{Y}.T)_{0,i}=\widetilde{Y}_{i,0}$ .

, . .

. - . , . , .

- , . f(x) $f^{'}(x_0)=0$ , “ ” - . , , . , , . : - , , - . (, 16 ), , . . , $f^{'}(W)<0$ , , , $f^{'}(W)>0$ , . , .

$W\Rightarrow W+\mu\cdot\delta W=W-\mu\cdot\frac{\partial \triangle}{\partial W},$

$W_{i,j}\Rightarrow W_{i,j}+\mu\cdot\delta W_{i,j}=W_{i,j}-\mu\cdot\frac{\partial \triangle}{\partial W_{i,j}},$

$\mu$ - (learning rate). , . . - , , . , - .

.

$\frac{\partial a_{m, n}}{\partial a_{i,j}}=\delta_{m,i}\delta_{n,j},$

$\delta_{i,j}$ - , , i=j . , $\delta_{1,1}=1$ , $\delta_{2,1}=0$ . : .

$\frac{\partial \triangle}{\partial W_{m,n}}=-2\sum_i(Y_{i,0}-\hat{Y}_{i,0})\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}},$

, , $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ , .

. . , , .

, $\hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}$ ,

$\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,k}^{(1)}\delta_{k,m}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,m}^{(1)}=-2\widetilde{Y}_{i,0}(X\cdot W^{(1)})_{i,m}$

, $A_{i,m}=(A.T)_{m.i}$ . , :

$\delta W_{m,0}^{(2)}=-\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=2((X\cdot W^{(1)}).T)_{m,i}\widetilde{Y}_{i,0},$

$\delta W^{(2)}=2((X\cdot W^{(1)}).T)\cdot \widetilde{Y}.$

, , , $\delta W^{(2)}$ . $X\cdot W^{(1)}$ (10,3)(3,4)=(10,4) , - (4,10) . $\widetilde{Y}$ $\hat{Y}$ - (10,1) . , $\delta W^{(2)}$ (4,10)(10,1)=(4,1) , .

deltaW2=2*np.dot(np.dot(X,w1).T,Y)
deltaW2.shape # (4,1)

$W^{(1)}$ .

$\frac{\partial \triangle}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}X_{i,j} \delta_{j,m}\delta_{k,n}W_{k,0}^{(2)}=-2\widetilde{Y}_{i,0}X_{i,m} W_{n,0}^{(2)}=-2(X.T)_{m,i}\widetilde{Y}_{i,0}(W^{(2)}.T)_{0,n},$ $\delta W^{(1)}=2(X.T)\cdot \widetilde{Y}\cdot (W^{(2)}.T).$

, “ ”, “ ” - . , , . : “” ( ), , .

$\delta W^{(1)}$ : (3,10)(10,1)(1,4)=(3,4) .

. ,, , , . . , . , . , , : z=f(y(x)) , $z_x^{'}=f_y^{'}y_x^{'}$ .

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)})\quad\Rightarrow\quad \hat{Y}_{i,0}=f_2(C_{i,0}),$

$C_{i,0}=B_{i,k}W_{k,0}^{(2)}, \quad\quad B_{i,k}=f_1(A_{i,k}), \quad\quad A_{i,k}=X_{i,j} W_{j,k}^{(1)}.$

W_2 , . ,

$\delta W_{m,0}^{(2)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}\frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})\delta_{i,\mu}B_{\mu,k}\delta_{k,m}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})B_{i,m}.$

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}=f_2^{'}(C_{i,0})\delta_{i,\mu}, \quad\quad \frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\frac{\partial W_{k,0}^{(2)}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\delta_{k,m}.$

, - . : $B_{i,m}=(B.T)_{m,i}$ , $f_1(A_{i,m})=(f_1(A).T)_{m,i}$ . ,

$\delta W_{m,0}^{(2)}=2(B.T)_{m,i}\widetilde{Y}_{i,0}f_2^{'}(C_{i,0}) \Rightarrow \delta W^{(2)}=2(B.T)\cdot(\widetilde{Y}*f_2^{'}(C))$

“*” . , , , a*b , ; , $a_{1,2}b_{1,2}$ .

. f_1(x)=x^2 f_2(x)=x^3 . , , . NumPy .

def f1(x): #  
    return np.power(x,2)
def graf1(x): # 
    return 2*x
def f2(x): #  
    return np.power(x,3)
def gradf2(x): # 
    return 3*np.power(x,2)

A=np.dot(X,w1) #   
B=f1(A)        #   
C=np.dot(B,w2) #    
Y=f2() #   
deltaW2=2*np.dot(B.T, Y*gradf2(C))
deltaW2.shape # (4,1)

$W^{(1)}$ , . - .

$\delta W_{m,n}^{(1)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}\frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}},$

$C_{\mu,\nu}=B_{\mu,k}W_{k,\nu}^{(2)}$ . :

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}=f_2^{'}(C_{i,0})\delta_{i,\mu}\delta_{0,\nu},\quad\quad \frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}=\delta_{\mu,l}\delta_{k,s}W_{k,\nu}^{(2)},\quad\quad$ $\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}}=\frac{\partial B_{l,s}}{\partial A_{r,e}}\frac{\partial A_{r,e}}{\partial W_{m,n}^{(1)}}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,e}\delta_{j,m}\delta_{e,n}X_{r,j}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,n}X_{r,m}.$

$\ delta W_ {m, n} ^ {(1)} = 2 \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) \ delta_ {i, \ mu} \ delta_ {0, \ nu} \ delta _ {\ mu, l} \ delta_ {k, s} W_ {k, \ nu} ^ {(2)} f_1 ^ {'} (A_ {l, s}) \ delta_ { s, n} \ delta_ {l, r} X_ {r, m} = 2 \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) W_ {n, 0} ^ {(2)} f_1 ^ {'} (A_ {i, n}) X_ {i, m},$

$\ delta_ {i, \ mu} \ delta_ {0, \ nu} \ delta _ {\ mu, l} \ delta_ {k, s} \ delta_ {s, n} \ delta_ {l, r} = \ delta_ {i , l} \ delta_ {i, r} \ delta_ {k, n} \ delta_ {s, n}.$

, $\ delta_ {0, \ nu} W_ {k, \ nu} ^ {(2)} = W_ {k, 0} ^ {(2)}$ , , “”, l, r, k, s .

“” ,

$\ delta W_ {m, n} ^ {(1)} = 2 (XT) _ {m, i} \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) ( W ^ {(2)}. T) _ {0, n} f_1 ^ {'} (A_ {i, n}),$ $\ delta W ^ {(1)} = 2 (XT) \ cdot [[(\ widetilde {Y} * f_2 ^ {'} (C)) \ cdot (W ^ {(2)}. T)] * f_1 ^ {'} (A)].$

, $D_ {i, o} = \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) \ Rightarrow \ widetilde {Y} * f_2 ^ {'} (C)$ , $F_ {i, n} = D_ {io} (W ^ {(2)}. T) _ {0, n}$ , $F_ {i, n} f_1 ^ {'} (A_ {i, n}) \ Rightarrow F * f_1 ^ {'} (A)$ .

deltaW1=2*np.dot(X.T, np.dot(Y*gradf2(C),w2.T)*gradf1(A))
deltaW1.shape # (3,4)

. .

“, - . -!” ? , , , . , . - , , . ! , , - . , , .

, . James Loy - , , , , , . . , , , . “-”, , , . , TensorFlow Keras. , the original source (there is a translation into Russian).

Write codes, delve into formulas, read books, ask yourself questions.

As for the tools, it is Jupyter Notebook ( Anaconda rules!), Colab ...

Matrix-Rematrix

-

!

.

More articles: