Part 1. Introduction
Part 2. Balancing and insertion
This is part 2 of the Understanding Red-Black Tree series. If you missed the first part, I highly recommend checking it out here . There we sorted out the reason for the appearance of cchd and put some of its properties on the shelves.
In this part we will discuss insertion and balancing. These things go side by side, without balancing the tree will lose its properties, and there will be little sense from it.
Keeping in mind that kchd is a 2-3 tree (sometimes I will remind you of this), we will immediately start with its construction. But some clarifications are still needed now.
All inserted nodes, except for the root of the tree, are inserted with red color. This is explained by the fact that we always first add a value to an already existing node and only after that we do balancing (remember the situation with the resulting 4-nodes).
In the first part, we found out that we are disassembling a left-sided red-black tree , from this it follows that red nodes can only lie on the left (the opposite case requires balancing).
Let's also deal with the three operations that we need when balancing. I ask you not to think about them now and delve into more details already during the construction of the tree. I will provide a description of them here so that they do not interfere later :)
- . , , -. , . - .
, . , .
( )
. .
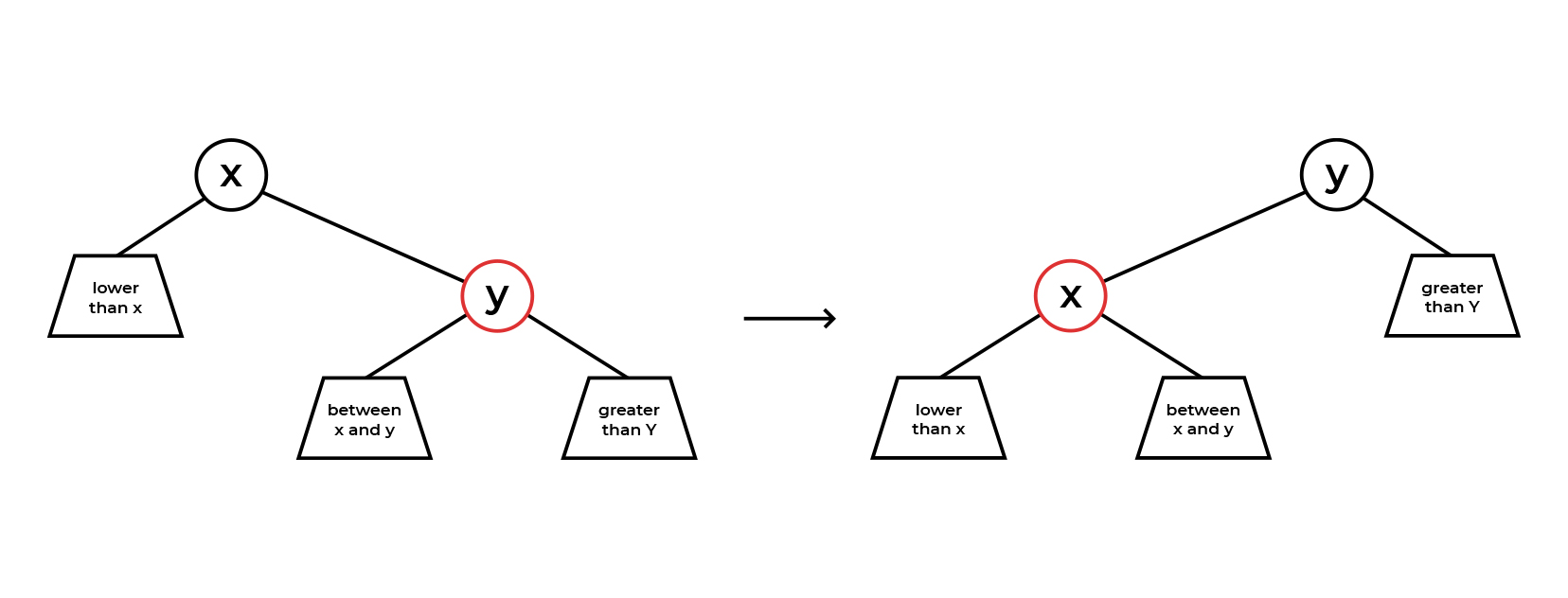
, parentNode ( parentNode - x, childNode - y) childNode, . ! , , childNode , parentNode , ( , childNode - , , parentColor = RED, ). "" childNode (, tempNode). , . , childNode, parentNode, childNode, , (/) parentNode, parentNode .
( )
, . .
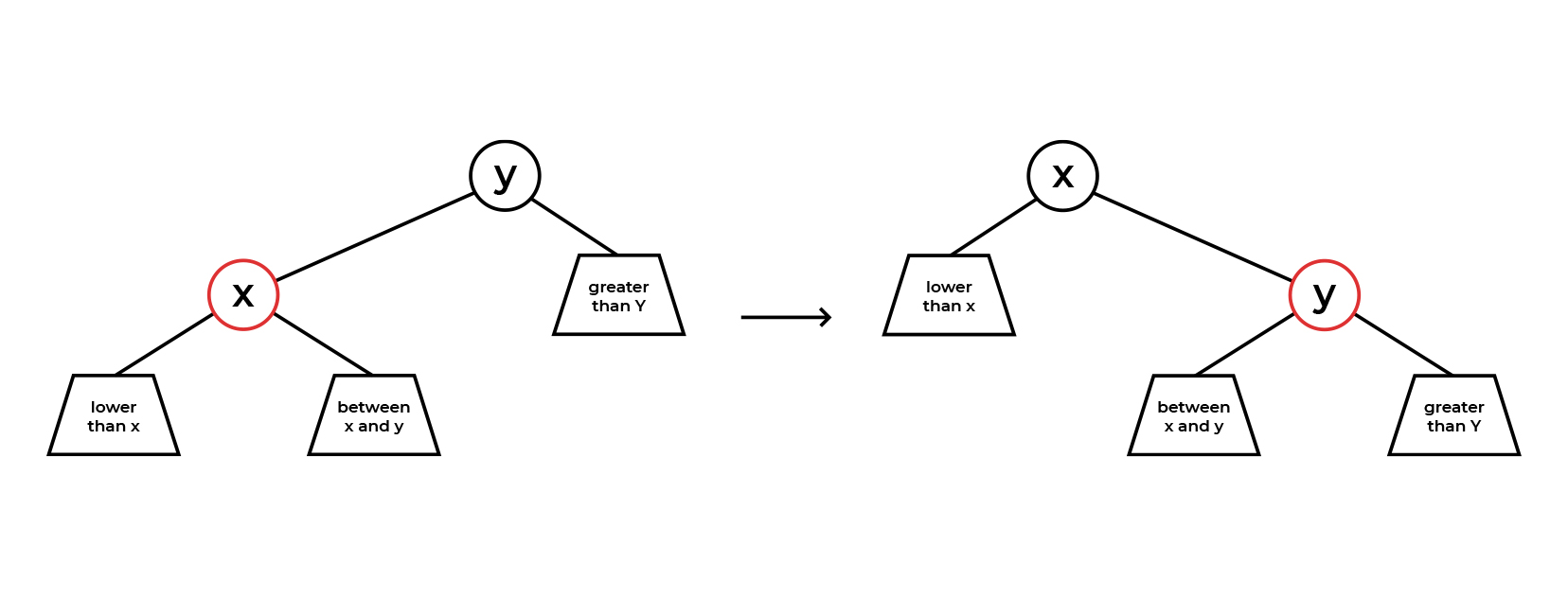
, parentNode . , parentNode - . , .
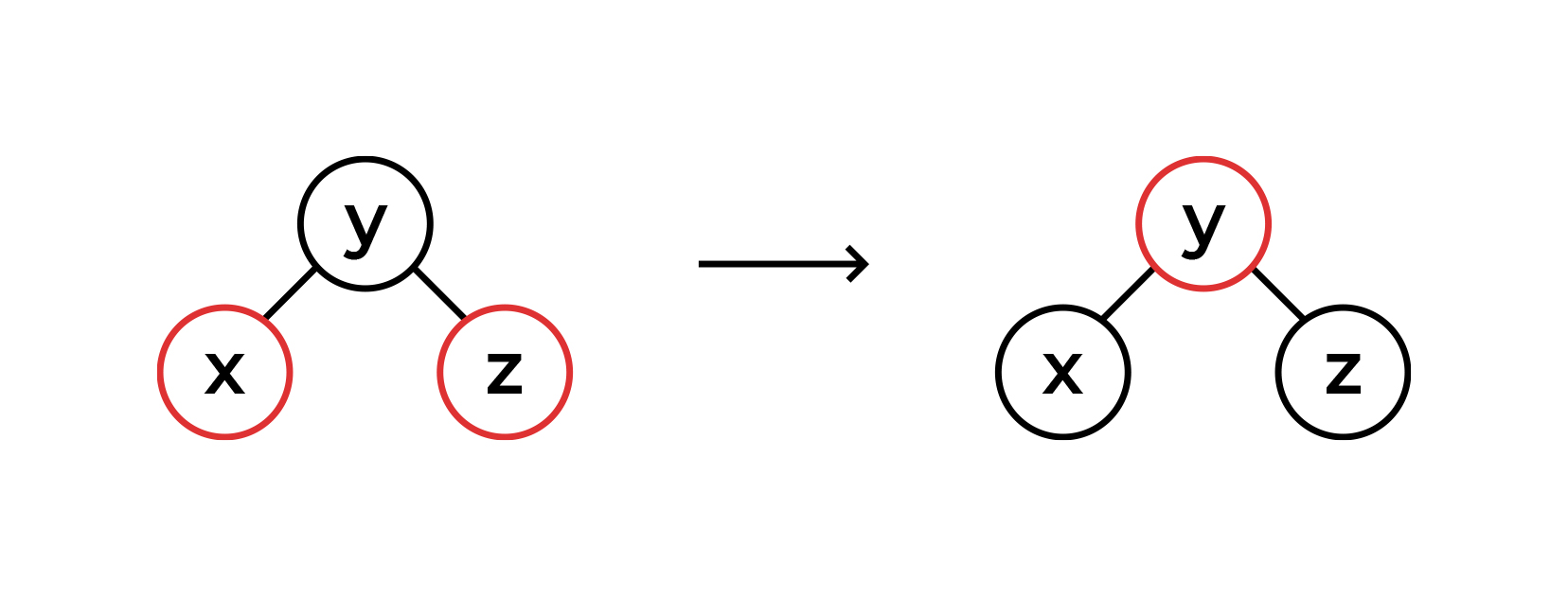
, ( , ), parentNode! ( ). .
- .
, .
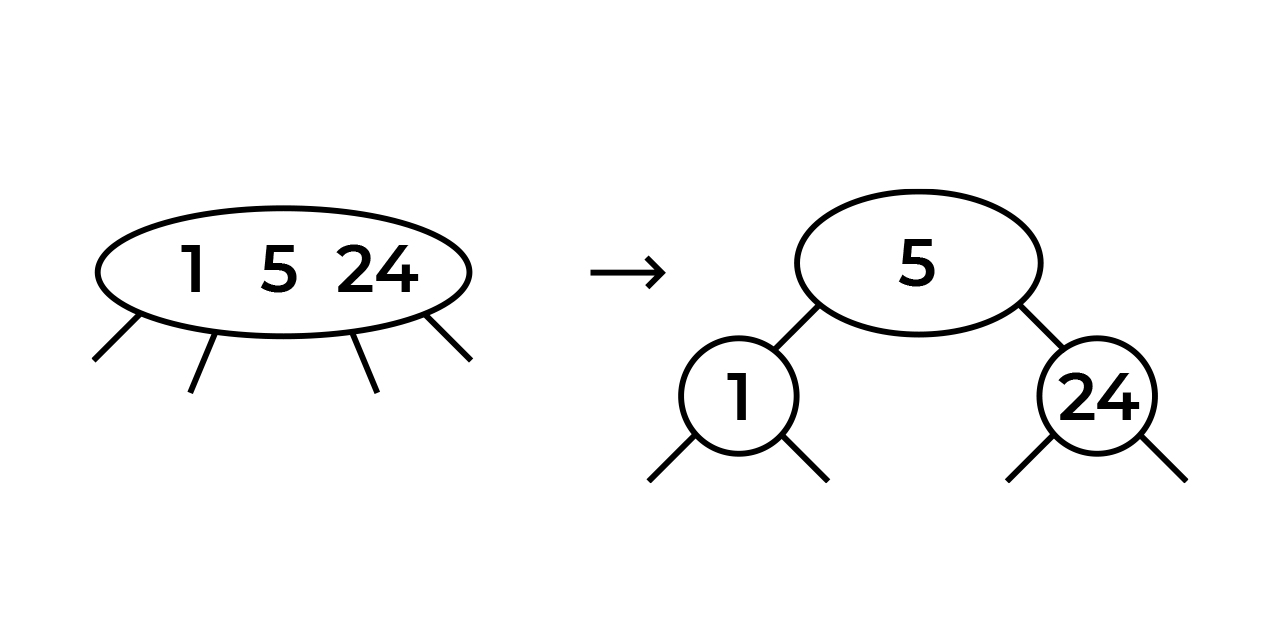
24. . , , .
, , 5. , .
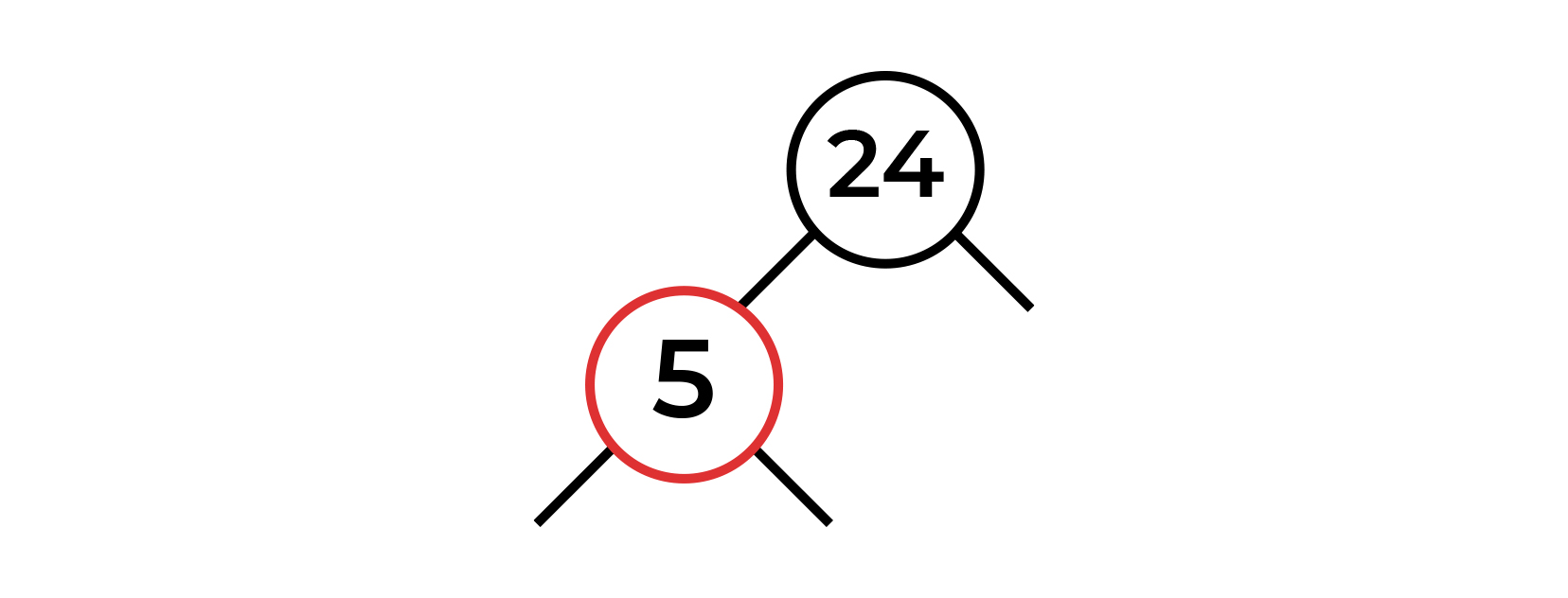
1 5. . , !
, - ( ). . - . , - . \ . , .
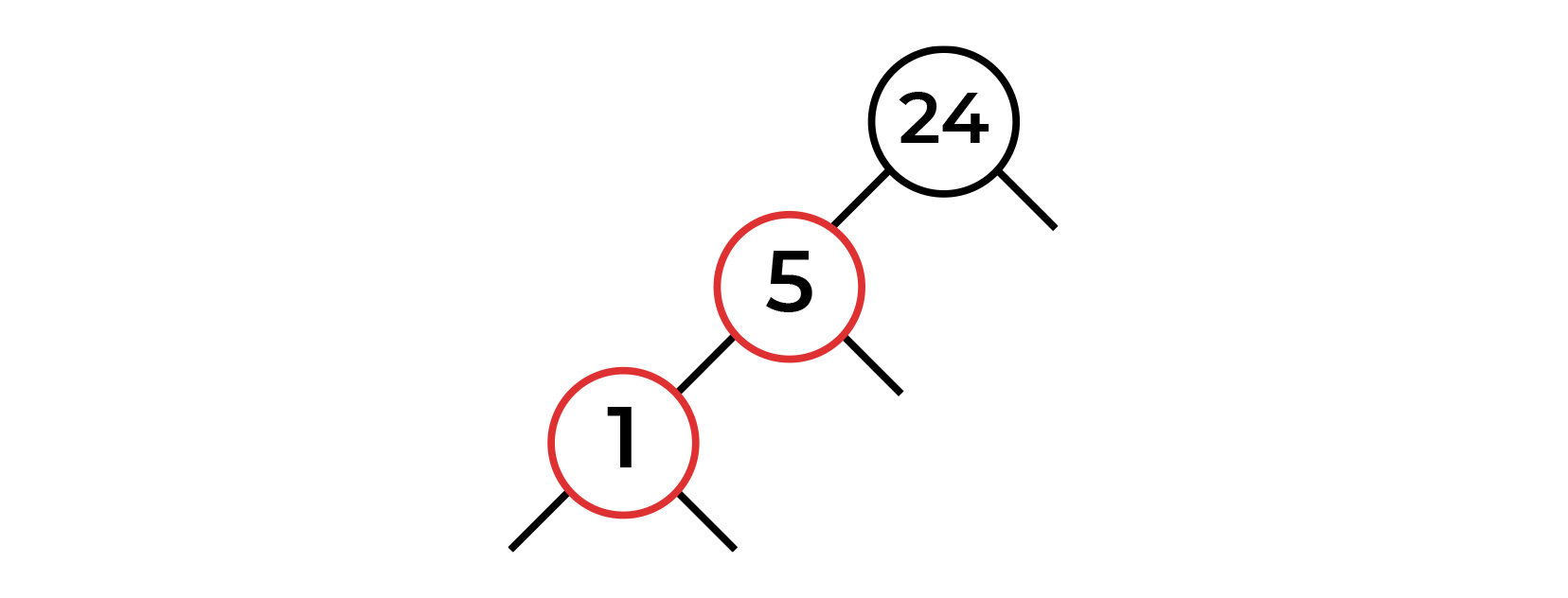
. , , , .
, 3 : , , .
1 , . . 5 - , ( ). 24 , , .
. - . , . - 24. .
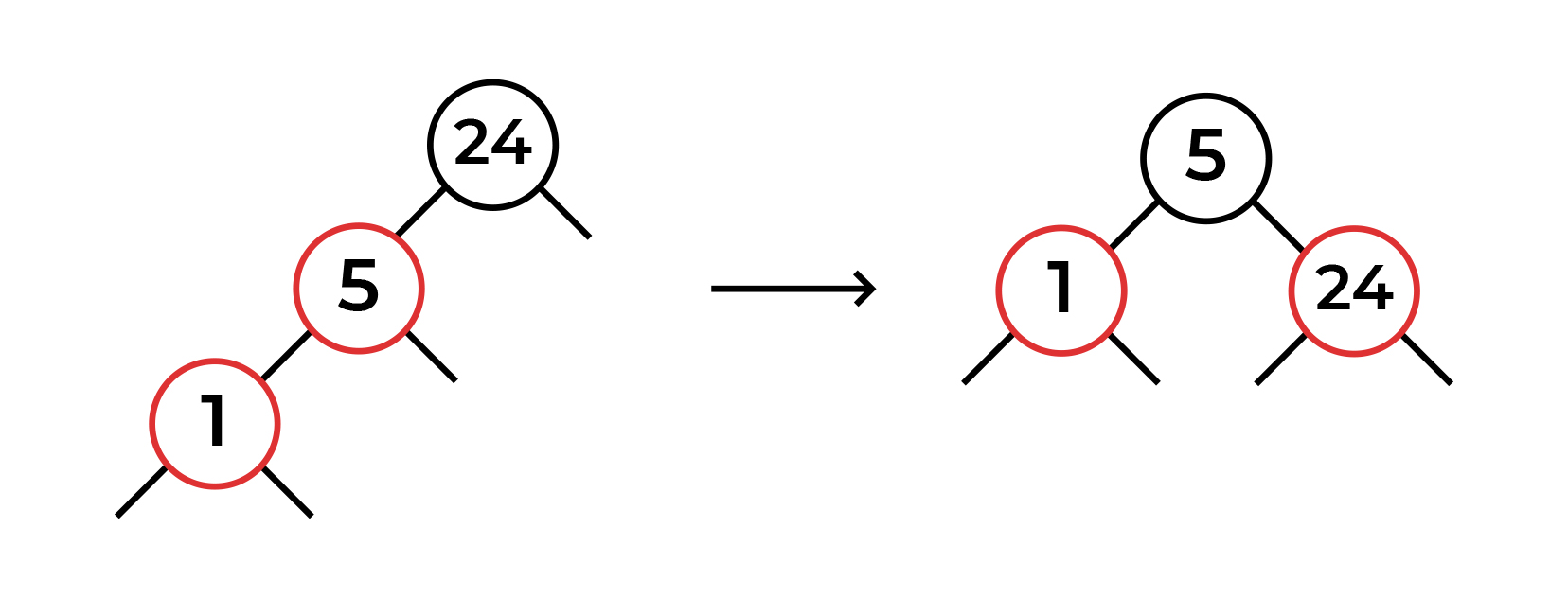
, . ! . ( 24 , , )
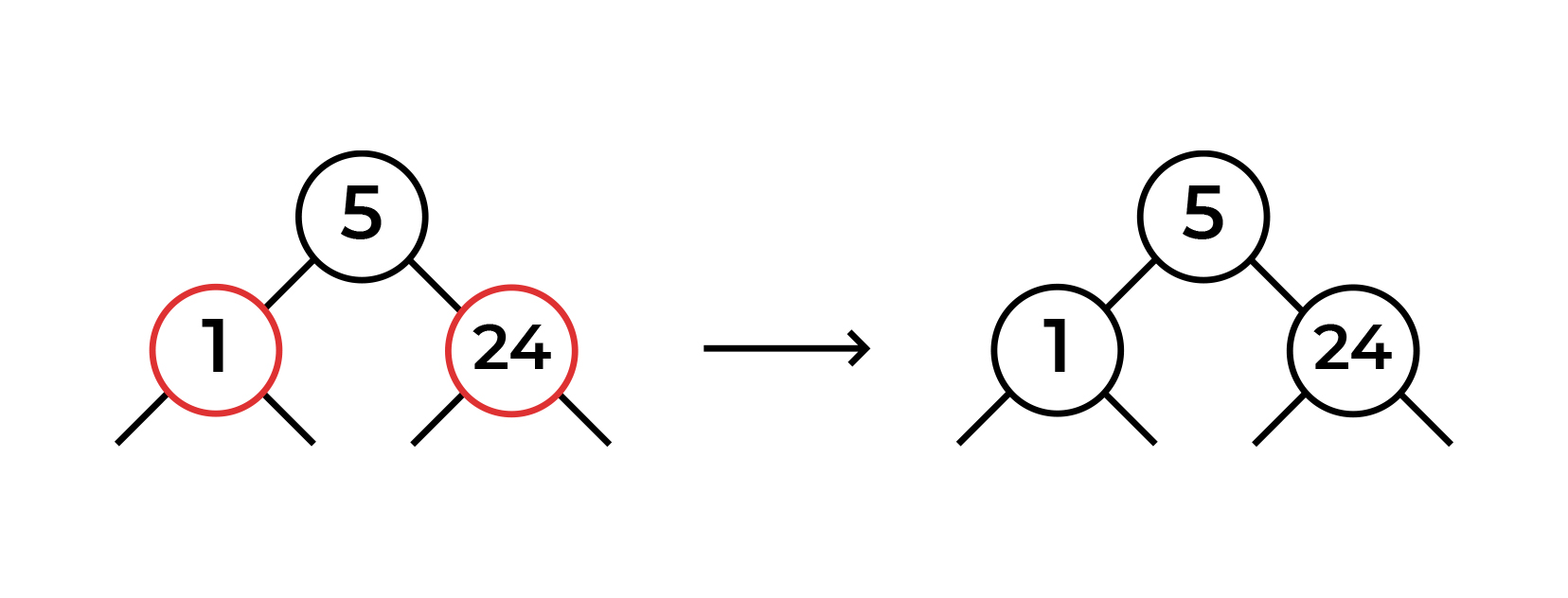
( )! 2-3 .
, 2-3 ("" + ), , :) , , 2-3 , - , , "" .
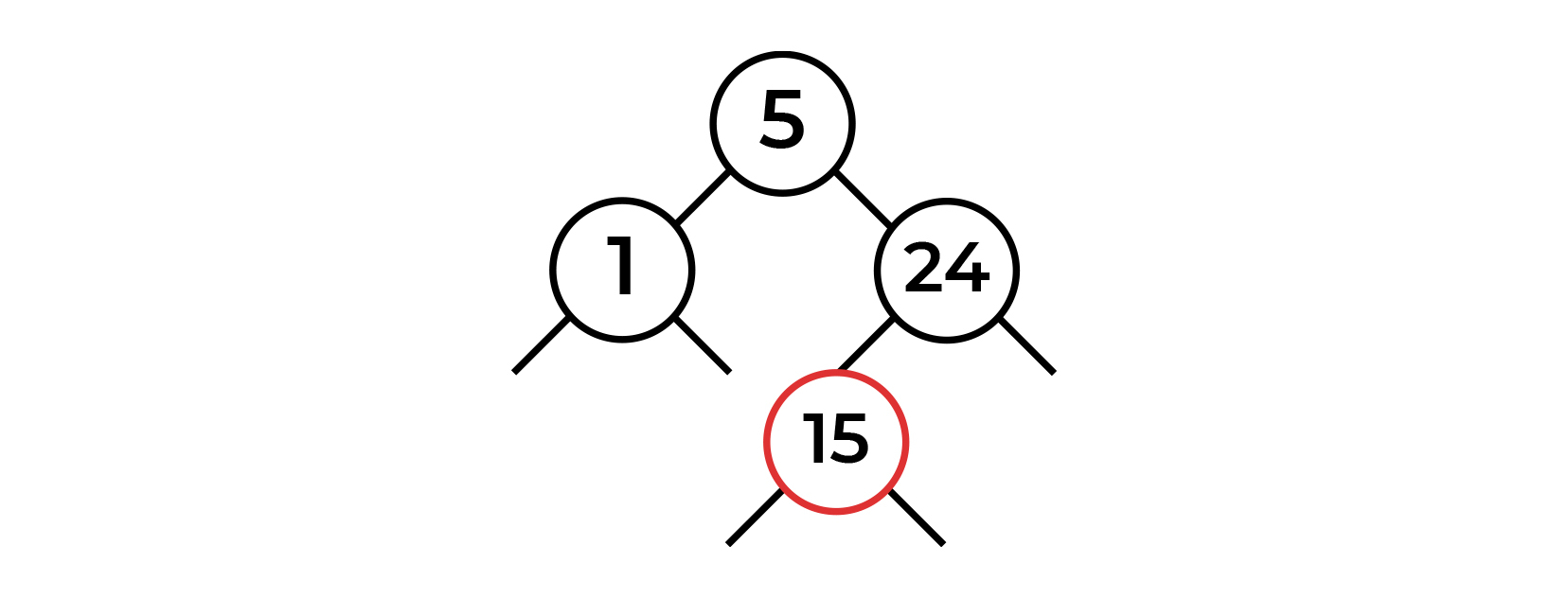
. 15. 24. .
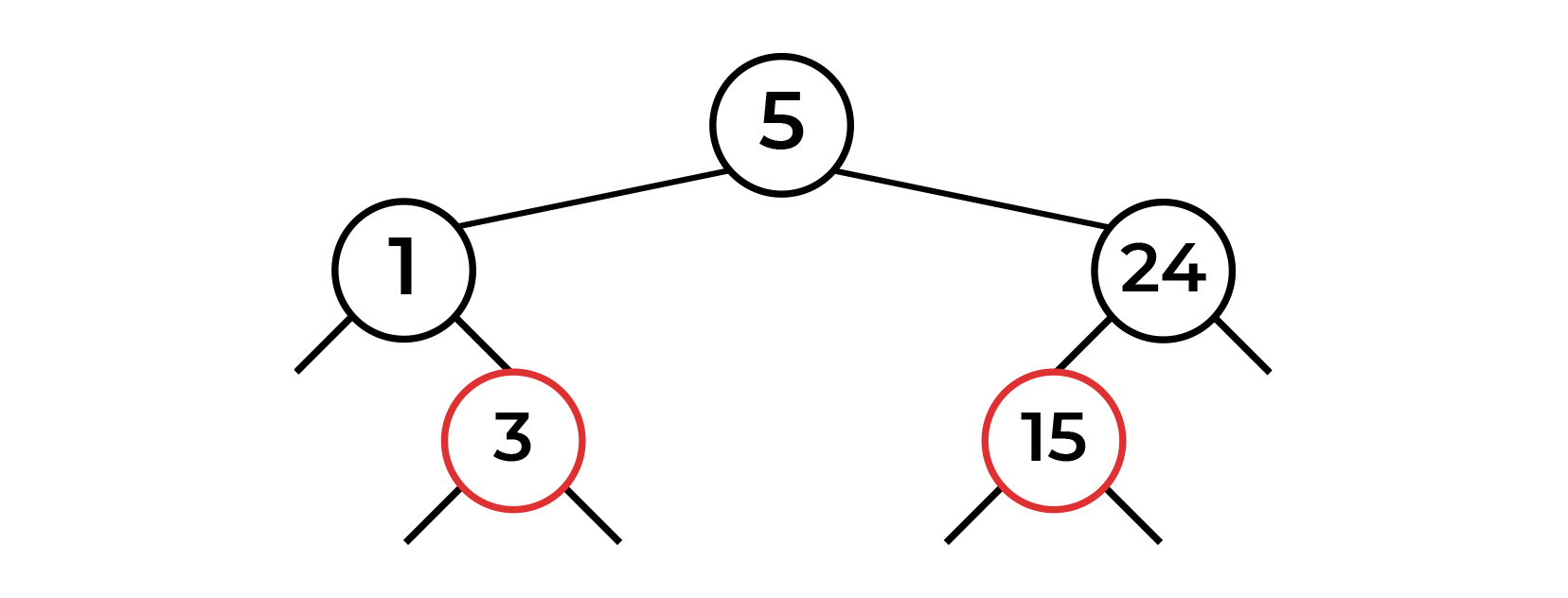
3. , 1, -1.
, . . + . ( , , ). , .
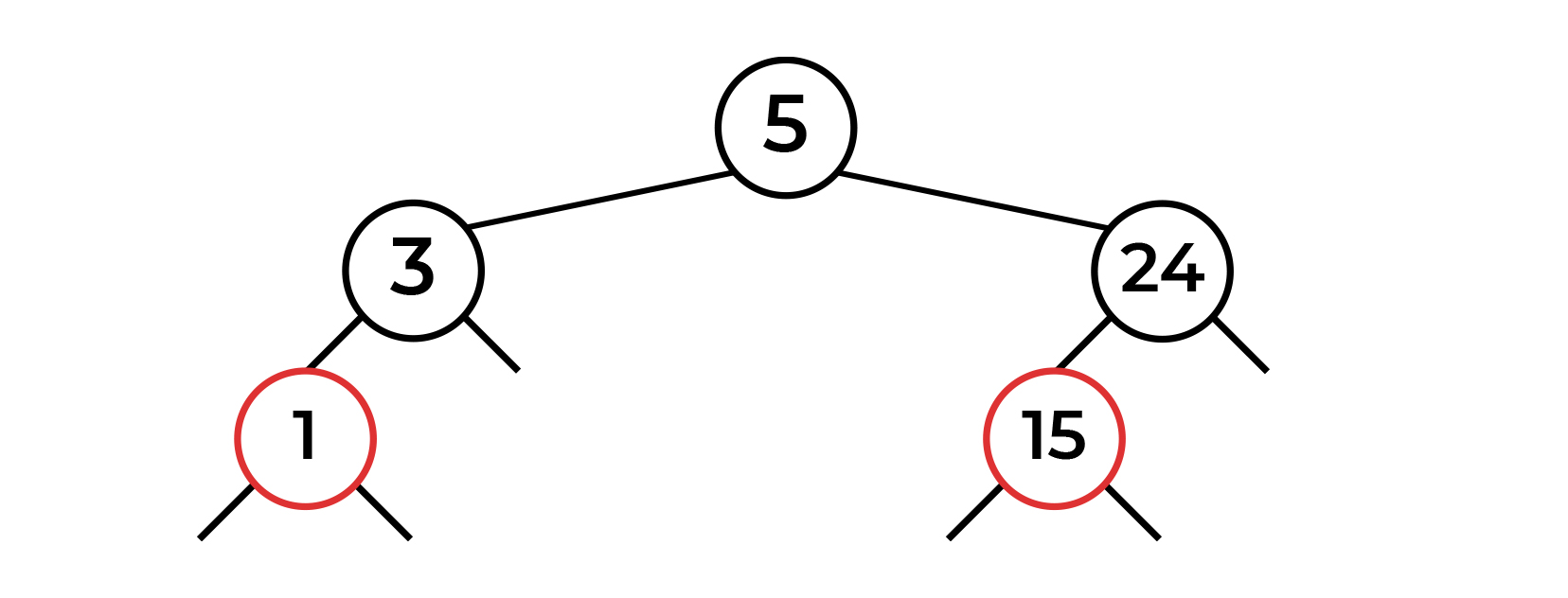
! .
, - , .
- 8. , . . , , .
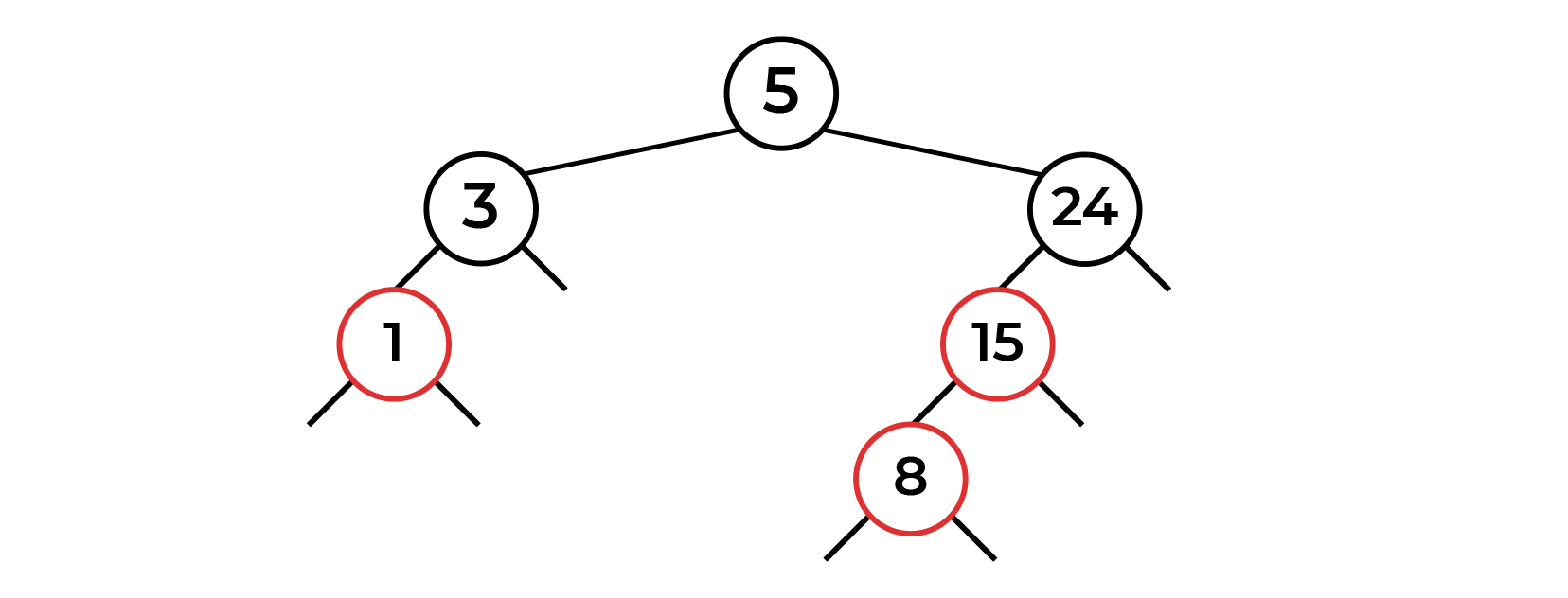
+ .
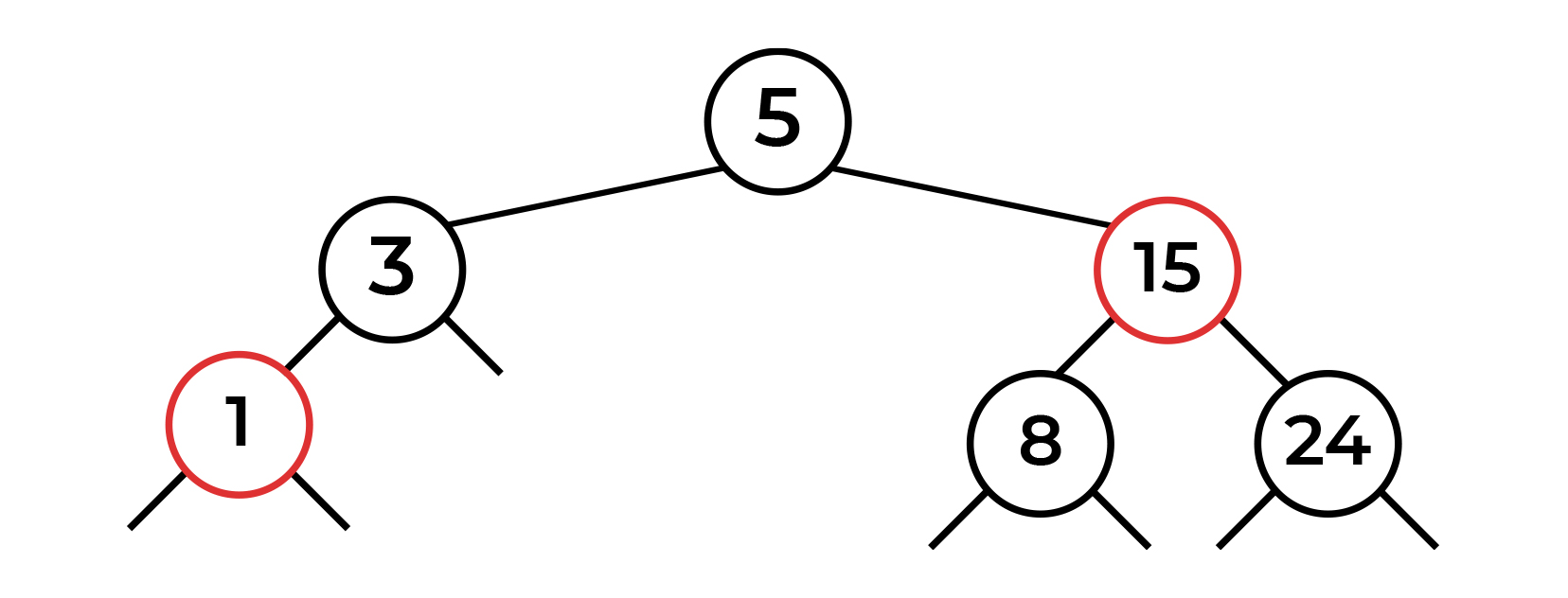
, ( 15) - , . . , - . . !
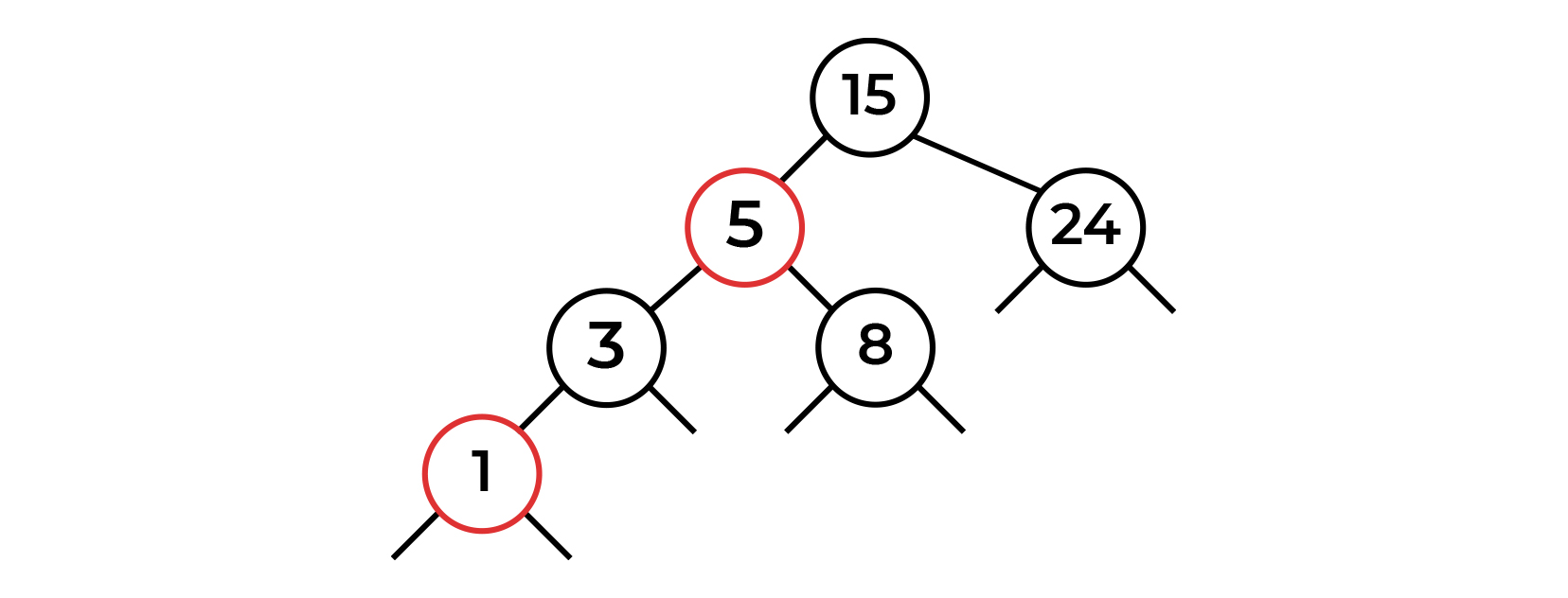
- - .
, . , , . . .
. , . 2-3 ( 13 16, , ).
- , , \. .
, , .
-
-
- - , . , , . , !
- , . , , . , !
Now you can go over the construction of the tree again and analyze, check the properties from the first article, ask the questions "what if ...?" (believe me, this is very useful!). In general, this is all I wanted to tell you about inserting a node into a left-side red-black tree.
A little about the value search operation
The operation of obtaining will be no different from searching in any other binary tree - the color is not involved in it in any way.
Conclusion
This concludes our second part about the insertion and balancing of the ccd. Ask your questions, criticize and supplement the article below! In the final, third, part I will talk about the most difficult topic of red-black tree - deleting an element. See you:)