🌗 👸🏾 🌦️ 6 reasons why you should avoid bar charts 👩🏾‍🌾 👎🏼 👩🏽‍🎤

Systematic errors are not alien to histograms. The fact is that they are rather arbitrary and can lead to incorrect conclusions about the data. If you want to visualize the variable, it is better to choose a different graph.

Whether you're in a meeting with senior management or data scientists, one thing you can be sure of is that a bar chart will appear at some point.

. : . , , ? .

— !

6 , , , :

«, : . ?» !

, CDP, .

, ?

1. .

, , (bins). ( ). ? , .

( ), 303 ( UCI : ).

( Python R), (). , . .

2. .

, , . , , . , .

, , .

How the histogram changes when the maximum value changes. [Author's drawing] — . [ ]

, . , : !

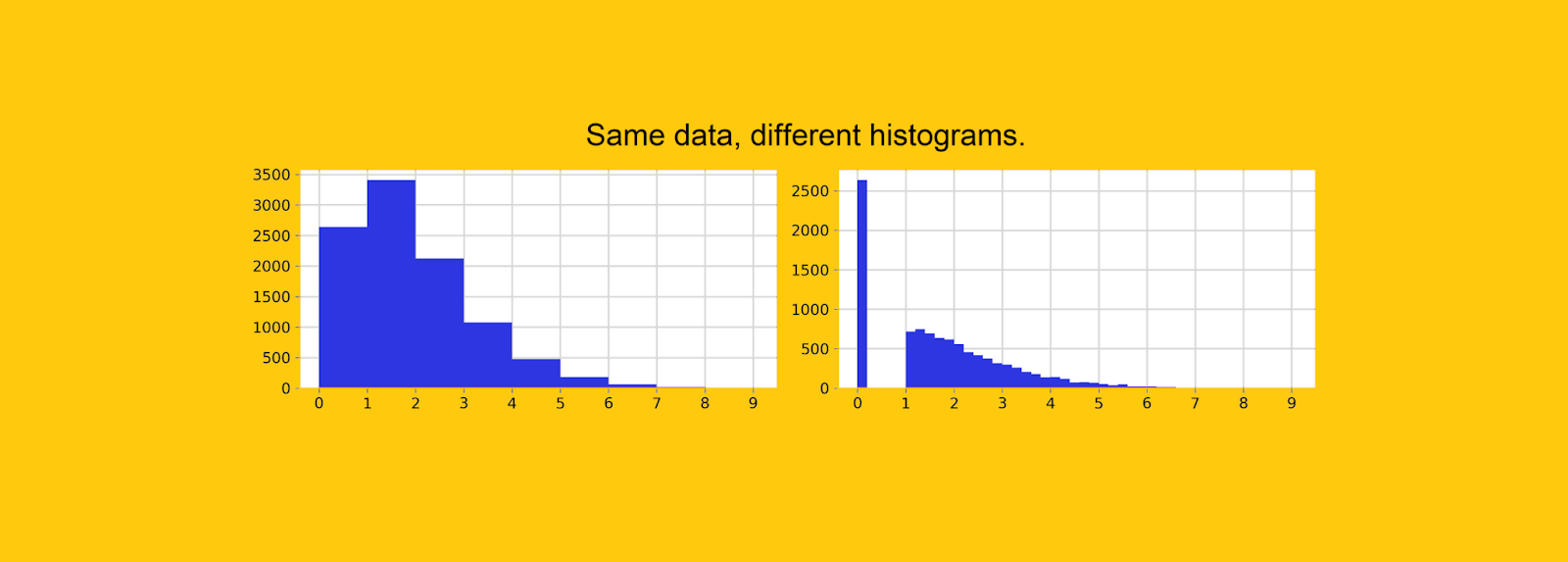
3. .

, , . , , «» .

, 0. , 10 , 26% — .

Same data, different bin width. It is impossible to find a high concentration of zeros in the left graph. [Author's drawing] — , . . [ ]

— , Python. , , , «» .

. , , , 0 - .

4. .

, . .

«» (Age). = 49 ( ) = 49,828884325804246 ( , 365,25). — , — .

On the left is a continuous variable. On the right is a discrete variable. However, they look the same in the top plots. [Author's drawing] — . . . [ ]

, , , , , . ( Python) : .

5. .

. , UCI , , :

60 .

Comparison of histograms. [Author's drawing] — . [ ]

, , , , .

6. , .

Excel, R Python, : Excel , R — hist(x), Python — plt.hist().

, . , , ? , , , , . :

| INTERVAL_LEFT | INTERVAL_RIGHT | COUNT |

|---------------|----------------|---------------|

| 75.0 | 87.0 | 31 |

| 87.0 | 99.0 | 52 |

| 99.0 | 111.0 | 76 |

| ... | ... | ... |

SQL- , . , Google Big Query :

WITH
STATS AS (
  SELECT 
    COUNT(*) AS N,
    APPROX_QUANTILES(VARIABLE_NAME, 4) AS QUARTILES
  FROM
    TABLE_NAME
),
BIN_WIDTH AS (
  SELECT
    -- freedman-diaconis formula for calculating the bin width
    (QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / ROUND((QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / (2 * (QUARTILES[OFFSET(3)] — QUARTILES[OFFSET(1)]) / POW(N, 1/3)) + .5) AS FD
  FROM 
    STATS
),
HIST AS (
  SELECT 
    FLOOR((TABLE_NAME.VARIABLE_NAME — STATS.QUARTILES[OFFSET(0)]) / BIN_WIDTH.FD) AS INTERVAL_ID,
    COUNT(*) AS COUNT
  FROM 
    TABLE_NAME,
    STATS,
    BIN_WIDTH
  GROUP BY 
    1
)
SELECT 
  STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * HIST.INTERVAL_ID AS INTERVAL_LEFT,
  STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * (HIST.INTERVAL_ID + 1) AS INTERVAL_RIGHT,
  HIST.COUNT
FROM 
  HIST, 
  STATS, 
  BIN_WIDTH

, ?

: .

6 , , : « ?» : , « » (Cumulative Distribution Plot - CDP). , , , .

— . , CDP :

x: ( );

y: .

— .

Graph of the cumulative distribution of the maximum heart rate. [Author's drawing] — . [ ]

x = 140 y = 90 (30%). : 140 . , 140 ( 90 , 30% ). , 30% 140 .

, , « » ? «»? . , ( , ). , CDP , , .

CDP . , , « 140 160?» « 180?». CDP, . .

CDP , . , :

1. . , CDP.

2. . CDP, .

3. . - , , , .

4. . (.. ), , .

5. . , , . , y 0 100%, . , , :

Comparison of distributions in CDP. [Author's drawing] — CDP. [ ]

6. , . , , , SQL:

SELECT 
  COUNT(*) AS N,
  APPROX_QUANTILES(VARIABLE_NAME, 100) AS PERCENTILES
FROM
  TABLE_NAME

Excel, R, Python

Excel . 101 , 0 1. , : =PERCENTILE(DATA, FRAC), DATA - , , FRAC - : 0,00, 0,01, 0,02, 0,03,…, 0,98, 0,99, 1. , x.

R :

plot(ecdf(data))

Python:

from statsmodels.distributions.empirical_distribution import ECDF
import matplotlib.pyplot as plt
ecdf = ECDF(data)
plt.plot(ecdf.x, ecdf.y)

! , .

. , Linkedin.

- "Machine Learning. Basic". , .

- "Machine Learning. Basic"

- - " "

6 reasons why you should avoid bar charts

, ?