See the previous post here .
Testing statistical hypotheses
For statisticians and data scientists, testing a statistical hypothesis is a formal procedure. The standard approach to testing a statistical hypothesis involves defining the field of study, deciding which variables are needed to measure the subject matter, and then proposing two competing hypotheses. To avoid considering only those data that support our subjective assessments, researchers clearly state their hypothesis in advance. Then, based on the data, they apply sample statistics to confirm or reject this hypothesis.
Statistical hypothesis testing involves the use of test statistics, i.e. sample value as a function of observation results. A test statistic is a value calculated from sample data that is used to assess the strength of data confirming a null statistical hypothesis and is used to identify a measure of discrepancy between empirical and hypothetical values. Specific verification methods are called tests, for example, z-test, t-test (respectively, Fisher's z-test, Student's t-test), etc. depending on the test statistics used in them.
Note . In domestic statistical science, the "vague" term "criterion statistics" is used. Foggy because here we again observe a soft substitution: instead of a test, a criterion arises. For that matter, a criterion is a principle or a rule. For example, when doing z-test, t-test, etc., we use z-statistic, t-statistic, etc. accordingly. in the rule for rejecting the hypothesis. This is nicely summarized by the following table:
Testing the hypothesis |
Test statistics |
Hypothesis rejection rule |
z-tests |
z-statistics |
If the test statistic ≥ z or ≤ -z, then reject the null hypothesis H 0 . |
t-tests |
t-statistics |
If the test statistic is ≥ t or ≤ -t, then reject the null hypothesis H 0 . |
Analysis of variance (ANOVA) |
F-statistics |
≥ F, H0. |
- |
- |
≥ χ, H0. |
, -, - . , , -.
, « - »? . , . , , . , , . H0.
, , , , . « » , , -, , , .
, H1. , . , , . , - , :
H0: - -
H1: - -
, - -. «» (.. ), , , . (.. , ), .
, , .
, . , , , .
, :
,
,
, 1- 2- :
|
H0 |
H0 |
H0 |
|
1- ( ) |
H0 |
2- ( ) |
|
1- , 2- . , , , , . , , .
. 5% 1%. 5% , 1% — . α () . , ( -, ), , . , , . 5%, .
-
- AcmeContent , -, . , , - .
, , AcmeContent - . - , 5% -. . . , , "0", ( , ) , "1".
z-
, .
z- . , -, , , .
, . Z- , .. (), . , , , :
σ2a — a, σ2b — b na nb — a b. Python :
def pooled_standard_error(a, b, unbias=False):
''' '''
std1 = a.std(ddof=0) if unbias==False else a.std()
std2 = b.std(ddof=0) if unbias==False else b.std()
x = std1 ** 2 / a.count()
y = std2 ** 2 / b.count()
return sp.sqrt(x + y)
, , . z:
pooled_standard_error
, , z- :
def z_stat(a, b, unbias=False):
return (a.mean() - b.mean()) / pooled_standard_error(a, b, unbias)
z , , . , z- , . , , z- :
def z_test(a, b):
return stats.norm.cdf([ z_stat(a, b) ])
z- -. -, , - . groupby('site')['dwell-time']
. get_group
, -:
def ex_2_14():
'''
- z-'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
print('a n: ', a.count())
print('b n: ', b.count())
print('z-:', z_stat(a, b))
print('p-: ', z_test(a, b))
a n: 284
b n: 16
z-: -1.6467438180091214
p-: [0.04980536]
5% 95%. , , 95%- . , , 5%- .
P- — 1- , . p-, , , .
0.0498, 4.98%. 5% , , .
:
H0: - -
H1: - -.
, - .
, - -, — , , . , - 16 . , .
, , .
t-
t- , , , .
1908 , , , . «».
— , t- , . , t- , 1. , , .
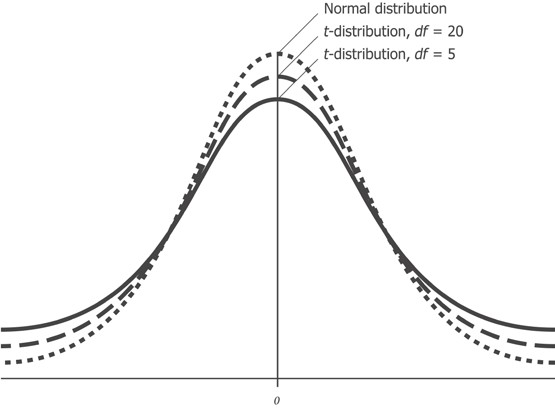
, t- . .
, df . degrees of freedom, . , .
, , , 10 8, , , 12. , , , , .
, , , 10, 10, . , 10, 10, , , .
: , . : .
, .
t-
t- t-. z-, . t- t- :
Sa̅b̅ — . , :
σa σb, . t- ().
, t- :
. , t- . :
def pooled_standard_error_t(a, b):
''' t-'''
return sp.sqrt(standard_error(a) ** 2 +
standard_error(b) ** 2)
t- z- -, :
t_stat = z_stat
def ex_2_15():
''' t-
-'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_stat(a, b)
-1.6467438180091214
, — z- , .
t-
t- , p-. t-, t-, :
def t_test(a, b):
df = len(a) + len(b) - 2
return stats.t.sf([ abs(t_stat(a, b)) ], df)
, 298.

, . :
H0:
H1:
:
def ex_2_16():
'''
- t-'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test(a, b)
array([ 0.05033241])
p-, 0.05. α, 5%, , . t- . , z- .
, - . , .
, , , , . «» , α . , , , , .
— . , .
, 1- . , - . α , -.

stats scipy t-. stats.ttest_ind
. - . equal_var
True
, , , ( t_test_verbose
, ( ):
def ex_2_17():
''' t-'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(1)
return t_test_verbose(a, sample2=b, fn=stats.ttest_ind) #t-
{'p-': 0.12756432502462475,
' ': 17.761382349686098,
' ': (76.00263198799597, 99.89877646270826),
'n1 ': 284,
'n2 ': 16,
' x ': 87.95070422535211,
' y ': 122.0,
' x ': 10463.941024237296,
' y ': 6669.866666666667,
't-': -1.5985205593851322}
t- t_test_verbose
p-. P- 2 , . , , , , stats t-, t- , , . , , .
t-
t- , , . , , , sciy stats.ttest_1samp
.
. , , - , 90 ., :
def ex_2_18():
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
return t_test_verbose(b, mean=90, fn=stats.ttest_1samp)
{'p- ': 0.13789520958229415,
' df ': 15.0,
' ': (78.4815276659039, 165.5184723340961),
'n1 ': 16,
' x ': 122.0,
' x ': 6669.866666666667,
't- ': 1.5672973291495713}
t_test_verbose
p- , . 78.5 165.5 ., , , 90 . . , .
, t- , , , . resampling. , . , , , , , .
, — . , , , , . , . . , .
, , — , ( ) , « », ( , , .).
pandas sample . , .. n
( , ), axis
(, ) replace
( ), False
. , :
def ex_2_19():
'''
'''
groups = load_data('new-site.tsv').groupby('site')['dwell-time']
b = groups.get_group(1)
xs = [b.sample(len(b), replace=True).mean() for _ in range(1000)]
pd.Series(xs).hist(bins=20)
plt.xlabel(' , .')
plt.ylabel('')
plt.show()
:

, , -. , 16 , ( 78 165 .), t-.
, , . , , .
-. , , .
, - AcmeContent -. , 19 . -, , 20 -, .
- 19 - . , 5% , 24 .
, -. , 0 - , 1 19 :
def ex_2_20():
df = load_data('multiple-sites.tsv')
return df.groupby('site').aggregate(sp.mean)
:
site |
dwell-time |
0 |
79.851064 |
1 |
106.000000 |
2 |
88.229167 |
3 |
97.479167 |
4 |
94.333333 |
5 |
102.333333 |
6 |
144.192982 |
7 |
123.367347 |
8 |
94.346939 |
9 |
89.820000 |
10 |
129.952381 |
11 |
96.982143 |
12 |
80.950820 |
13 |
90.737705 |
14 |
74.764706 |
15 |
119.347826 |
16 |
86.744186 |
17 |
77.891304 |
18 |
94.814815 |
19 |
89.280702 |
-, , - . - , Python itertools, , :
import itertools
def ex_2_21():
''' - t-
" "'''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
pairs = [list(x) # n k
for x in itertools.combinations(range(len(groups)), 2)]
for pair in pairs:
gr, gr2 = groups.get_group( pair[0] ), groups.get_group( pair[1] )
site_a, site_b = pair[0], pair[1]
a, b = gr['dwell-time'], gr2['dwell-time']
p_val = stats.ttest_ind(a, b, equal_var = False).pvalue
if p_val < alpha:
print(' - %i %i : %f'
% (site_a, site_b, p_val))
. , , , . , , - .
, - — , 90 ., -:
def ex_2_22():
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group( site_a )['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print(' %i - : %f'
% (site_a, p_val))
-, :
6 - : 0.005534
10 - 10 : 0.006881
p- ( 1%) , . , . t- 20 α, 0.05. α , . 20- t- , - 20.
, t- . . .
, . — , , 1- . .
— α . , k -, α 0.05, :
1- . ex-2-22
, , α :
def ex_2_23():
''' - t-
(0) '''
groups = load_data('multiple-sites.tsv').groupby('site')
alpha = 0.05 / len(groups)
baseline = groups.get_group(0)['dwell-time']
for site_a in range(1, len(groups)):
a = groups.get_group(site_a)['dwell-time']
p_val = stats.ttest_ind(a, baseline, equal_var = False).pvalue
if p_val < alpha:
print(' %i - : %f'
% (site_a, p_val))
, , - .
— 1- , 2- . , , - .
, №4, , 1- 2- , 20 - .