I. Foreword
It all started with the fact that on January 26, 2021, in my classmates, I received a message from Valery Ivanov:
Vladimir, in VA them. Dzerzhinsky, when did you study and in which group?
I wrote to Valery:
1971-1976 Department 25, NK-25 - Zakharov V.N., head of the course - kennel Grigoriev, coursework - Kuznetsov Yu.M. 1979-1982 postgraduate studies of the 25th department
And from him came the answer:
Volodya, I am Ivanov Valery Petrovich, conscript, 23rd group ...Yes, I remembered him. He was the only conscript on our course at the Military Academy. F.E. Dzerzhinsky (abbreviated VAD).
In those years, the Academy. F.E. Dzerzhinsky was located in the capital of our Motherland, Hero City Moscow, on the embankment of the Moskva River in Kitay Gorod :
Between the academy and Red Square during the years of our studies there was a hotel Russia, on the site of which today stands the Zaryadye Park. The last time I was at the Academy in Kitaygorodsky passage in 2002:
But the Military Academy. F.E. Dzerzhinsky ceased to exist even earlier. By the decree of the President of the Russian Federation dated August 25, 1997, the academy, in order to revive the historical traditions of the Russian armed forces and taking into account the exceptional merits of Peter I in creating a regular army, was renamed the Peter the Great Military Academy of the Strategic Rocket Forces:
Unfortunately, in 2015, "Dzerzhinka ", As it is called in the old fashioned way, has moved from the center of Moscow to Balashikha near Moscow.
But I digress a little. Two weeks later, a new message came from Valery Ivanov:
Volodya, we were taught well. I was solving important and interesting problems in uniform. After his dismissal, he participated in the creation of a facility for the treatment of malignant tumors with a vortex magnetic field. Our installation treats people in the Krasnodar Diagnostic Center, in the Krasnodar Medical Academy, in Novorossiysk, in Armavir, ... I also worked in laser technology, for radio systems ... As part of another organization I participated in a tender for the development of an information security system in the interests of the Ministry of Internal Affairs of Russia ... I have his view on the problem of information security, developed his theory at the level of modern vision from the standpoint of the modern era of science.
...
, , . . . .
…
. , . … : , . , ...:
To say that we were taught well is to say nothing. They taught us at the highest level!
I was intrigued by his words "my mathematical assessment of the security of information when using cryptographic means of protecting information in the extreme case . "
A month later, he sent me an article with the following title:
TO THE TWENTY-FIVE YEARS OF THE CREATION OF THE ALGORITHM OF CRYPTOGRAPHIC PROTECTION OF INFORMATION GOST 28147-89
After reading the article (especially without going into its title, namely the twenty-fifth anniversary ), I answered him:
, 24 2021 . 16:50:19 MSK :
> — >
, ! !
.
:
, 28147-89.
— . .
, 28147-89 Magma Kuznyechik ( ).
28147-89.
28147-89 34.10-2001 34.11-94 .
. . , .
And only after sending this letter, I realized that the article was written 7 (seven) years ago and the anniversary was already in 2014. On the other hand, the approach itself is very beautiful, from my point of view, and it can be applied to Magma and Grasshopper. And I decided to once again clarify the position of the author on the publication of the article on Habré. And the author replied:
Valery Ivanov
April 5 at 21:37
Volodya, I trust you….
Volodya, at your discretion!….
After that, I finally decided to write this material.
Below is an article by Valery Ivanov (pictured on the right) without cuts.
II. Original article
| GOST 28147-89 is dedicated to the creators of the cryptographic information protection algorithm. |
TO THE TWENTY-FIVE YEARS OF THE CREATION OF THE ALGORITHM OF CRYPTOGRAPHIC PROTECTION OF INFORMATION GOST 28147-89
INTRODUCTION
The guidelines of the FSTEC of Russia require the use of an algorithm for cryptographic protection of information defined by GOST 28147-89 in information security systems. This year marks twenty-five years since the beginning of the operation of this algorithm; it has passed from the second to the third millennium. This time was accompanied by an increase in the computing power of computer technology, which can be attracted by a malicious party. Because of this, the task of assessing the prospects for using this algorithm from the perspective of the third millennium is urgent.
The purpose of this article is to assess the prospects of this algorithm by introducing modern concepts of physics into consideration by introducing an abstract computer with extreme technical characteristics.
1. Mathematical model for assessing the security of information with a cryptographic algorithm GOST 28147-89
In our case, there is a process of interaction between objects - carriers of fundamental concepts:
- information to be protected (encrypted by intruders);
- the environment for the existence of information, includes:
- object - malefactors, decrypt the intercepted message;
- object - a message encrypted in accordance with GOST 28147-89, which forced the attackers to decrypt the text by brute-forcing the keys, is determined by the number of operations to brute-force all the keys.
- time is like a clock.
Let the attackers be able to use the highest performance computing facilities that are possible in the conditions of planet Earth.
Investigation of the process of interaction of these objects makes it possible to detect the following chain with a finite set of states:
S 0 - a state when the information to be protected during the period when it retained its value could not be deciphered (negative result for attackers).
S 1 - the state of decryption of the information to be protected.
S 2- the state when the attackers managed to decrypt the intercepted information during the period of time when it retained its value (positive result for).
Let the information aging time be characterized by its aging distribution function B (t) with aging intensity - β .
The transition from state S 1 to state S 2 is determined by the intensity of the decryption information to be protected is determined by decoding the information distribution function - S (t) with the decryption intensity - S .
Then the interval time of aging of intercepted information in a certain time interval maintains the value is:
.
Then, in cases of exponential distribution of both the aging time of the information intercepted by the attacker and the decryption time of the intercepted information, the probability that the attackers will not be able to decrypt the information to be protected until the information loses value will be determined by the following mathematical expression:
The numerical value of the aging time parameter β determines the owner of the information, and the decryption parameter S determines the performance of the computing facilities that the attacker was able to attract.
Let's move on to examining a computing tool that an attacker can attract.
2. Assessment of information security by cryptographic means of information security GOST 28147-89
Let us introduce into consideration a certain structured material formation - an abstract computer considered by M. H. Bremmermann [1,4]. To solve the problem of decrypting a text intercepted by an intruder, the computer must process N bits. By "processing N bits" we mean the transfer of N bits through one or more channels of the considered computing system.
Obviously, in order to work, information must be physically encoded in a certain way. Suppose that it is encoded in the form of energy levels of a certain type of energy in the interval [0, E] , where E is the amount of energy that we have for this purpose. Let us further assume that the energy levels are measured with an accuracy of ∆E .
In this case, the entire interval can be divided by the maximum into N = E / ∆E equal sub- intervals , and each of them will correspond to an energy equal to ∆E .
In the case when no more than one level is always occupied, then the maximum number of bits represented by the energy E will be equal.
In order to represent a large amount of information with the same amount of energy, it is necessary to reduce ∆E . This is possible only up to a certain limit, since it is necessary to distinguish the obtained levels using a certain measuring procedure, which, regardless of its essence, always has limited accuracy. The maximum accuracy is determined by the Heisenberg uncertainty principle, known from the physics course: energy can be measured with an accuracy of ∆E if the inequality is satisfied
where: ∆tIs the duration of the measurement time, h = 6.625x10 -27 erg / s is Planck's constant, and ∆ is determined as the average deviation from the expected energy value.
This means that the number of bits that an abstract computer can process in the time interval ∆t will be:
Let us now represent the available energy E by the corresponding amount of mass. Then, according to Einstein's formula, we get
where: c = 3x10 10 cm / s - the speed of light in vacuum.
Thus, the upper, most optimistic bound for the number of bits is N , which may treat SVT any nature mass m in the time interval can be found from the expression:
Substituting the values for a and h and mass m = 1 g , the time interval equal to 1 , we abstract information processing speed of computer mass of 1 g :
From Hans Bremmermann concluded: There is no data processing system, artificial or natural, that can process more than 2x10 47 bits per second per gram of its mass.... This numerical value can be considered as the speed of an abstract computing system weighing 1 g.
In our case, by a bit we mean a decrypted text of a certain length plus an assumed key on which the intercepted text is encrypted. And under the processing of one bit - the operation of decrypting the intercepted text using the assumed key, deciding on the results of decryption and choosing the next key. It is obvious that we have placed the attacker in extremely comfortable conditions.
It is known that the strength of a cryptographic protection algorithm is determined by the number of operations Q required to enumerate keys. For the considered algorithm Q = 10 70 .
Then the average search time of all keys for an abstract computer with mass m will be:
and the decryption rate:
For decryption and aging functions, distributed according to exponential law, the probability that the information to be protected will be decrypted after the moment when the information loses its value (after information aging) will be determined in accordance with the theory of catastrophes, as:
Let the aging time of the information intercepted by the intruder be defined as 30 years, then, provided that the year is 3.14x10 7 seconds, the aging rate of the intercepted information will be:
Let it be required to ensure the probability of excluding decryption of the text to be protected during the aging time equal to 30 years with the probability P = 0.9999.
Then the mass of the computing system that ensures compliance with the specified requirement can be determined from the expression
Substitute the calculated values of β into it, as well as the known value of Q, we obtain the boundary value of the mass of the abstract computer, below which the specified value of the encrypted information security is provided.
In our case
tons, which is a value that is "unbearable" not only at the present time, but also in the distant future, since today the most powerful super-computer operated on Earth has a performance of about 1000 teraflops, its performance is significantly inferior to the performance of a computing system weighing 1 g highly organized matter according to Bremmermann.
It follows that the algorithm for cryptographic protection of information GOST 28147-89 recommended by the FSTEC of Russia, built on the basis of a key length of 256 bits, provides the required level of security of the information to be protected.
Under the same conditions, the requirements for the strength of the encryption algorithm were determined for the case when the malicious party has a computer equal to the mass of the planet Earth:
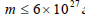... It was determined that the key length in this case should be at least 293 bits.
Conclusion
The author does not know the cases of breaking the considered algorithm, from which he believes that the above allows us to conclude that at present a very reliable algorithm for cryptographic protection of information GOST 28147-89 is being used, based on a key whose length provides the necessary strength. The author also believes that this algorithm is destined for a long and worthy fate in the third millennium, and its creators deserve great respect and gratitude from their descendants.
Literature
- J. Clear. Systemology. Automation of solving system problems. M. Radio and communication. 1990 year
- V.P. Ivanov. On the foundations of the theory of information security as an internally perfect and externally justified scientific theory. Special equipment No. 3-4, 2008
- I. G. Ivanov, P. A. Kuznetsov, V.I. Popov. Methodological foundations of information protection in automated banking complexes. In the journal Confident No. 1, 1994
- Bremmermann, H, J. Optimization through evolution and recombination. In: Self - Organizing Systems, edited by MS Vovits and S. Cameron, Spartan, Washington. DC, 1962, pp 93-106.
III. Afterword
It should be noted that V. Ivanov did not stop there. Here is a quote from another of his letters:
, … . . . . , . , , , ( 30 , , - ). . , , , ! ! , ...
And V. Ivanov wrote a very interesting article "On the foundations of information protection as a scientific field in the modern era of science." But this is a topic for another conversation.