This article will focus on such concepts of number theory as the digital root and the Vedic square.
This article does not say anything about numerology, except that it is a pseudoscientific concept.
The purpose of this article: to show the mathematical patterns around calculating the digital root and its relationship with cyclic numbers.
Introduction
A few days ago I decided to write a simple article about numerological addition. My goal was to show that even such a simple operation can have a large number of interesting patterns. I found many of these patterns back in school, when I was bored in geography lessons. Upon closer inspection, I found more patterns than I expected, and this led me back to my favorite full reptend prime theme .
After that, I carefully studied what I found, learned that many of these concepts already exist, and decided to rewrite the article again in order to rely on well-known concepts. In addition to the well-known concepts, I have added my own visualizations to make reading a little more fun.
Sum of digits and digital root
The digital root of a natural number in a given number system is the value obtained by iteratively calculating the sum of digits , where at the first iteration, the sum of the digits of a natural number is calculated, and at each next iteration, the sum of the digits of the result of the previous iteration is calculated. The operation is performed until the calculated value becomes less than the specified number system, i.e. until it equals a single digit.
The additive strength of a natural number is the number of iterations at which it is necessary to apply the operation of the sum of digits in order to obtain the digital root.
Example: The digital sum of 142857 is 1 + 4 + 2 + 8 + 5 + 7 = 27
The digital sum of 27 is 2 + 7 = 9
As a result, the digital root of the number 142857 = 9, the additive durability 142857 = 2.
Python:
def digitalRootRecurrent(number, base):
digitSum = 0
while number > 0:
digitSum += number % base
number //= base
if digitSum >= base:
digitSum = digitalRootRecurrent(digitSum, base)
return digitSum
: , - 1, - 1.
:
def digitalRoot(number, base):
if number == 0:
return 0
dR = number % (base - 1)
if dR == 0:
dR = base - 1
return dR
, , :

:
firstTermRangeStart = 2
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print()
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
if i % (secondTermRangeEnd + 1) == 0:
print()
print('dr(',j,'+', i, ') =', digitalRoot(j + i, base), ' ', end='')
, :
, .
: 455 - 123 = 332.
, 4 - 6 8, , :
, :

:
firstTermRangeStart = 1
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
print()
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print('dr(',j,'*', i, ') =', digitalRoot(i * j, base), ' ', end='')
:
1) [1, 2, 3, 4, 5, 6, 7, 8, 9]
2) [2, 4, 6, 8, 1, 3, 5, 7, 9]
3) [3, 6, 9, 3, 6, 9, 3, 6, 9]
4) [4, 8, 3, 7, 2, 6, 1, 5, 9]
5) [5, 1, 6, 2, 7, 3, 8, 4, 9]
6) [6, 3, 9, 6, 3, 9, 6, 3, 9]
7) [7, 5, 3, 1, 8, 6, 4, 2, 9]
8) [8, 7, 6, 5, 4, 3, 2, 1, 9]
9) [9, 9, 9, 9, 9, 9, 9, 9, 9]
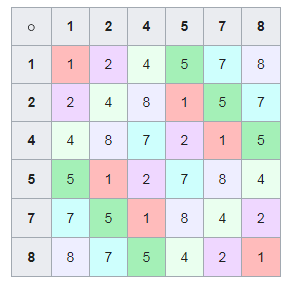
, 1 8, 2 7, 3 6, 4 5. , , , , - 1.
, -1 - 1. 1 .
:
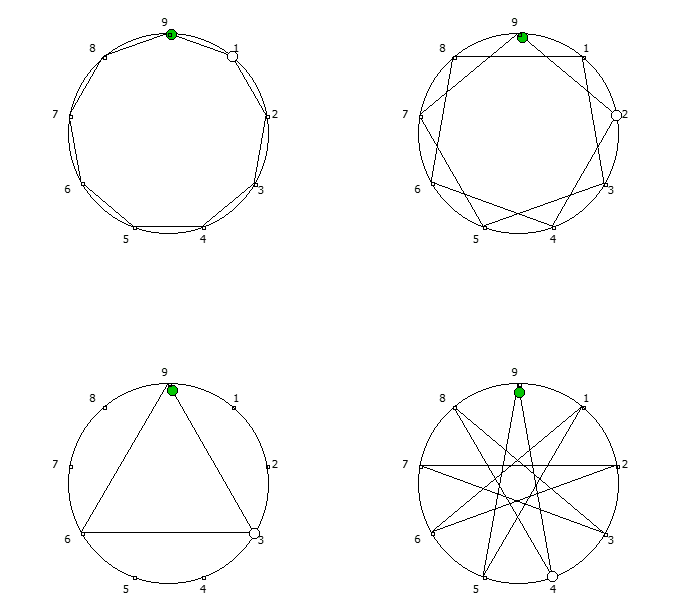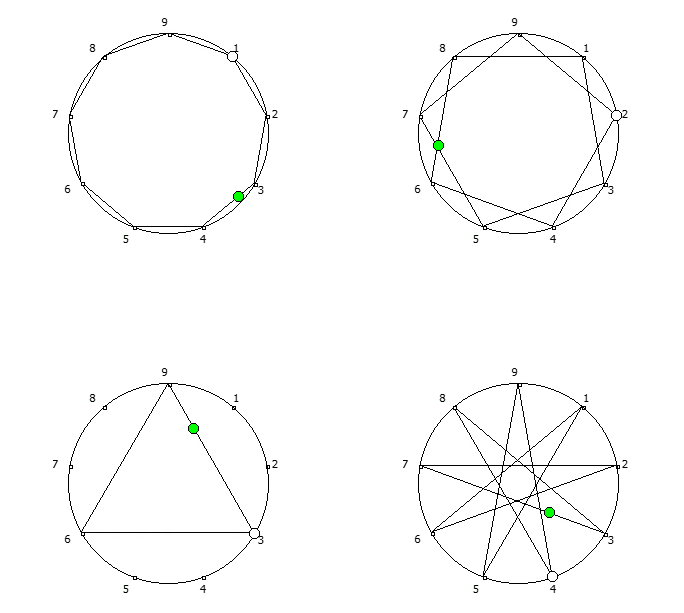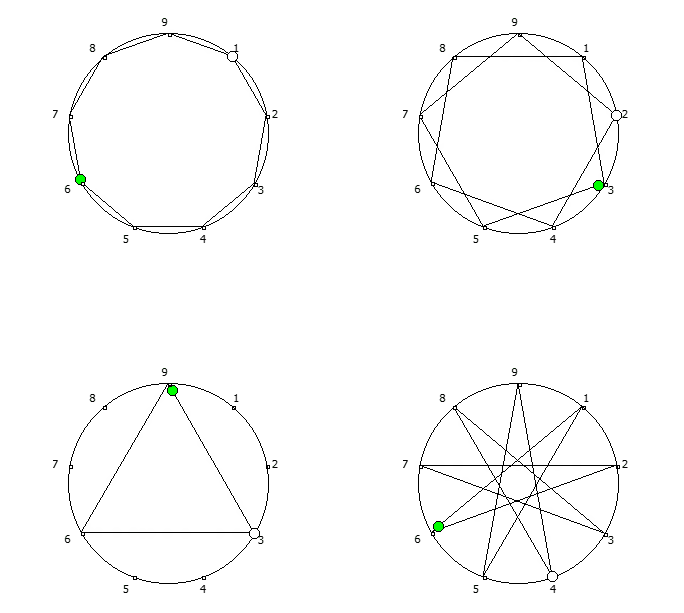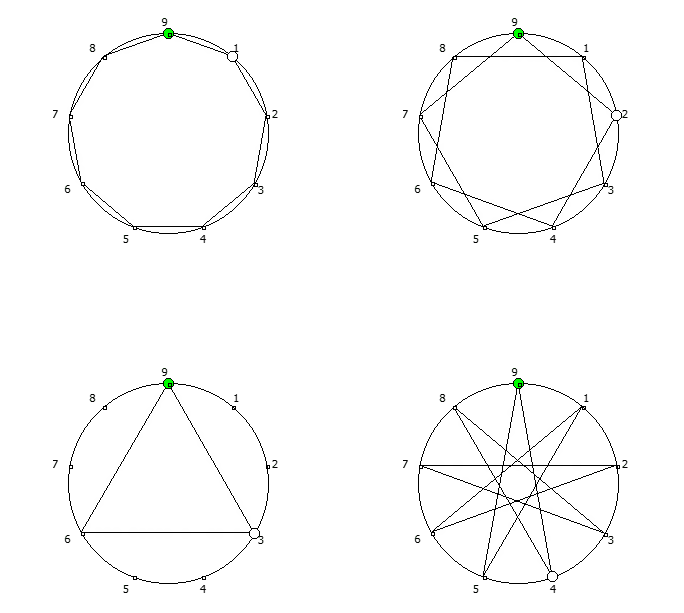
, - 1, n-. , - 1, 3 6.
:
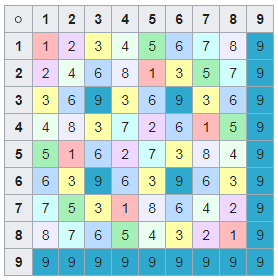

:
, . , , .
100 1000. - - 1, - , 1.

. .
, , , .
, , 2, 5, 4, 8.
, , 1000; 1000 1, .

base = 10
divisors = [2, 4, 5, 8]
for j in divisors:
print()
for i in range(1, base):
value = (digitalRoot(int((i / j) * (base ** 3)), base))
print('dr(',i, '/', j, ') =', value, ' ', end='')
. 9 , , 9. 3 6, , .
:
2) [5, 1, 6, 2, 7, 3, 8, 4, 9] - 5
4) [7, 5, 3, 1, 8, 6, 4, 2, 9] - 7
5) [2, 4, 6, 8, 1, 3, 5, 7, 9] - 2
8) [8, 7, 6, 5, 4, 3, 2, 1, 9] - 8
, .
:

base = 10
.
for i in range(2, base - 2):
print()
for j in range(1, base - 1):
print('dr(', j ,'^', i, ') =', digitalRoot(i ** j, base), ' ', end='')
.
, , - full reptend prime.
, . , : , p^n + 1, p — , n - .
8, [1, 3, 2, 6, 4, 5]. .
![1 7 . [1, 3, 2, 6, 4, 5]. 1 7 . [1, 3, 2, 6, 4, 5].](https://habrastorage.org/getpro/habr/upload_files/740/9dc/7d8/7409dc7d835e4080385e4973454b939c.png)
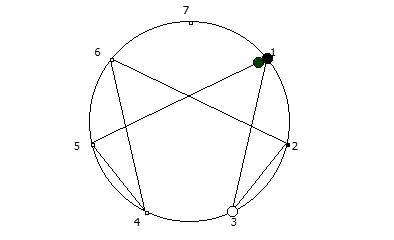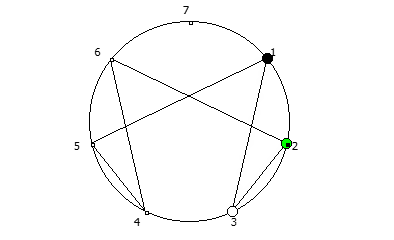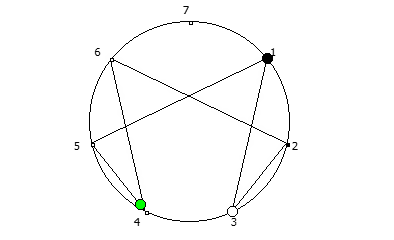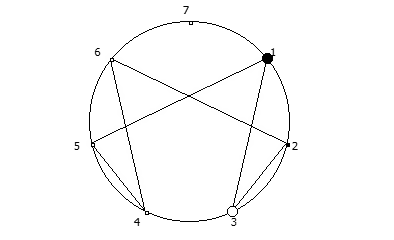
, :
, , 1/P, P - full reptend prime.
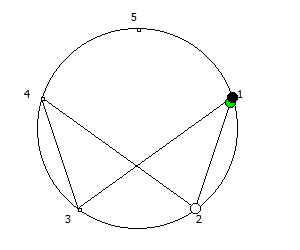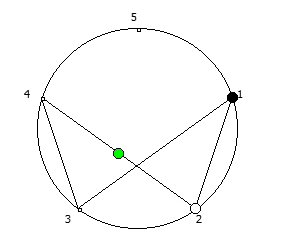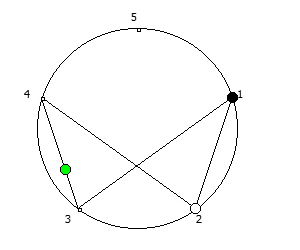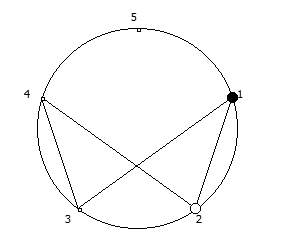
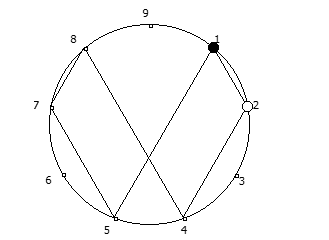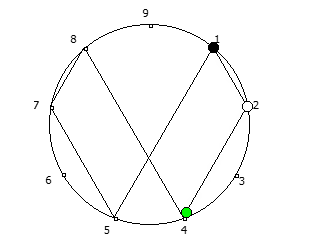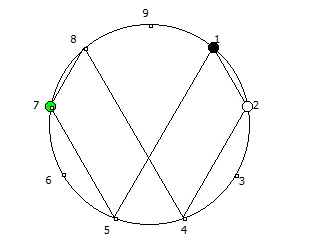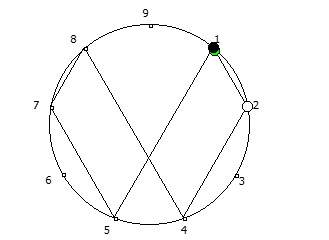

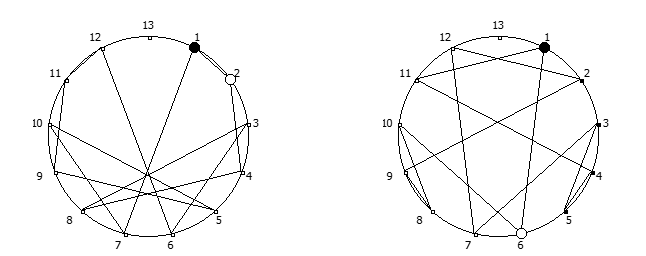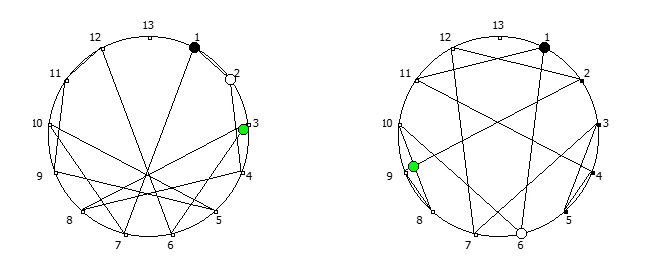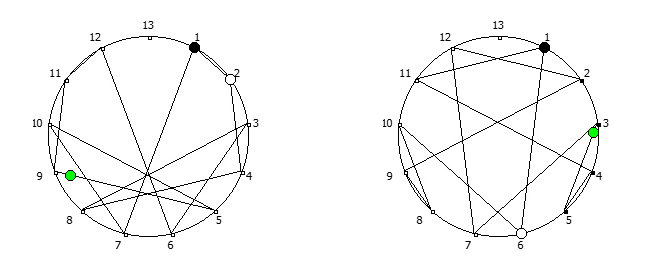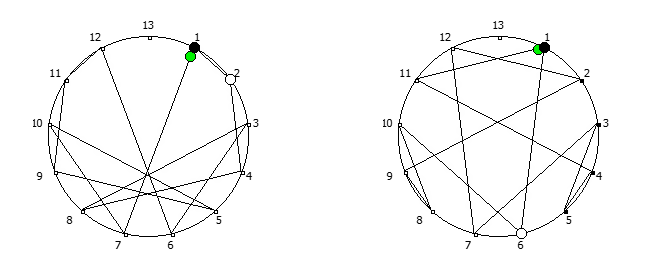
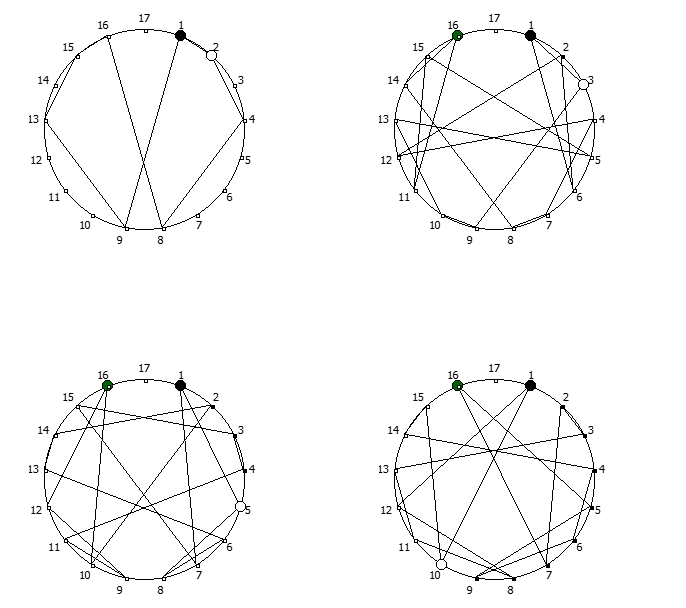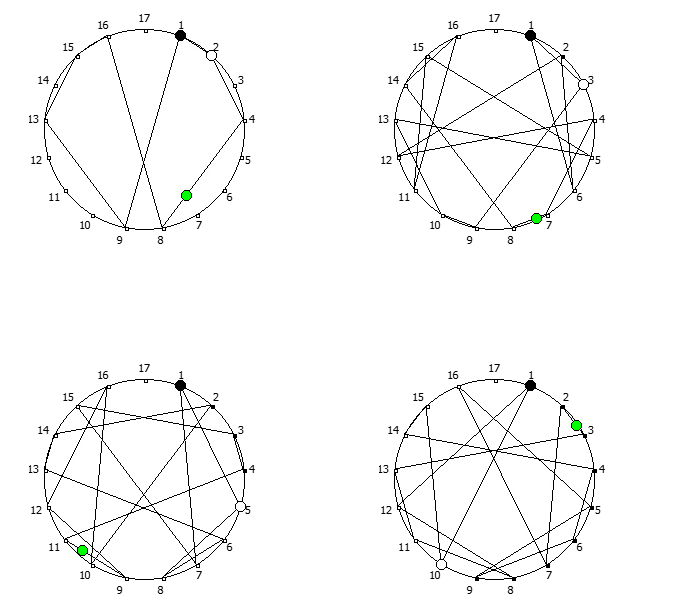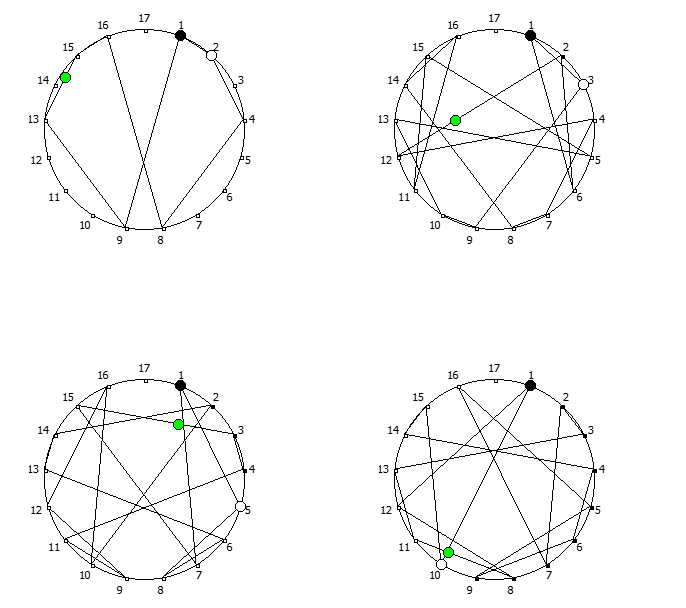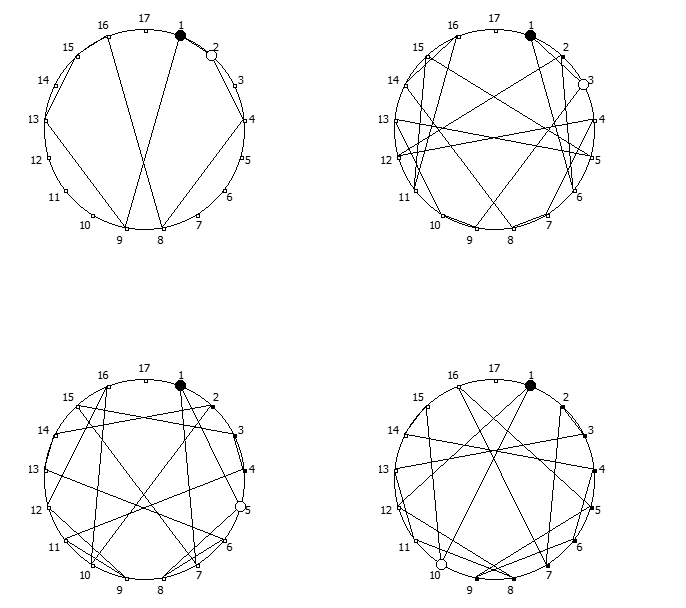

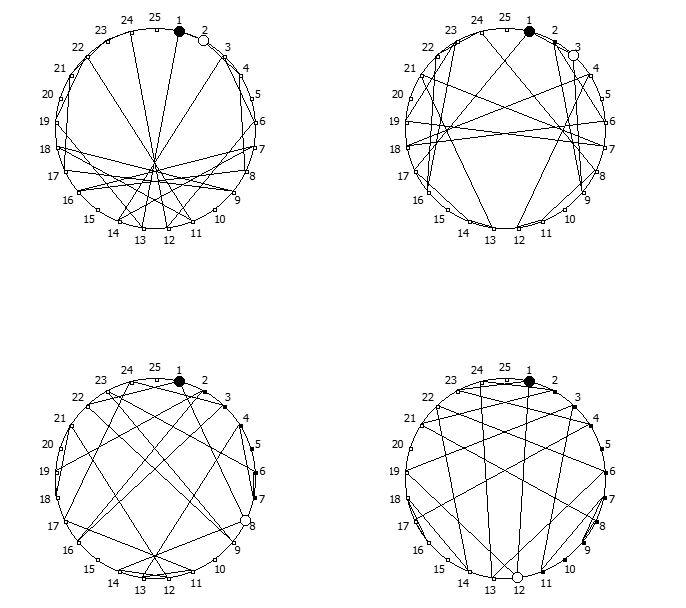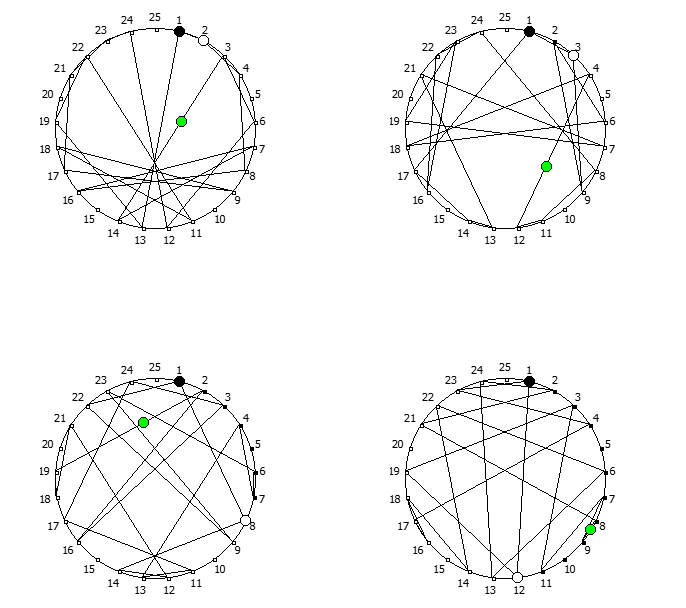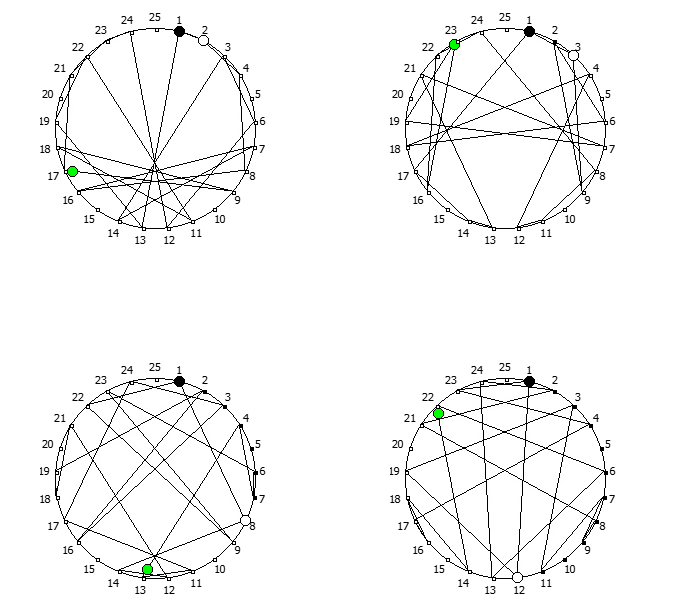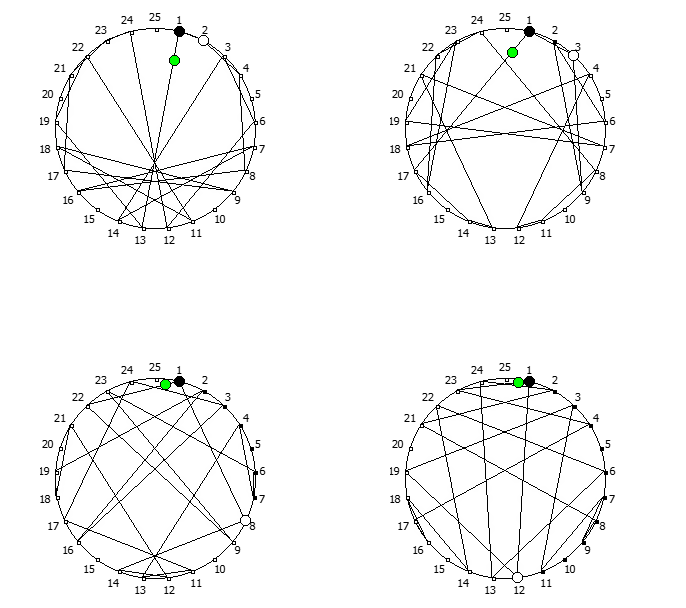

, , :
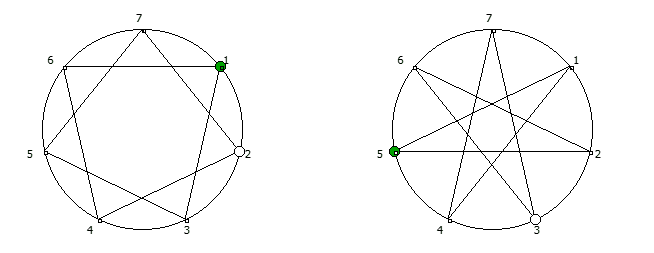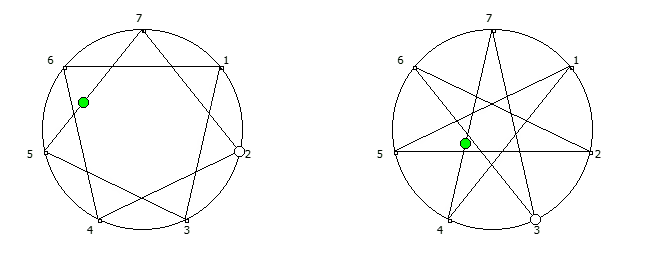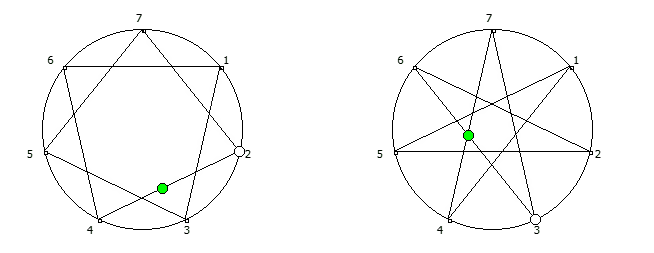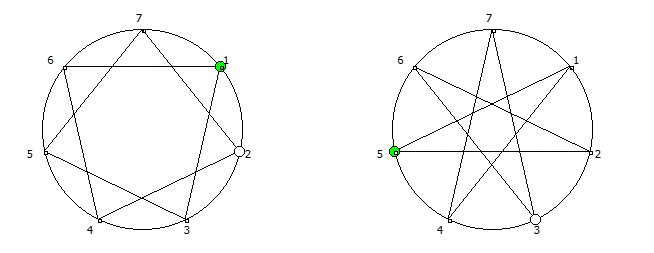
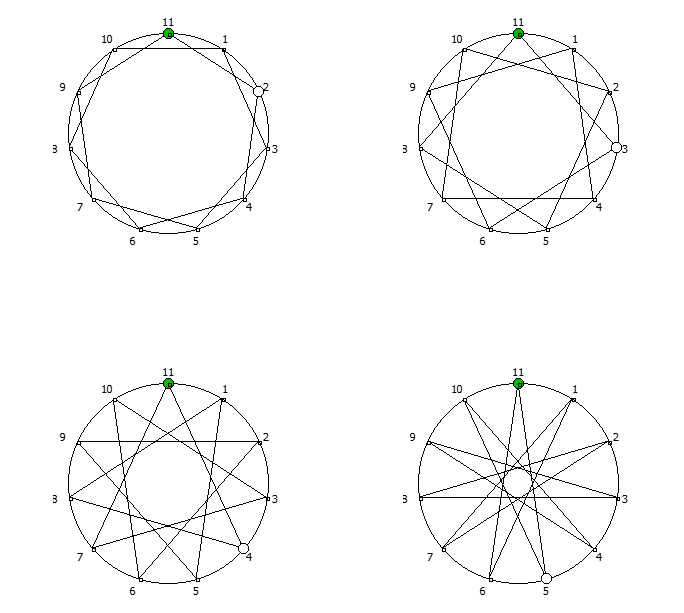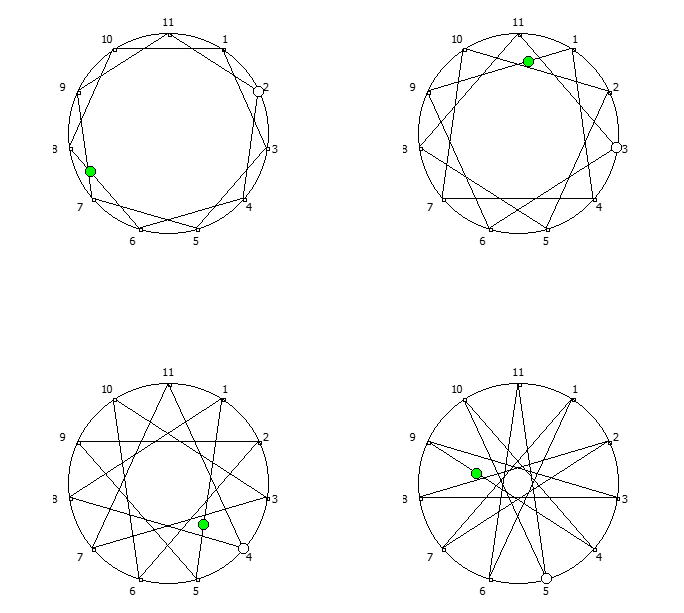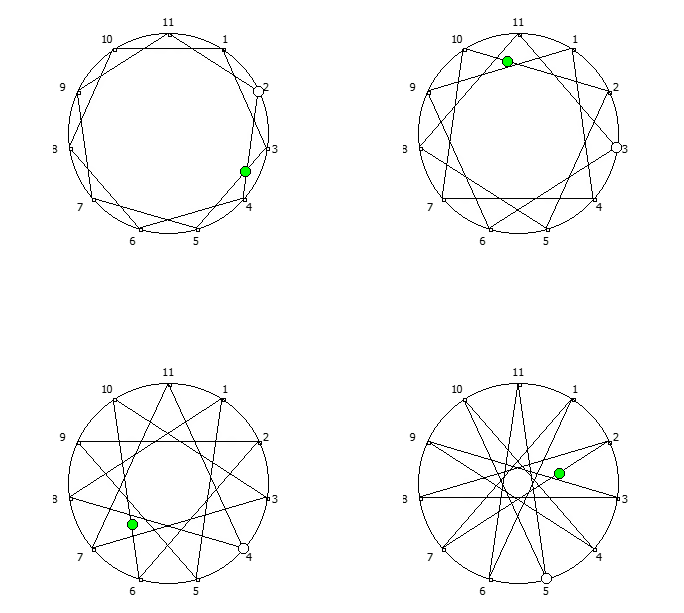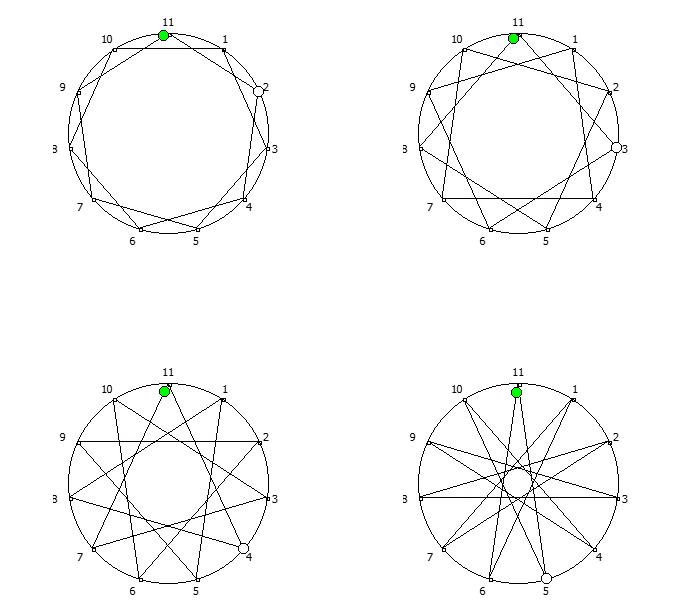
, :
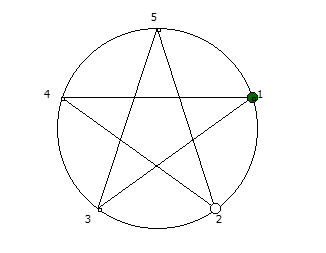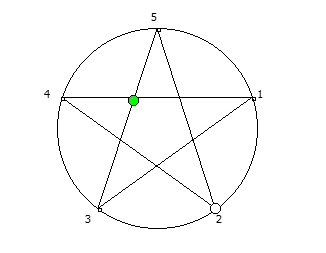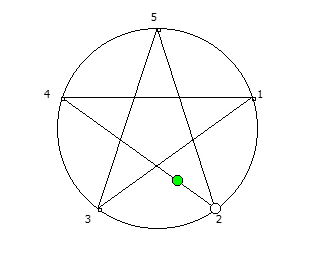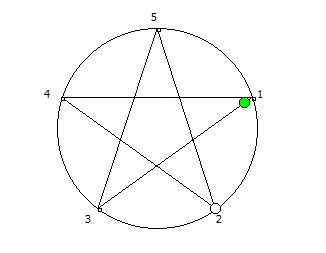
, . , [1, 3, 2, 6, 4, 5]. :
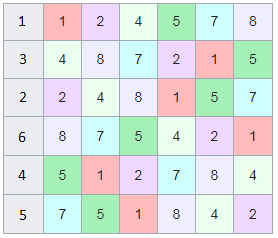
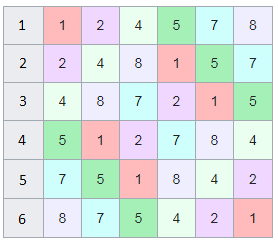
, 142857.
, , .
, n- , \ :)



, !
, , 90 1/91..90/91:

- , , !
Hope you were interested, thank you very much for your attention!