
Mathematics is the queen of sciences, it finds application in physics, chemistry, geography ... Including in armed conflicts. The course of sometimes wars was largely determined by the size of the army, technology, money, natural and human resources of the participating countries.
But sometimes the main thing is something completely different - intellect. During the Second World War, mathematicians not only participated in the development of weapons, but also actively helped to solve very specific problems. Sometimes mathematicians and scientists, on the contrary, stumbled upon a misunderstanding of military officials and state policy. Consider some episodes related to mathematics and the events of World War II: how mathematicians helped win battles or, completely unfairly, fell under the pressure of political repression.
Mathematics in Hitler's Germany
During the first two decades of the 20th century, Germany was the center of the international research community in the field of mathematics. This is largely the merit of David Hilbert, the greatest universal mathematician after the death of Henri Poincaré. In addition to his contributions to a wide variety of fields ( invariant theory , general algebra , mathematical physics , integral equations , foundations of mathematics ), Hilbert is known for formulating a list of 23 mathematical problems, which determined the vector of development of mathematics in the 20th century. The University of Göttingen, where, in addition to Hilbert, such famous mathematicians as Felix Klein, Hermann Minkowski, Dirichlet, Richard Dedekind worked, became a mathematical mecca, continuing the traditions of the mathematical school laid down by Gauss and Riemann.
However, the rise to power of the Nazis and repressive policies (for example, the Civil Service Law1933) greatly shaken the status of German science. The Nazis cleaned universities of "non-Aryan elements" by persecuting many talented scientists (among mathematicians, Edmund Landau and Isai Shur are vivid examples). Party functionaries did not understand the importance of fundamental science, which does not bring immediate results, especially in the military field. In addition, researchers who actively communicated with colleagues from abroad were skeptical about the policies pursued by the Nazis. As a result, many promising projects related to jet aircraft (Messerschmitt Me.262), missile "weapons of retaliation" (intercontinental missiles A-9 / A-10 in the framework of Project America and the partially-orbital bomber Silbervogel), the atomic bomb (the German nuclear program) were either delayed or (in most cases) not completed. And many scientists, including mathematicians, emigrated to the United States and Canada, which shifted the focus of the mathematical world from Europe to North America.
"Aryan" mathematics
Anti-Semitism was prevalent in the German academic environment before the Nazis came to power. However, scholars of Jewish origin still managed to make their way into the academic environment. A significant role in this was played by the above-mentioned David Hilbert, who held an international position. With his help, talented Jewish mathematicians such as Hermann Minkowski, Edmund Landau, Richard Courant and Emmy Noether were able to obtain full professorships.
In the 1920s, Hilbert found himself embroiled in an argument with the Dutch mathematician Brouwer, the founder of intuitionism. Brower criticized Hilbert's formalism, in particular the applicability in mathematical reasoning of the law of the excluded middle, the removal of double negation, and indirect proof (proof by contradiction). Later, the controversy turned into an ideological plane, when Brower called himself "a champion of Aryan Germanism." Hilbert expelled Brouwer from the editorial board of the Mathematische Annalen when he claimed that there were too many Ostjuden in the magazine (Eastern European Jews). Subsequently, Berlin sided with Brouwer: the Nazis in 1933 offered him a place at the University of Berlin, but Brouwer refused. After the war, it saved his career when he was accused of having links with the Nazi party.

David Hilbert
The magazine Deutsche Mathematik , published already under the Nazis and edited by the mathematician Ludwig Bieberbach, also criticized Hilbert's formalism and called for the "aryization" of mathematics. It was argued that "Aryan mathematics" would emphasize geometric mathematics and the theory of probability, and abstract axiomatics was declared "Franco-Jewish". Cantor's set theory, measure theory, and even abstract algebra came under suspicion. Bieberbach appealed to the psychological typology of Erik Jensch and attributed the abstract S-type of thinking to the Jews, and the J-type, striving to cognize reality in all its diversity, attributed to the Germans.
With the adoption of the Civil Service Law, about 200 professors of mathematics were expelled from the country. The victims included the algebraist Robert Remarque and the logician Curt Grelling. 75 professors of mathematics (Paul Bernays, Hermann Weil, Emmy Noether, Herbert Busemann and others) took refuge in the United States, raising a new generation of mathematicians, this time American.
Göttingen and Berlin ceased to be world centers of mathematics. One day, Bernhard Rust , the Nazi Minister of Education, asked Hilbert: "How is mathematics in Göttingen now, after freeing itself from Jewish influence?" Hilbert sadly replied: “ Mathematics in Göttingen? She is no more "
Z * and the first high-level programming language
With applied mathematics, things were better: after all, in the development of complex types of weapons (artillery, aviation, radio engineering, detection and guidance equipment), one cannot do without it. However, the successes were not only in the creation of innovative weapons. In Germany, the world's first workable software-controlled and freely programmable computer, developed by engineer Konrad Zuse, appeared.
In 1938, Zuse built the Z1 machine: the machine was completely mechanical and used binary logic in its work. The goal was calculations to improve the aerodynamic parameters of aircraft. The following year, the engineer upgraded the Z1 to Z2. This time, the machine performed calculations using electromagnetic relays. Both devices followed instructions from punched cards, which, by the way, did not know how to rewind (which did not allow organizing cycles in programs).

Z4 The
military authorities had nothing to do with Zuse's designs, so the engineer was called to the front in 1939. The officer in charge of conscription and release from service, said that such equipment is not needed, because " German aircraft are already the best in the world, there is nothing to improve ." However, the management of the company "Henschel" managed to beat the talented engineer back, having received an official state order for the computer proposed by Zuse. In 1941, the Z3 was created, which, unlike its predecessors, found practical application: it was used to calculate the vibration characteristics of wings and empennage in projected military aircraft.
The architecture of the Z3 was reminiscent of its predecessors. The machine consisted of 2,400 electromagnetic relays, 600 of which worked in a computing module, the rest played the role of a 64-word memory. The program was stored on plastic punched tape; according to some reports, ordinary film was used for this - defective takes and other wastes from the activities of film studios. Z3 knew how to work with floating point numbers (unlike Mark I, ABC or ENIAC) - for this Zuse developed a "semi-logarithmic notation" that corresponds to the modern representation of floating point numbers. A special feature is the separation of memory and processor. The main components of the Z3 are shown in the figure:
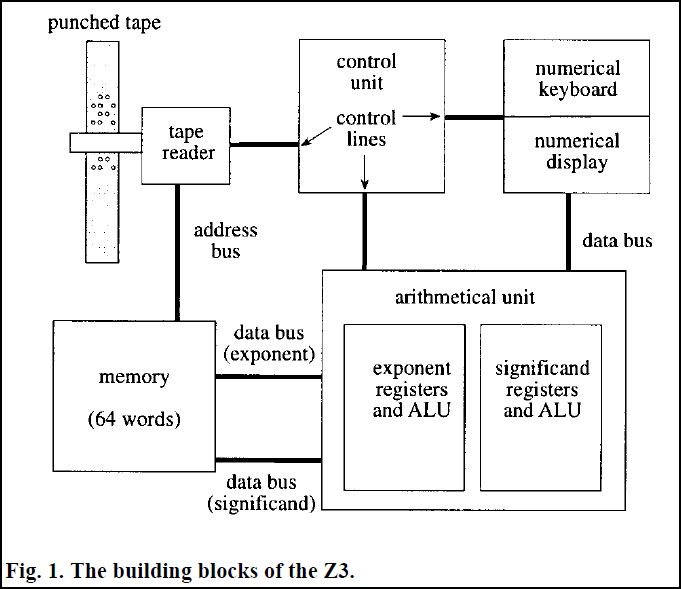
Interesting fact: Zuse asked for funding to replace the relay with electronic circuits (as in ENIAC), but he was refused. This time the machine was able to loop, but it lacked the conditional jump instructions. Finally, finally by 1944, the Z4 was almost finished, already allowing for branching. Unfortunately, Zuse's laboratory was hit by Allied bombing raids, which destroyed the first three models of the computing device.
It should be noted that Konrad Zuse also created the world's first high-level programming language - Plankalkül . The language supported assignment operations, subroutine calls , conditional statements , iterative loops , floating point arithmetic, arrays , hierarchical data structures, assertions, exception handling, and many other quite modern programming language tools .
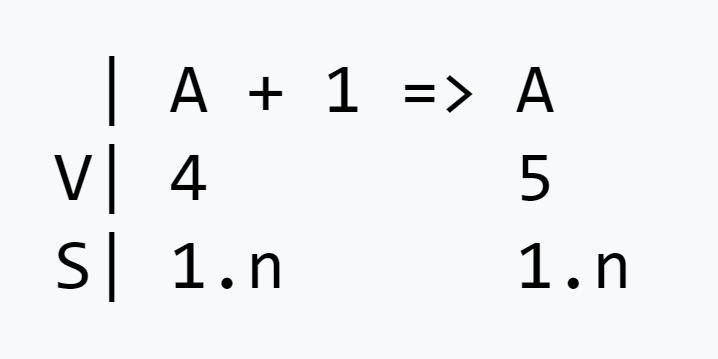
An example of assignment A [5] = A [4] +1 from the Plankalkül implementation of the 1990s
Mathematics in the countries of the Anti-Hitler Coalition
the USSR
After the beginning of the Second World War, many mathematicians went to the front. The remaining scientists, like the whole country, went over to "martial law". The tasks of increasing the effectiveness of the Red Army came to the fore. During the war, the following tasks were solved:
Optimization of the process of checking ammunition:
Checking the quality of ammunition during the Second World War sometimes took almost more time than manufacturing them. Based on the theory of probability, mathematician M.V. Ostrogradsky proposed a new method for testing them.
Navigation tables:
Mathematical team, under the leadership of S.N. Bernstein, in 1942 he developed tables for determining the position of the vessel by radio bearings. These tables made it possible to speed up the calculations tenfold.
Unsinkable tables:
A.N. Krylov developed unsinkability tables, by which it was possible to calculate how the flooding of certain compartments would affect the ship. The tables also made it possible to obtain information about which compartments needed to be flooded in order to eliminate the ship's roll. Eh, that would be such tables during the time of the Titanic.
Corkscrew, flutter and shimmy:
These strange words (especially the last two) refer to the world of aircraft. A corkscrew is a phenomenon where the plane starts to fall while spinning like a spin. Flutter is the occurrence of vibrations on the body of an aircraft when it picks up speed, leading to its destruction. Shimmy - landing gear vibrations during takeoff. All these phenomena have caused accidents more than once. M.V. Keldysh and his collaborators created a mathematical theory that protected aircraft from these phenomena.
Of course, these discoveries were not the only wartime mathematical problems solved. Also, many scientists have worked on the most optimal distribution of projectiles, both on the ground and in the air. Mathematics made a huge contribution to the development
USA
Survivor bias
During the Second World War, there was a statistical research group in the United States - SRG. Its goal was to collect the coolest American statisticians and use them to solve military problems. One of the tasks was formulated as follows:
“ If you do not want the enemy plane to shoot down yours, then you cover it with armor. But the armor makes it heavier, less fast and maneuverable, and fuel consumption increases. If there is a lot of armor on the plane, this is a problem, if not enough, it is a problem. It is necessary to determine the optimal solution . "
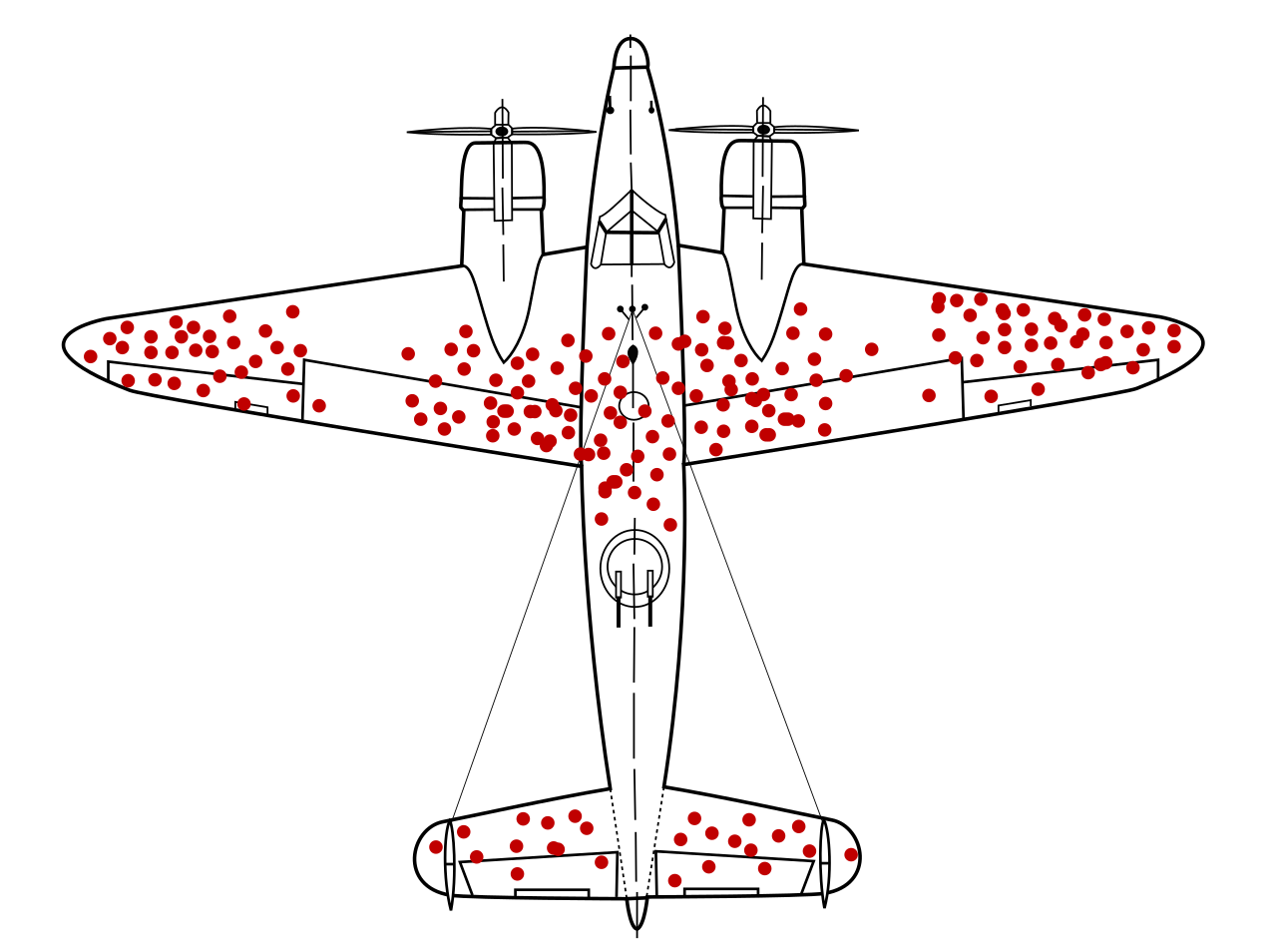
To solve this problem, the military provided SRG with data that, in their opinion, could help the group. The planes returning from Europe were covered with bullet holes, but not evenly. There were more holes in the hull than on the engine.

The command considered that it was necessary to strengthen the places of the aircraft, where there were the most penetrations. But it was necessary to understand where more armor was needed and where less. With this question, they turned to one of the SRG members - Abraham Wald. His answer was unexpected - it was necessary to strengthen those places in which there were the least number of holes. The reason why there were fewer holes in the engine than in the hull was not in the selectivity of the German army, but in the fact that aircraft with such damage simply did not return from battle. And the body, all in holes like cheese, can be left without additional armor. In the hospital, you will see more wounded in the limb, and not in the chest - not because they do not get into it, but because patients do not survive. In honor of this incident, the name was given to the systematic error of the survivor - a statistical error,in which the data of one group (of which there are many) are taken into account and another group (for which there is little data) is overlooked, although no less important information is hidden in the second group.
Great Britain
Fighting "Enigma"
Enigma is an electromechanical rotary encryption machine. It was used by Germany during the Second World War to transmit and decode encrypted messages. For military purposes, two versions of the Enigma were used - with 3 and 4 (in the Navy) rotors. Together they formed an electrical circuit. Depending on the initial settings of the machine, when the symbol was pressed, one of the rotors turned and generated an encoded symbol. The encoding of each next character depended on the previous one. At the exit, the operator received an encrypted message that could be decoded using a similar machine if there were initial settings - a code. Germany changed this code daily.
The first successes with deciphering the enigma messages were achieved by Polish scientists in 1939. They managed to decipher some of the messages, but failed to fully solve the riddle. After Poland was captured, these scientists fled, first in France, and then moved to Great Britain and transferred their developments to local specialists.
The British group led by Alan Turing faced a new problem. Before the start of the war, the Germans increased the number of rotors from which they could choose three (or four) for work. In 1940, the first copy of the electronic-mechanical machine for decoding the enigma, the Bombe, appeared. Its principle of operation was to emulate the work of several enigma machines and discard conflicting and meaningless options. The human factor was also used in the work of Bombe: procedural flaws, the known text of messages (for example, when transmitting weather reports). By the end of the war, about 210 machines had been created, which decoded up to 3000 messages daily. It is worth noting that the main information encoded by the enigma was of an operational-tactical nature, and the Germans used other methods to transmit messages of the "high echelon".

While working on Bombe, the team faced pressure from management more than once. Basically, it was caused by the secrecy of the operation and the cost of the project. But politicians should not be condemned - such pressure was more likely a trend of events, and not a simple whim of bureaucrats.
Random distribution
During the war, the Luftwaffe constantly bombed London. Until June 13, 1944, these were ordinary bombings, but it was on June 13, a week after the Allied landings in Normandy, that a new type of missile - jet rockets - flew to London. "V-1" or "V-1" - the first cruise missile, used in real combat. Because of the characteristic feature of the engine, they were nicknamed "buzzers". Between June and October 1944, 9521 missiles were fired towards Great Britain, of which 2419 reached their target. Due to the technologically advanced design and slogans of Germany, the British wondered whether these missiles fell by accident or not? Mathematicians came to the aid of Great Britain with statistics. After analyzing the location of the explosions, they came to the conclusion that these missiles fall at random.

V-1
Epilogue
Typically, the winner is the one who has 5% fewer planes shot down, or uses 5% less fuel, or who provides the infantry with 5% better food for 95% of the cost. It is not customary to talk about such things in war films, but the wars themselves boil down to them. And at every stage of this path, there is mathematics. - J. Ellenberg, “How not to be mistaken. The Power of Mathematical Thinking ”.
After the war, some of the unique designs passed into civilian use. The work of Turing, von Braun and many other scientists has found applications in peacetime technologies: jet aircraft, rocket science, nuclear power, and computers. It is not clear how progress would have turned without the discoveries and works of these scientists, made under the influence of wartime.
Cloud servers from Macleod are fast and secure.
Register using the link above or by clicking on the banner and get a 10% discount for the first month of renting a server of any configuration!
