🙎🏼 👩🏽‍🤝‍👩🏻 🧙 What if gravity and the accelerated expansion of the universe are a consequence of entropy? 👩🏼‍🤝‍👨🏿 💅🏾 👨🏿‍⚕️

Foreword

Attraction reigns over long distances, it is universal and obvious in comparison with other interactions, but the nuance is that it is incredibly weak - 10 ³⁹ times weaker than electromagnetic interaction, and its effect at the microscopic level is completely invisible. The nature of gravity in the world of elementary particles has been breaking the minds of scientists for several decades, because it does not want to put up with either quantum physics or electrodynamics. String theory also cannot satisfy the conflict of gravity with other interactions. But it seems we have found a way to reconcile gravity with physics. How? Assume that she is not a fundamental interaction.

. . - .

, , . . : . .. , , .

— , (0 1), . , .

? , . , , — . , — , , , , — . . , , , , , . .

Stephen Hawking, Credit: New Scientist — , Credit: New Scientist

. , n- i- (n-1)- , . — , . — . , . .

The 5-dimensional anti-Dessiter space-time is enclosed in a 4-dimensional sphere of flat geometry (holographic screen). The processes occurring inside the sphere and on the surface of the sphere are different: for example, the behavior of superstrings in a five-dimensional space for a four-dimensional one is reflected in the form of the interaction of conformal fields, and a black hole, which cannot exist in such a four-dimensional sphere, completely turns into hot radiation. — 5- - 4- ( ). : , , , , .

?

, , , . , , , n- -, , (n-1)- , . ? . , - .

, , 2010 — « ». . .

, , — , . , . , . , , .. — . , , . — , , , , , .

m, x S. . :

$\Delta S = 2\pi k_ \dfrac{mc}{\hbar} \Delta x.$

— , :

$\Delta F \Delta x = T \Delta S,$

T — .

, , . , :

$k_ T = \dfrac{1}{2\pi} \dfrac{\hbar a}{c},$

a — , k — , h — . :

, E . , . N :

$N = \dfrac{1}{2} Nk_ T .$

(, , ):

m — , . , :

$A = 4 \ pi R ^ 2,$

$F = G \ dfrac {Mm} {R ^ 2},$

G — .

, , , . , , — (Easson et al.), . , . — .

, . a(t) FLRW- :

$H (t) ^ 2 = \ left (\ dfrac {\ dot a} {a} \ right) = \ left (\ dfrac {8 \ pi G} {3} \ right) \ rho,$

, ρ — , , :

$\ rho = \ rho_m + \ rho _ {\ gamma},$ $\ rho_m (t) = \ rho_m (t_0) a (t) ^ {- 3},$ $\ rho_ {DE} (t) = \ rho_ {DE} (t_0) a (t) ^ {- 3 (1+ \ omega)},$

$\ omega = \ dfrac {p} {\ rho c ^ 2}.$

, (-1), :

$a (t) = a (t_0) e ^ {Ht},$

$H = \ sqrt {\ dfrac {\ Lambda} {3}} = \ sqrt {8 \ pi G \ rho_ {DE}}.$

$\ dfrac {\ delta ^ p} {\ delta t ^ p} a (t) = H ^ p, \: t \ rightarrow 0.$

$a (t) = a (t_0) e ^ {Ht},$

$\ sqrt {3} H = \ sqrt {\ Lambda} = \ sqrt {8 \ pi G \ rho_ {DE}}.$

10¹⁸ ⁴. 10^-3⁴ — 120 ! . :

$T _ {\ beta} = \ dfrac {\ hbar} {k_B} \ dfrac {H} {2 \ pi} \ sim 3 \ times 10 ^ {- 30} K.$

, , , :

$a_ {horizon} = \ dfrac {2 \ pi c k_B T _ {\ beta}} {\ hbar} = cH \ sim 10 ^ {- 9} \: m / s ^ 2.$

, — . Ia. :

$D_L = \ dfrac {c (1 + z)} {H_0} \ int ^ z_0 \ dfrac {\ delta z '} {H (z')}.$

, , , , .

, , :

, — . , , , , . , , — , , . , . , - — , . , . :

();
« » Modern Cosmology ();
(), ();
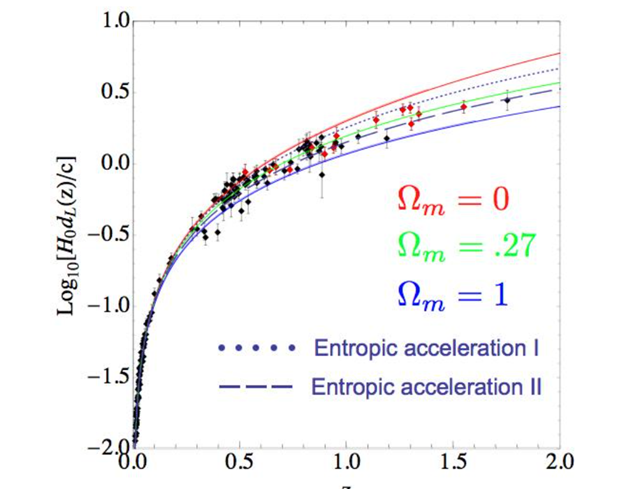
«Entropic Acceletating Universe» arXiv.org (Easson et al., );
« — » Modern Cosmology ();
« : » ();
« » ();
Superfood article on the holographic principle in English ( link ).

Well, I also remind you that the reader does not hesitate to ask a question or correct me in the comments. I also have a telegram channel where I talk about the latest news in cosmology and astrophysics, as well as write about astrophotography. Write to me in a personal or our chat . All good!

What if gravity and the accelerated expansion of the universe are a consequence of entropy?

Foreword

?

More articles: