Post # 3 for beginners is devoted to generating distributions, their properties, and graphs for their comparative analysis.
Baker and Poincaré
There is a legend, almost certainly apocryphal, which makes it possible to consider in more detail the question of how the central limit theorem allows one to reason about the principle of the formation of statistical distributions. It concerns the renowned 19th century French polymath, Henri Poincaré, who, legend has it, spent one year every day weighing a fresh loaf of bread.
At that time, baking was regulated by the state, and Poincaré found that although the results of weighing loaves of bread obeyed a normal distribution, the peak was not at the publicly advertised 1 kg, but at 950 g. He informed the authorities about the baker from whom he regularly bought bread. and he was fined. This is the legend ;-).
The following year, Poincaré continued weighing loaves of bread from the same baker. He found that the mean was now 1 kg, but that distribution was no longer symmetrical around the mean. It has now been shifted to the right. This was consistent with the fact that the baker now only gave Poincaré the heaviest of his loaves of bread. Poincare again reported the baker to the authorities and the baker was fined a second time.
Whether it really was or not is not important here; this example just serves to illustrate a key point - the statistical distribution of a sequence of numbers can tell us something important about the process that created it.
Generating distributions
, , stats.norm.rvs. (rvs . normal variates, .. ). 1000, 1 . , 30.
def honest_baker(mu, sigma):
''' '''
return pd.Series( stats.norm.rvs(loc, scale, size=10000) )
def ex_1_18():
''' '''
honest_baker(1000, 30).hist(bins=25)
plt.xlabel(' ')
plt.ylabel('')
plt.show()
, :

, . ( « ») :
def dishonest_baker(mu, sigma):
''' '''
xs = stats.norm.rvs(loc, scale, size=10000)
return pd.Series( map(max, bootstrap(xs, 13)) )
def ex_1_19():
''' '''
dishonest_baker(950, 30).hist(bins=25)
plt.xlabel(' ')
plt.ylabel('')
plt.show()
, :
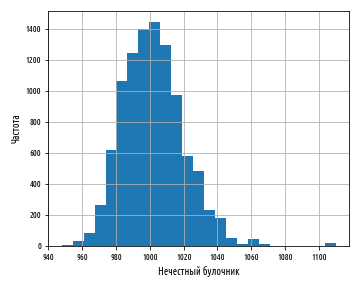
, , , . - 1 , . , .
. , , , . , , , .
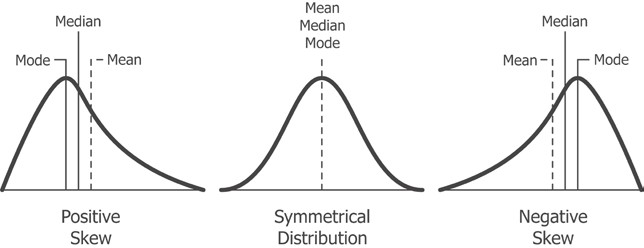
pandas skew
:
def ex_1_20():
''' '''
s = dishonest_baker(950, 30)
return { '' : s.mean(),
'' : s.median(),
'': s.skew() }
{'': 0.4202176889083849,
'': 998.7670301469957,
'': 1000.059263920949}
, 0.4. , .
. , quantile
0 1 . 0.5- .
, . , -, Q-Q, . Q-Q plot. . , , . , .
. qqplot
, :
def qqplot( xs ):
''' ( -, Q-Q plot)'''
d = {0:sorted(stats.norm.rvs(loc=0, scale=1, size=len(xs))),
1:sorted(xs)}
pd.DataFrame(d).plot.scatter(0, 1, s=5, grid=True)
df.plot.scatter(0, 1, s=5, grid=True)
plt.xlabel(' ')
plt.ylabel(' ')
plt.title (' ', fontweight='semibold')
def ex_1_21():
'''
'''
qqplot( honest_baker(1000, 30) )
plt.show()
qqplot( dishonest_baker(950, 30) )
plt.show()
:

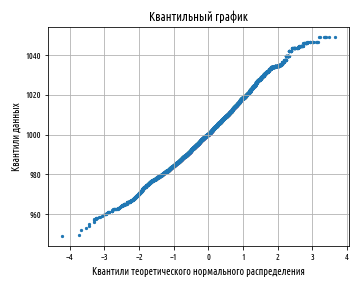
. :
, , , ; . , :

: , , , , ,
. ( ) .
() . , . , , .
, « », — , . :
def ex_1_22():
'''
'''
d = {' ' :honest_baker(1000, 30),
' ':dishonest_baker(950, 30)}
pd.DataFrame(d).boxplot(sym='o', whis=1.95, showmeans=True)
plt.ylabel(' (.)')
plt.show()
:

. — . — . , , . , .
. . , .
(), , . Cumulative Distribution Function (CDF), , , , x. , 0 1, 0 — , 1 — . , , . , 6?
5/6. , , , 1/6. — 50%.
, — , . , , , .
— . 0.5- 1000, 1000 0.5.
, pandas quantile
, empirical_cdf
0 1. , .. ( ) , , , , .
— , .
. pandas plot
, — — , . plot
, x y . pandas DataFrame
.
, plot
. pandas , . plot
, (ax
) plot
, (ax=ax
). . , . , (tp[1]
tp[3]
) , :
def empirical_cdf(x):
''' x'''
sx = sorted(x)
return pd.DataFrame( {0: sx, 1:sp.arange(len(sx))/len(sx)} )
def ex_1_23():
'''
'''
df = empirical_cdf(honest_baker(1000, 30))
df2 = empirical_cdf(dishonest_baker(950, 30))
ax = df.plot(0, 1, label=' ')
df2.plot(0, 1, label=' ', grid=True, ax=ax)
plt.xlabel(' ')
plt.ylabel('')
plt.legend(loc='best')
plt.show()
:
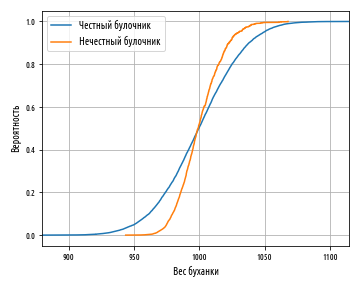
, -, , . , 0.5, 1000 . , .
Github. .
, 4, «Python, » .