The translation was prepared as part of the " Machine Learning. Professional " course .
We also invite everyone to take part in the two-day online intensive "Deploy ML models: from dirty code in a laptop to a working service".
Observation errors and subgroup differences cause statistical paradoxes
Observation errors and subgroup differences can easily lead to statistical paradoxes in any data science application. Ignoring these elements can completely discredit the conclusions of our analysis.
Indeed, it is not uncommon to see such astonishing phenomena as subgroup trends that reverse completely in the aggregated data. In this article, we'll take a look at the top 3 most common statistical paradoxes found in Data Science.
1. Burkson's paradox
The first striking example is the inverse correlation between severity of COVID-19 disease and cigarette smoking (see, for example, the European Commission's Wenzel 2020 review ). Cigarette smoking is a well-known risk factor for respiratory disease, so how do you explain this controversy?
Griffith 2020, Nature, , (Collider Bias), . , , : «».
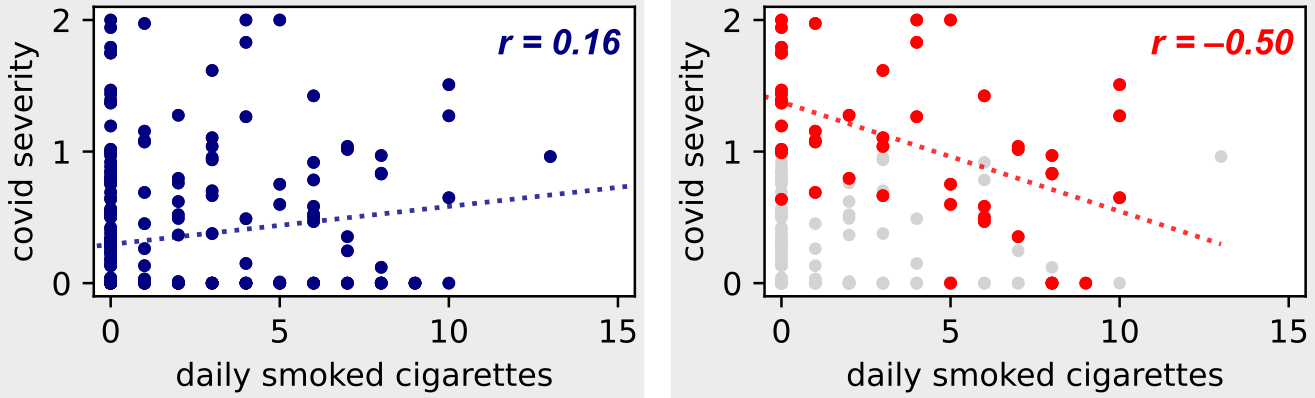
: «» — - « », « COVID-19». ( )
«» . , COVID-19 . , , , .
. , ( -).
: «», COVID-19! ( )
COVID-19 , , , .
— — ! , .
COVID-19 . , 1, .
(- , , ), - .
, COVID-19, ! , COVID-19 - , (, - , , ).
Berkson 1946, , , .
2. ()
. - - (, , ), , .
, , , , , . , ( — . ), : , !
, . : « ».

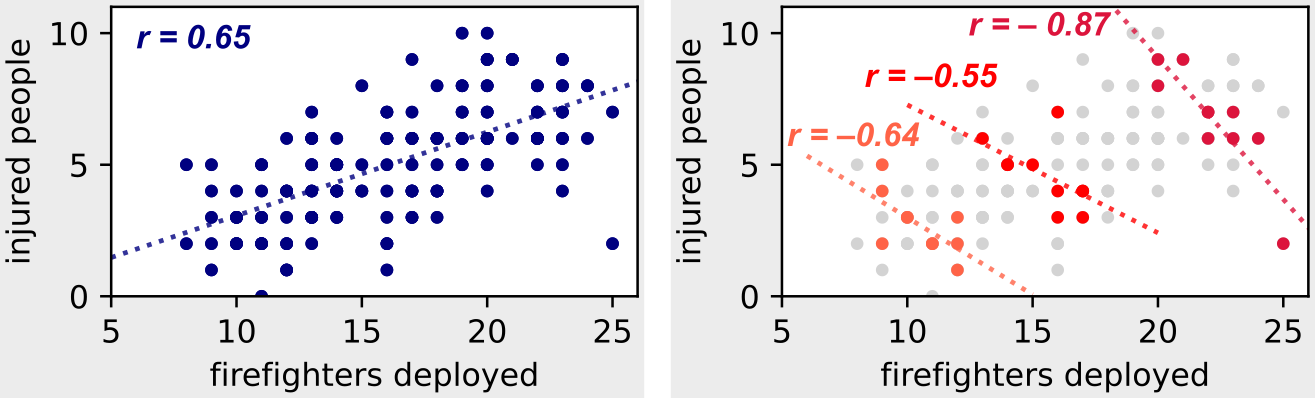
: « » — «n » «n ». ( )
. , , , , .
. , , (.. ).
: « », ! ( )
, , , .
, , .
, , , .
3.
— , - , , . .
1975 , , , .
, , , .
, , .
, , : A B.
100 : 80 A, 68 (85%), 20 , 12 (60%).
100 : 30 , 28 (93%), 70 B, 46 (66%).

: - , ! ( )
.

: , . ( )
, , . , ( A: 80–30, B: 20–70). , B ( ), ( ). , .
, -, data science. .
"Machine Learning. Professional"
- « ML : »