☦️ ♀️ 🧓🏽 A new class of prime numbers that I discovered by accident 👩‍👩‍👧‍👧 👨🏿‍🏭 ✌️

Hello everyone! This is my first post on Habré, so I will introduce myself: my name is Kostya, I am a C ++ developer, a bit of a musician, a beginner ML engineer and a lover of mathematics. As you might guess, this post will be about my math hobby.

UPD: Conclusions have been added. A little later, I will add examples of other primes and other number systems that will be used to generate cyclic numbers, and as a consequence, cyclic primes.

Background: about 14 years ago, I encountered the phenomenon of cyclic numbers, I was fascinated by the patterns that are formed in them and promised myself to explain them. At first, I made naive attempts at analysis, which brought very mediocre results, but in 2016 I was able to see for myself that the rational fraction 1/7 can be represented by a converging geometric progression. To be honest, at that moment I did not even understand that it was a geometric progression, but I recognized it visually. In 2018, I decided to put all my skills and diligence to find as many patterns of cyclic numbers as possible. I found a lot, but now I want to share what I consider to be the most important, and ironically, I found by accident: a new class of prime numbers.

I was researching full reptend prime, prime numbers, and to be more precise - such number systems for prime numbers, in which 1 / P, where P is a prime number, will give a periodic fraction, the period of which will be equal to the cyclic number.

Here you should probably give the very definition of a cyclic number:

A cyclic number is an integer whose cyclic permutations are the product of that number and consecutive numbers.

— 142857, "" + . , . , , , . , " . ".

142857 * 2 = 285714

142857 * 3 = 428571

142857 * 4 = 571428

142857 * 5 = 714285

142857 * 6 = 857142

, 142857 2 6, 142857. .

, 1/7 . 1/7, . .

1/7 . ! , , - , .

, , , 7 . - .

, full reptend prime, «The Philisophy of Arithmetic: Exhibiting a Progressive View on the Theory and Practice of Calculation».

200 , . « », 1/7 .

«History of the Theory of Numbers» , full reptend prime.

«The Penguin Dictionary of Curious and Interesting Numbers» repunit.

«The Book of Numbers» , .

, , , , . .

, 142857, 1428571, . . , 1428571 1, — 7.

, 142857, ( 10 ). , .

7 , 142857: 1428571, 71428571, 7142857142857, 571428571428571, 1428571428571428571428571, 28571428571428571428571428571, 7142857142857142857142857142857.

: 7, 8, 13, 15, 25, 29, 31.


2	34
4	41
7	104
5	273
5	304
1	355
7	440
7	571
1	823
7	2215
5	2523
4	4379
2	4510
4	7553
4	7679
7	9536

23 , 10¹⁰⁰⁰.

. Full reptend prime

, , , , .

full reptend prime long prime. . , , full reptend .

full reptend

P — , , 1/P, N , P-1, , P N full reptend.

P full reptend N, P-1 .

P, , . P, - , P - full reptend prime.

P = 7 . 1/P = 0,(142857). 6, P-1. 1/P .. P-1/P:

2/P = 0,(285714)

3/P = 0,(428571)

4/P = 0,(571428)

5/P = 0,(714285)

6/P = 0,(857142)

, . . , . , . - 1/P. full reptend.

P 1/P. P. P = 2 2, P = 3 3, ..

( ⁿ) mod P = 1

P :

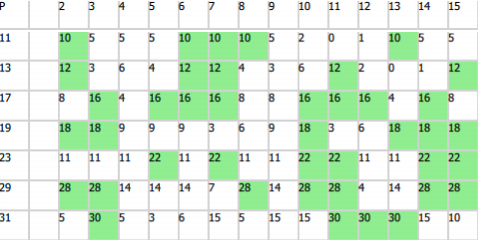
, , full reptend, 7, 17, 19, 23, 29. 2 5 , .

P = 3 : 1/3 = 0,(3). P = 11 , 2 : 1/11 = 0,(09).

P = 13 , 6, P-1. (P-1)/2, , . P 2nd reptend level prime. 2nd reptend level prime:

1/13 = 0,(076923)

2/13 = 0,(153846)

P = 13, P-1/P, , 1/13 2/13, .

3/13 = 0,(230769) — 1

4/13 = 0,(307692) — 1

5/13 = 0,(384615) — 2

6/13 = 0,(461538) — 2

7/13 = 0,(538461) — 2

8/13 = 0,(615384) — 2

9/13 = 0,(692307) — 1

10/13 = 0,(769230) — 1

11/13 = 0,(846153) — 2

12/13 = 0,(923076) — 1

2nd reptend level prime : .

.. : 769230769, 769230769230769230769,769230769230769230769230769230769.

: 1538461.

, , full reptend prime, . P = 7 2 , full reptend, 3 5 — .

7 . 12, . , 17 19, 59 61.

, full reptend n-th repntend level . P N .

1/P:

$\ begin {equation} \ sum \ limits_ {n = 0} ^ \ infty \ frac {s * r ^ n} {base ^ {length (n + 1)}} = \ frac {1} {P} \ end { equation}$

s — , 1/P:

$\ begin {equation} s = [\ frac {1} {P} * base ^ {length}] \ end {equation}$

full reptend prime , 1 . :)

length , s, . length .

r , 1/P. 1/P P-1, full reptend , P-1.

, , , . P= 7, .. full reptend .

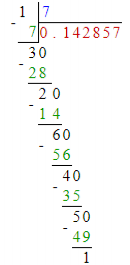
: [3, 2, 6, 4, 5, 1]. . base mod P. , :

$\ begin {equation} \ begin {cases} r_0 = 1 \\ r_n = r_ {n-1} * (base \ mod P) \\ \ end {cases} \ end {equation}$

$\ begin {equation} r_ {length} = base ^ {length} \ mod P \ end {equation}$

, : P— ; base — ; length — , .

$\ begin {equation} \ frac {1} {P} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {[\ frac {1} {P} * base ^ {length}] * (base ^ { length} \ mod P) ^ n} {base ^ {length (n + 1)}} \ end {equation}$

P = 7 c s, :

$\ begin {equation} \ frac {1} {7} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {1 * 3 ^ n} {10 ^ {n + 1}} \ end {equation}$

s = 1, 0,(142857), .. length = 1. r = 3, , length = 1.

$\ begin {equation} \ frac {1} {7} = 0.1 + 0.03 + 0.009 + 0.0027 + 0.00081 + .. \ end {equation}$

3 10. :

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14*2^n}{10^{2(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = 0.14 + 0.0028 + 0.000056 + 0.00000112 + .. \end{equation}$

2 100. s = 14, 0,(142857), .. length = 2. r = 2, , length = 2. , , , .

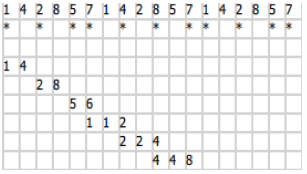
length 1:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142*6^n}{10^{3(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428*4^n}{10^{4(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14285*5^n}{10^{5(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142857*1^n}{10^{6(n+1)}} \end{equation}$

, s :

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428571*3^n}{10^{7(n+1)}} \end{equation}$

s - , . . .

, , , s P N — .

P = 17:

$\begin{equation} \frac{1}{17} = \sum\limits_{n=0}^\infty\frac{5*15^n}{10^{2(n+1)}} \end{equation}$ $\ begin {equation} \ frac {1} {17} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {58 * 14 ^ n} {10 ^ {3 (n + 1)}} \ end { equation}$ $\ begin {equation} \ frac {1} {17} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {588 * 4 ^ n} {10 ^ {4 (n + 1)}} \ end { equation}$

89 . 1/89 = 0,0112359.. — , . , :

$\ begin {equation} \ frac {1} {89} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {1 * 11 ^ n} {10 ^ {2 (n + 1)}} \ end { equation}$ $\ begin {equation} \ frac {1} {89} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {Fibonacci (n)} {10 ^ {n + 1}} \ end {equation}$

, — 109.

1/89 : (-1)ⁿ⁺¹. , , .

$\ begin {equation} \ frac {1} {109} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {9 * 17 ^ n} {10 ^ {3 (n + 1)}} \ end { equation}$ $\ begin {equation} \ frac {1} {109} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {Fibonacci (n) * (- 1) ^ {n + 1}} {10 ^ {n +1}} \ end {equation}$

, , .

-

s , , .

, P = 7, 142857, 1428571. , , 1/P, 1/P .. P-1/P. , , 71428571.

, . , . , , , , , .

, s, , , , . - .

P = 7. 1/P, P-1/P, , s : 2, 5, 7, 71, 571, 2857, 28571.

, - .

- P N. , full reptend prime .

,

, . P N, . , P, , .

- :

, P, , . , 142857. 40 5SMYBH ( 5, 28, 22, 34, 11, 17).

, , H5SMYBH 40 , , : 70217142857.

, . , , , .

P=7 N=10:

1) 1428571

2) 71428571

3) 7142857142857

4) 571428571428571

5) 1428571428571428571428571

6) 28571428571428571428571428571

7) 7142857142857142857142857142857

8) 2857142857142857142857142857142857

9) 42857142857142857142857142857142857142857

40 :

1) MCYB

2) Ra2YB

3) 13NYIMYBH

4) 277Sb5SMYB

5) 1D8TJS2CYBH5SMYB

6) GP98QAT0SMYBH5SMYB

7) 2NbRO471EIMYBH5SMYBH

8) PdGa11UDOPSMYBH5SMYBH

9) 3WAEQ3OR61AQVH5SMYBH5SMYBH

P=7 N=10 :

1) H5SMYBH

2) - 77 , 5SMYBH, B:

5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYB

1) 70217142857

– 12 , 123 .

2) 3262280440470765442418939358741703168874849426...

...28571428571428571428571428571428571428571428571428571428571428571428571428571

- , .

,

P = 7 N = 10. :

Ns(i) = N + 3*N*i + ((i + 1) % 2) * i*N*4

i — . i = 0 , full reptend prime. .

, , .

N = 3, 10, 17, 31, 38, 59:

Ns(i) = N + 3*N*i + ((i + 1) % 2) * i*N

N = 5, 19, 26, 33, 47, 61:

Ns(i) = N + N*i + ((i + 1) % 2) * i*5*N

N = 12:

Ns(i) = N + N*i + ((i + 1) % 2) * i*5*N

N = 40 , N = 10.

N = 24, N = 12.

, , N.

, 40 , . , , - , 40, , 40 .

12 24 . , , , 12.

, , , full reptend.

, , , 40 10 .

P = 5, . P = 17 , , base, base*2, base*4, .

, , .

, , . . .

, , . . : , , , , .

#1: 40 . 1/7₄₀=0.(5SMYBH)₄₀, H5SMYBH₄₀, 70217142857. 7142857, 40 .

#2: 10 . 571428571428571. 40 1D8TJS2CYBH5SMYB₄₀. , YBH5SMYB , .

,

, . . , .

, . , .

, full reptend prime .

. , , github. .

, full reptend prime. .

, , , .

, 2019 , \ .

, , arxiv.org – . , . – :

, arxiv ? ? 6- , .

Thank you all for your attention! I hope my first article was not tedious, there are a few more ahead and not all of them will be about mathematics.

A new class of prime numbers that I discovered by accident

. Full reptend prime

full reptend

-

,

,

,

More articles: