The Pauli exclusion principle with a single-valued many-particle wave function is equivalent to the requirement that the wave function be antisymmetric with respect to particle exchange . How to explain this on the fingers? Easy - poke your finger at the table, at the monitor, at something solid. Pierced deep into matter? Have you achieved overlapping finger and table atomic electron clouds? Not? Not surprising. Read on to find out why.
Spin
Quote from Wikipedia: The Pauli exclusion principle ( Pauli exclusion principle or simply the exclusion principle ) is a quantum mechanical principle that states that two or more identical fermions (particles with half - integer spin ) cannot simultaneously be in the same quantum state in quantum system .
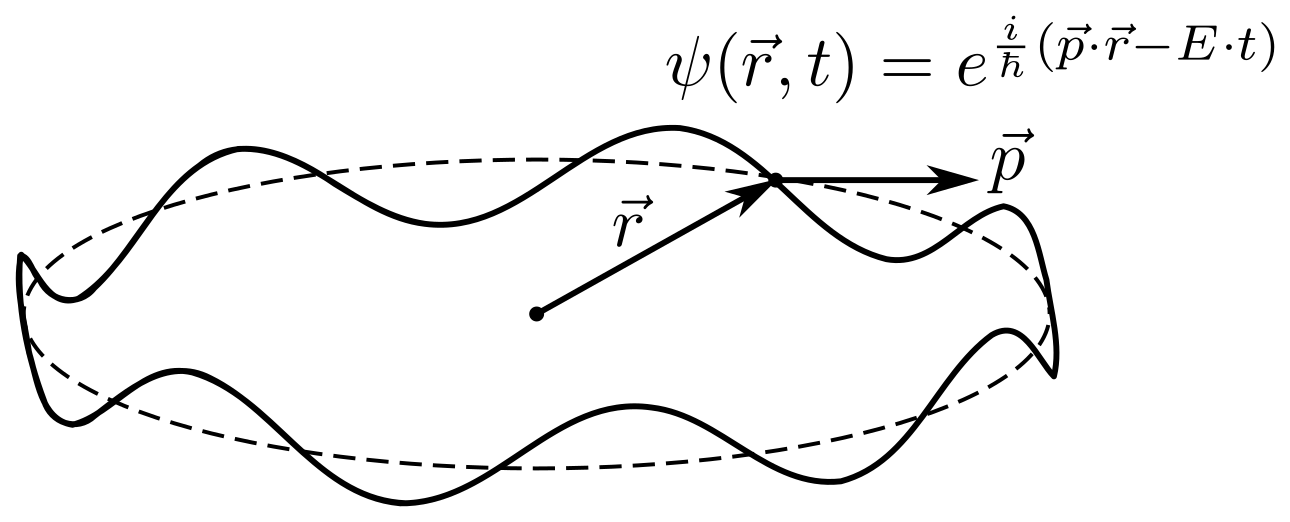
Something about spin. Let's start with what a spin is , in particular a half-integer spin . Let the particle move along the circumference of the length , and through
we denote the position of the particle. The particle will be described by a wave function
. For simplicity, we will assume that this is the most common traveling wave.
The wave function should be uniquely determined on the circle, and the rotation on
radian should not change it in any way, that is:
The imaginary exponent is a trigonometric function, like sine or cosine, in fact we wrote that the wave function is periodic . This is only possible if the work
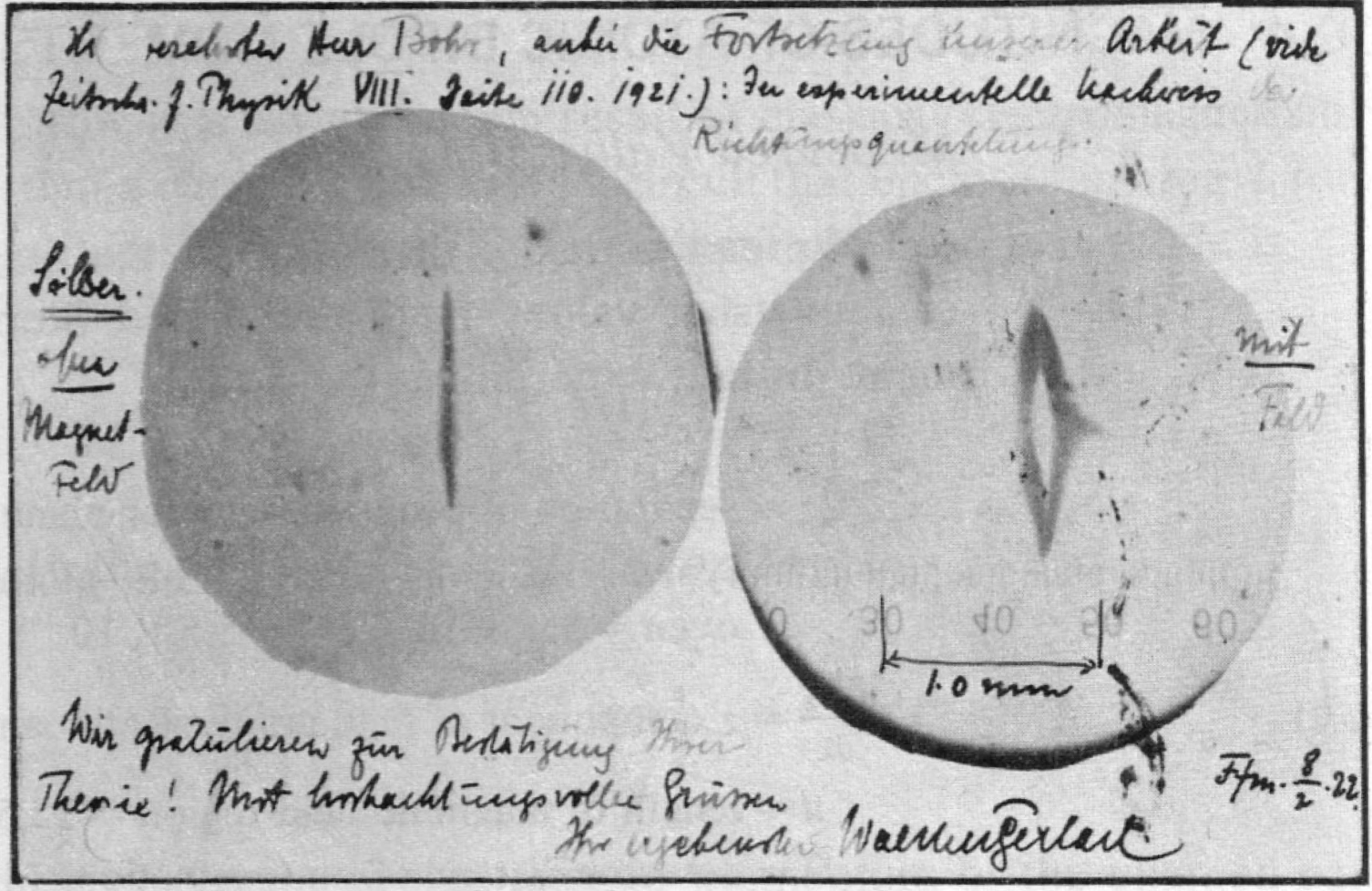
, , , , . , . n=1/2 . : , , , - Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics.

360 . , - . :
.
[. Pauli principle in Euclidean geometry]. , . - .
, . . 103(1) (1971) 155-179. :
,
.
. :
, . :
:
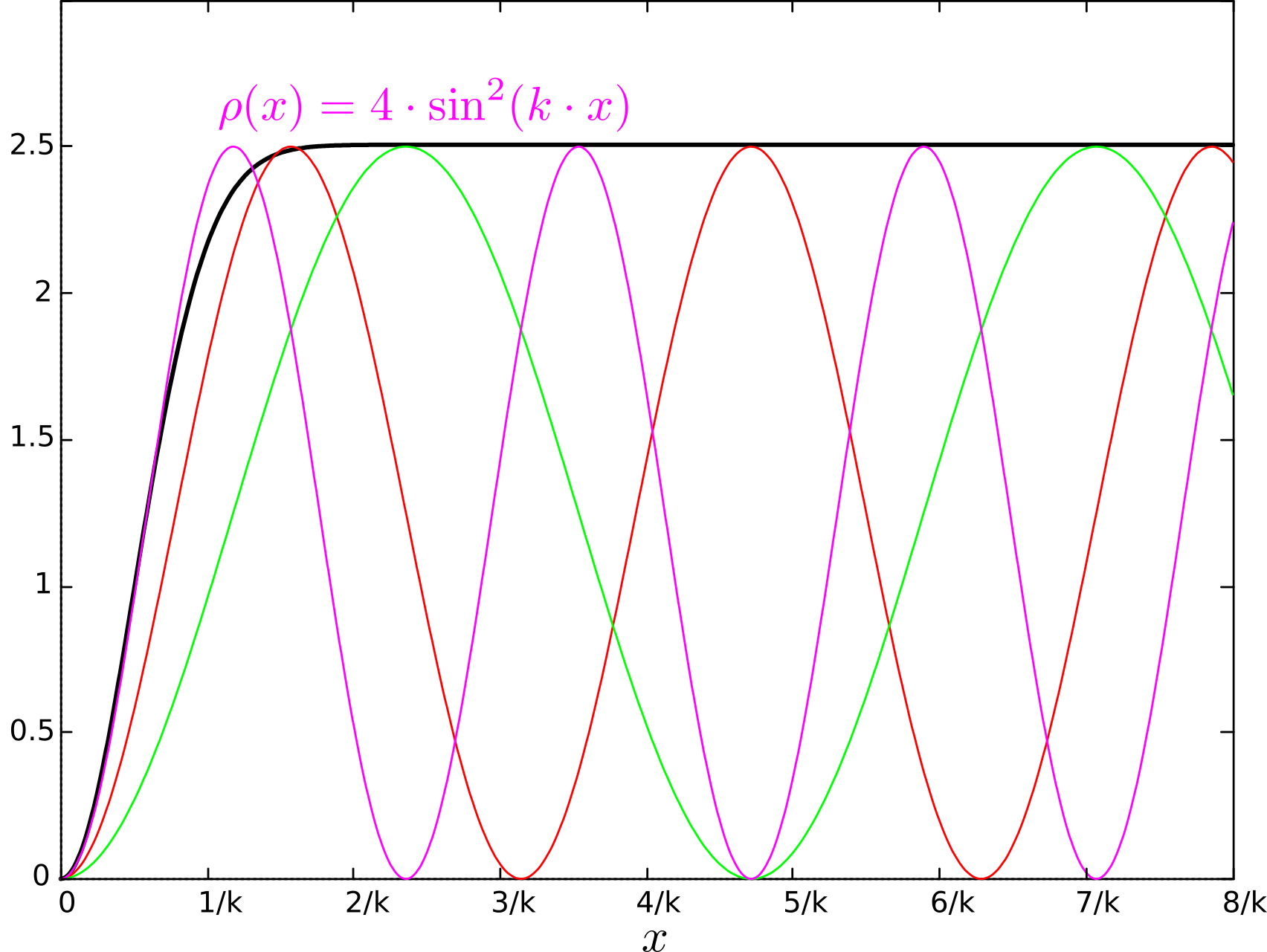
. , , , ..
. , . - .

- , .. , . - , , . . ( . Stevens, P.S. A Geometric Analogue of the Electron Cloud. Proceedings of the National Academy of Sciences 56(3) (1966) 789-793.) .
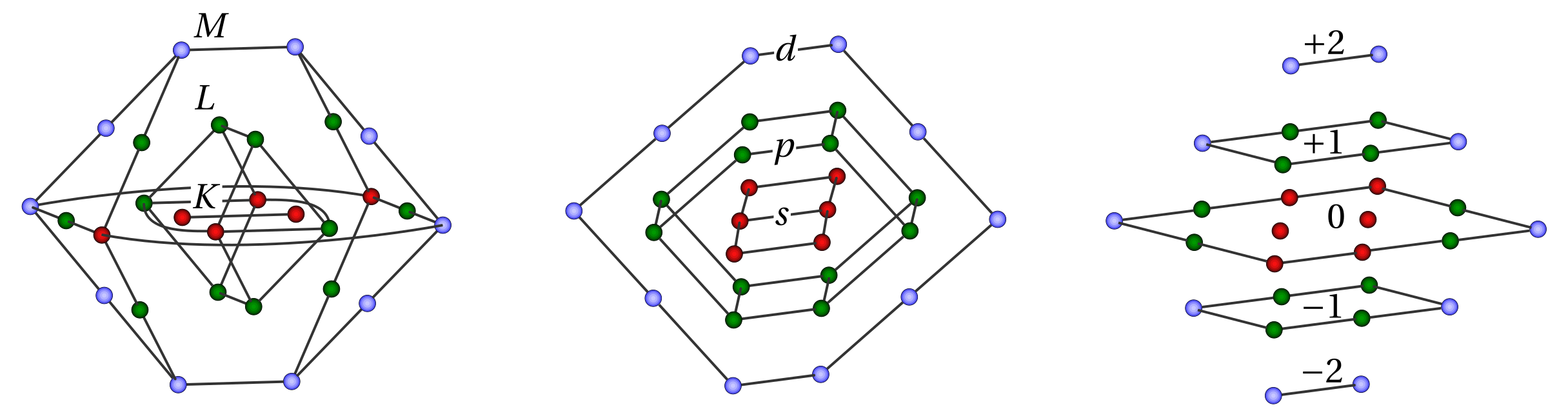
, - (/, +1/2 -1/2), , ( ) .
, , , . , , , . .
,
1961 (. ., . . .: "" 1976. . 197). , . , , - . , , .. 4+4=8, . , , , . , , :
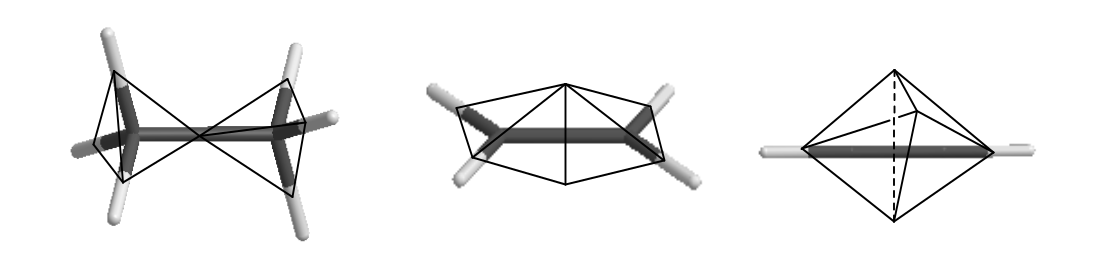
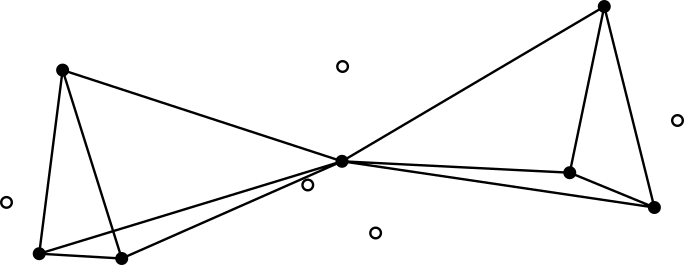
, NO ( ) , CN, C2N2. , O=N-N=O , - , . : , , .
! GAMESS US
$CONTRL SCFTYP=UHF MULT=3
LOCAL = BOYS
RUNTYP=ENERGY NZVAR=0
$END
! PRTLOC = a flag to control supplemental printout. The
! extra output is the rotation matrix to the
! localized orbitals, and, for the Boys method,
! the orbital centroids, for the Ruedenberg
! method, the coulomb and exchange matrices,
! for the population method, atomic populations.
! (default=.FALSE.)
$LOCAL PRTLOC=.T. $END
$SYSTEM TIMLIM=100 MWORDS=5 $END
$BASIS GBASIS=STO NGAUSS=3 $END
$GUESS GUESS=HUCKEL $END
$DATA
Cnv 4
O 8.0 0.0 0.0 0.000
O 8.0 0.0 0.0 1.210
$END
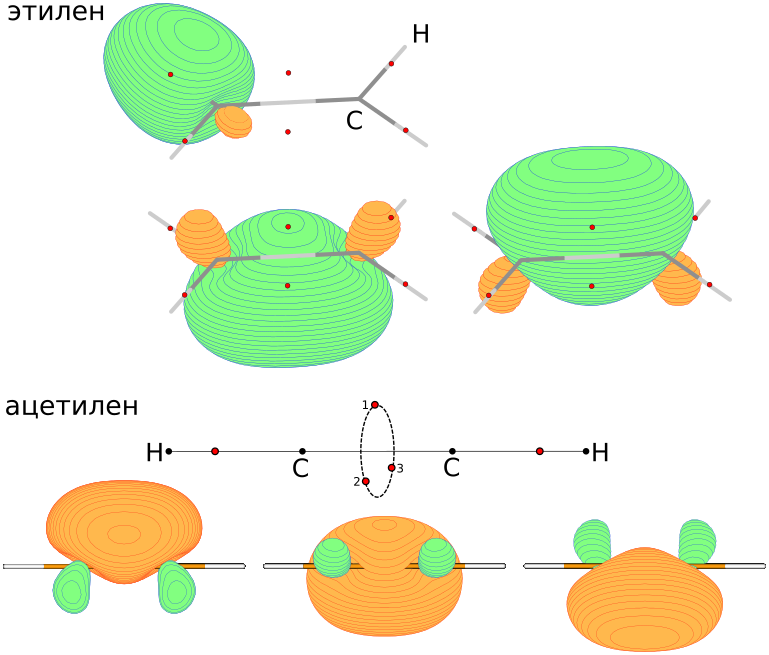
, , "" π- σ-. - , - , , ... , , , , , - .
c :
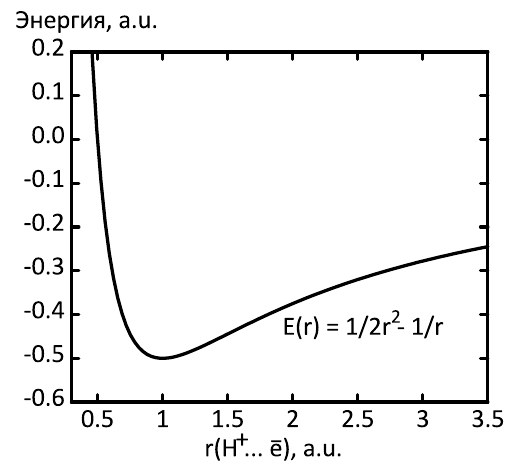
H-H,
,
. :
.

- , MAXIMA , . .
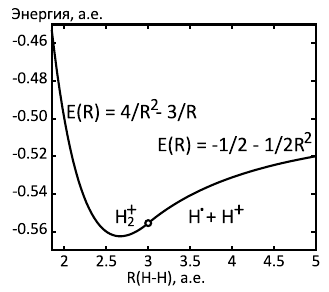
, . 1/16 (164 /), - R=8/3 (1.41 Å). - 255 / , - 1.07 Å. .
. , , . . , , . , , , . , , , .
10% !
