Mutations of a fractal broth called "Multiverse" - about the inflationary model of Andrei Linde and Alan Guth

Abstract: the material describes the problems of the model of a hot Universe, considers the inflationary models of Alan Gut and Andrei Linde, as a result of which a conclusion is made about the feasibility of the hypothesis of the Multiverse, its meaning and self-similarity.

Foreword

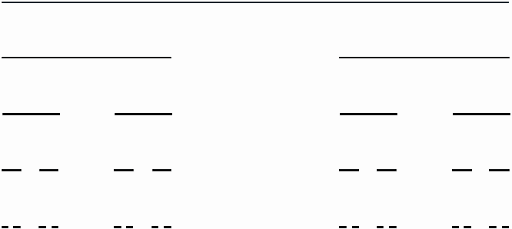
When choosing a topic for this material, I decided that it was time for me to talk with my readers about mathematics, as it was in the article about Fermat's Last Theorem, and on the advice of a professor I know, my eyes fell on fractals. A fractal is a set that has the property of self-similarity. When scaling, any part of a fractal represents the fractal itself. As an example of a fractal, I will cite the Cantor set, which was described in 1883 by Georg Cantor. The set begins with a segment of a certain length, and each subsequent segment is a third of the previous one, and there are two such segments in the "line", and they are separated by a distance of the same segment. No matter how much we scale this set, it will always resemble its original appearance. It looks like this:

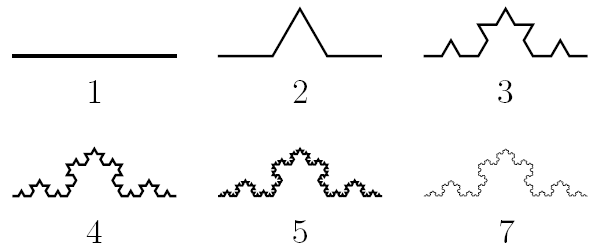
— , . 1904 . (1/3), . , 1/3. , :

, , — . , , . - . , , .

, . . , . — , . , . , , , :

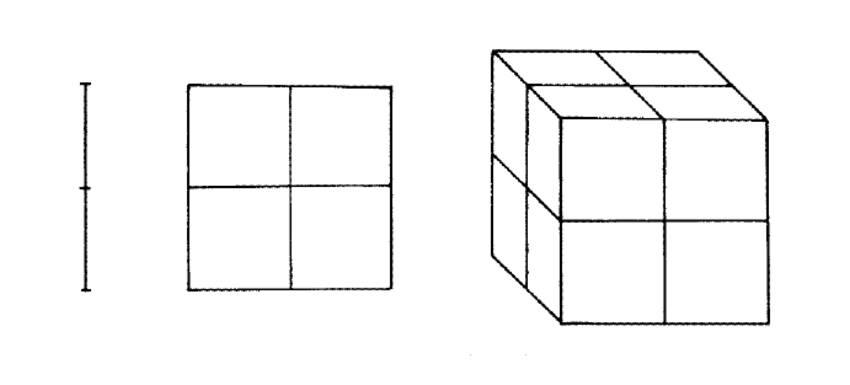
, ; , 3²; , 3³ . , , ? , 4 ! , :

, , 3Blue1Brown, — , , . , 1,3, — 1,05 1,7. :

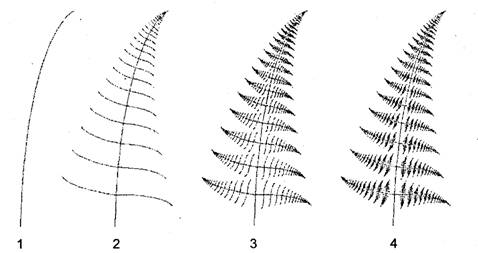
, — , -, 1990- . . , 2,66:

. , , :

, : « », , , .

1981 . . :

«, , ».

, .. , , «Inflationary universe: A possible solution to the horizon and flatness problems», Physical Review 15 1981 . SLAC , - MIT. , :

1. (CMB) , ;

   
   
   
   
   

2. , (.. ).

   
   
   
   
   

? , , . , . : ( 10¹⁶ ). 10^-36 . — . , , . , , , , , ( , .. , , ). — , , (-1ε/3). . -, . , (10^-36 ) , . , .

, , , ( - ). , , . : 10^-35 . , , . .

?

( ) — , . , — , , , , .

, , , , , , — .

? , . :

, .

. , , , , . « » .

()

« , , . . , . , . , , . . , . , , . , ? — ? , ! , , , . - . , — : , , . , , — . , , . , , — , . , — . , . , «» . : — , , , , , — . : . . , , , , ».

?

, , «» , ! , , , , , !

( , ), , t, , . «» - — , , ... . , , — . , -. , , .

, , , — . : - — H2O, : , . , , , — . , , , .

— , , .

«, «-», , , ,   ?   ,   ... ?  :  2000  , . ? 100  , -- (w-) — . ? , . 2 , . 2 , . 100 , . , , -, .

, .     , , , , ,  — ,   , , . , ,  ,   :   ,   , 10   (10¹⁰⁰⁰) ,   , ...   , ,  , - , ,   , ,   .   , , , .  — , . , ,  — , .   , . ».

—

:

• .. « » ;

  
  
  
  
  

• ();

  
  
  
  
  

• ();

  
  
  
  
  

• .. «The Self-Reproducing Inflationary Universe Scientific American» , 1994 ()

  
  
  
  
  

• ()

  
  
  
  
  

• , ()

  
  
  
  
  

• 3Blue1Brown ()

  
  
  
  
  

I also run a telegram channel where you can get acquainted with my activities, pressing issues of cosmology and my old articles ( link ).