For quite a long time I fought with a red-black tree ( hereinafter - kchd ). All the information I found was in the spirit of "the leaves and root of the tree are always black BECAUSE", "top 5 properties of a red-black tree" or "3 cases when balancing and 12 cases when deleting a node". This arrangement did not suit me.
I didn't want to memorize tree properties, pseudocode and balancing options, I wanted to know why. How do colors help balance? Why can't a red node have a red child? Why is the depth of a tree measured "black height"?
I received answers to these questions only when I was given a link to a lecture about two or three trees, with which we will begin.
This article is divided into 3 logical parts. I recommend reading them in the order shown. The first part (this one) will be aimed at an introduction to ccd and acquaintance with it. In the second part, we will talk about balancing and insertion into ccd. In the third and final part, we will analyze the process of deleting a node. Please be patient and enjoy reading :)
Disclaimer
In this article, there will be no information about the pros and cons of the tree, its application, etc.: there is a lot of information about the asymptotics of the tree and working with it on the Internet.
The material is intended for those who are already familiar with ccd and now want to understand them, as well as for those who are just getting to know them.
The article will not contain details of the implementation of the structure.
— . .
-
- , -
, , - - , , , . - - .
- - , . - ( , ). 2-, - 3-. : . :
, .
- , - .
- - , .
, , 5. - 5 .

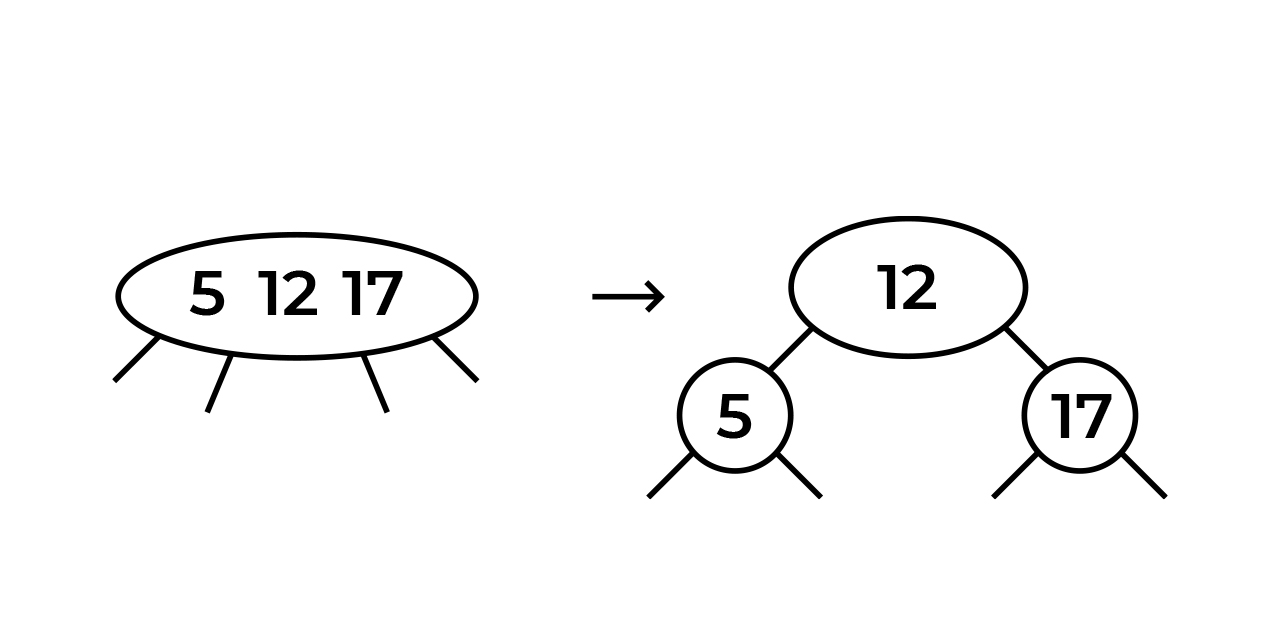
12. 12 (, ), "" ( , ), .. . 5-12.

. 17. . 5-12-17.
- , . ! "" . . 12, 5, - 17.
, , - . : , "" . 3 :
. , ( ).
. ( ).
. , .
.
, . 3. , . , 3 5. 3 5 . 3-5.
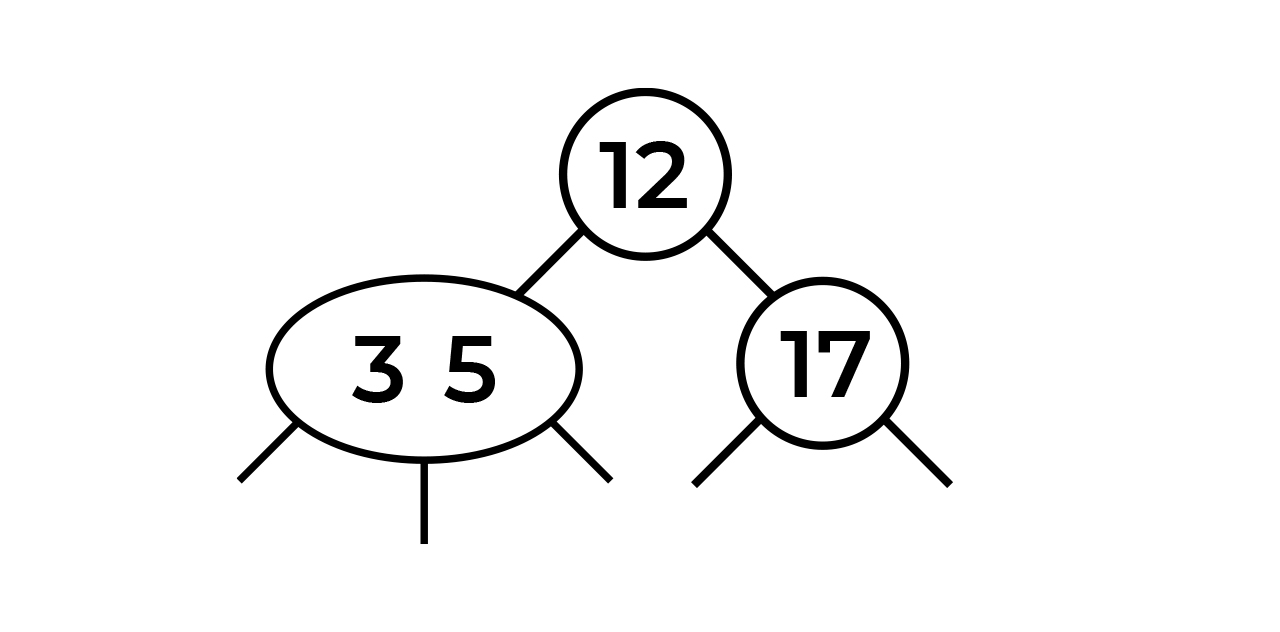
, :)
4 3-5. 3-4-5, , , . ? , .. "" 4 .
. , 4 , - , 4. 5. :
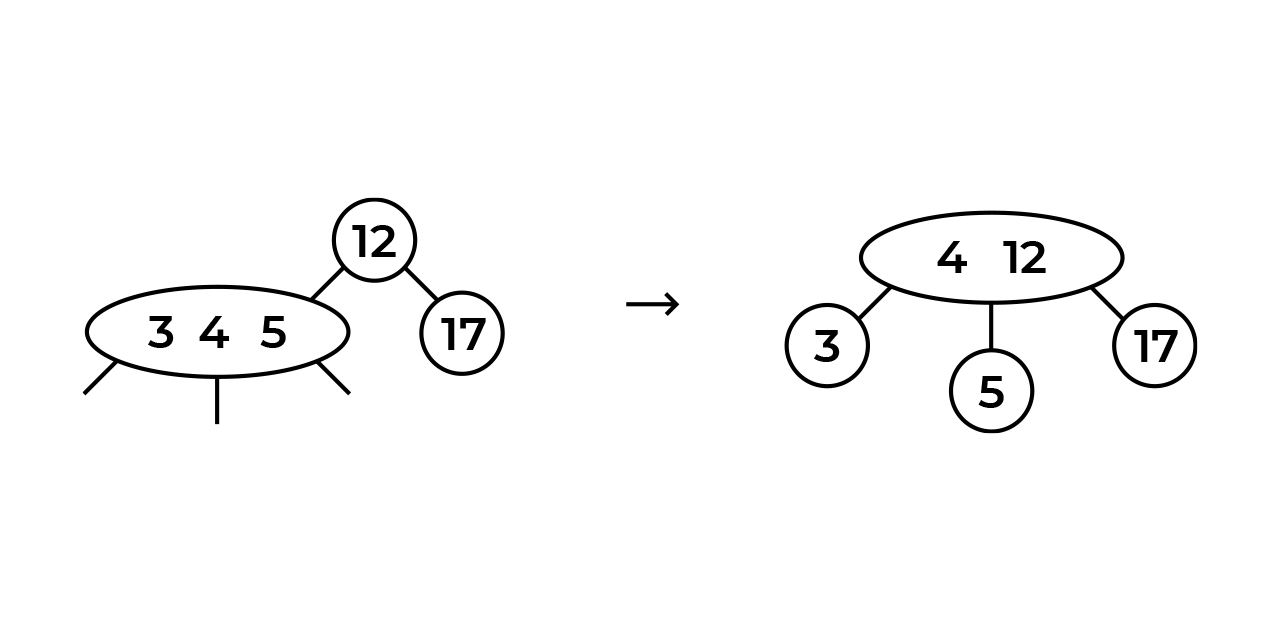
5 ? : - , - . 5 4, 5 , .. . 5 , "", 4-12 (, 5 , "" ).
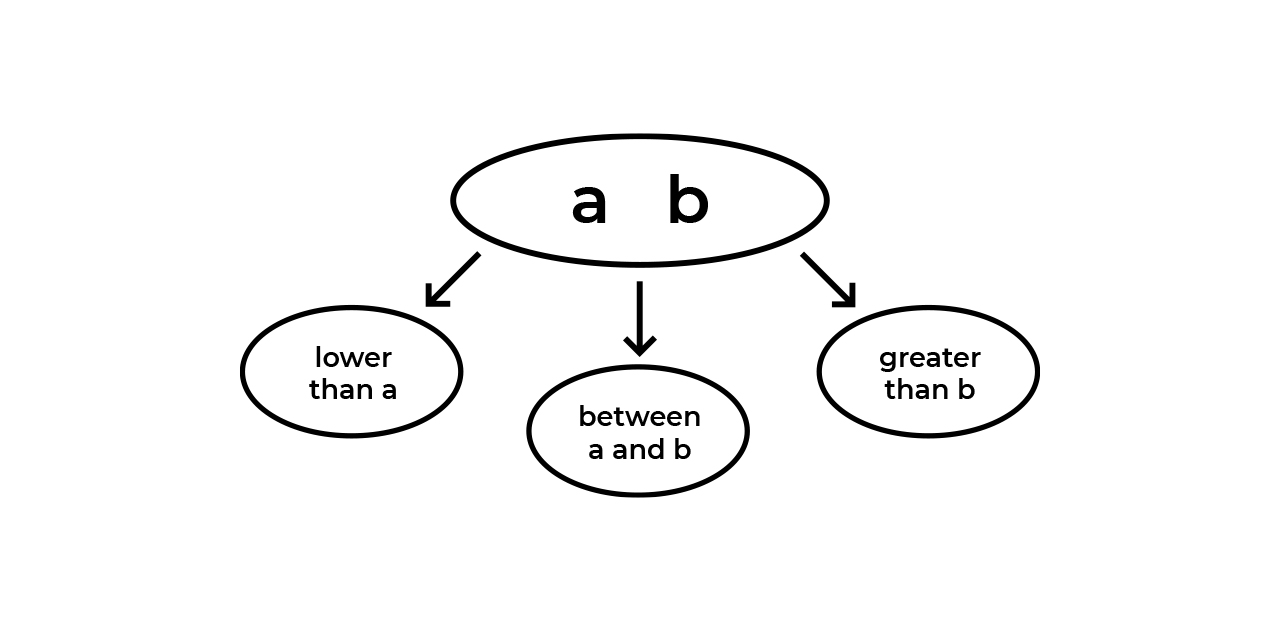
, . :
, , .
, , , .
, , .
, . , , - . , - (, 4-5-12, , 5 4 12). , . , , ( , 7? 9?).
, , , . , , , . .
, , , . , , ( ). - .
-
, - - . - . ?
, 3-. 3- 2- . - , , , ( ), .
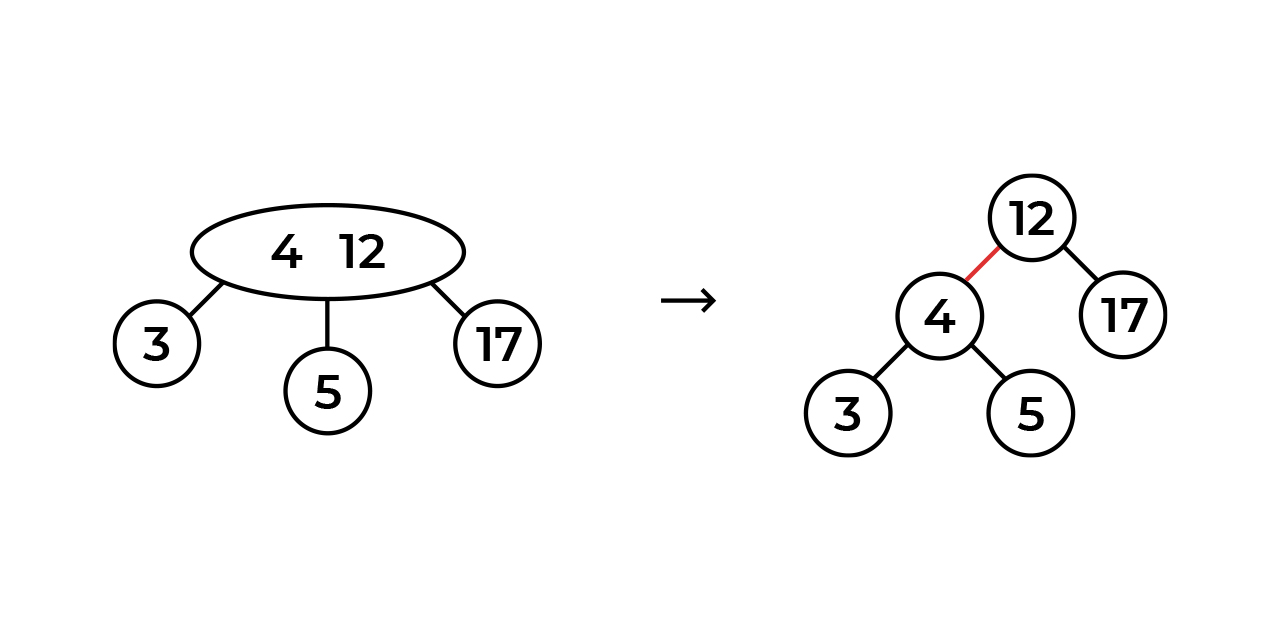
, , .
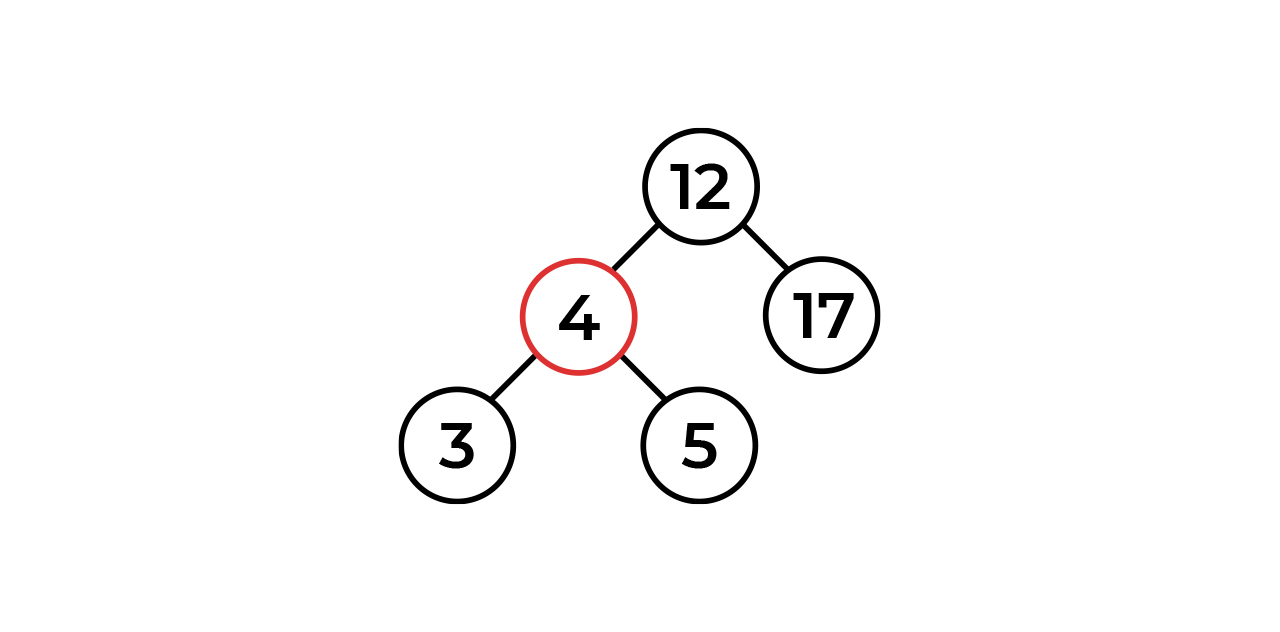
, - . , , ( , ).
-
, - , , 3- ( ). , , . , ( ).
1.
. , , - 3- 2-3 . , 4-, :)
2.
. , : .
3.
null- (, ) - . , . , , .
Since we have touched on null nodes, it should be said that all nodes in the tree should always have two descendants, and if the reference to the descendant is zero, then it leads to the null node. In fact, this raises an implementation question, it was more convenient for me to add a null node (less problems with iterators, balancing, etc.).
Property 4.
The height of the tree is measured only by black nodes and is called the "black height". Here again, everything in general becomes obvious: the red node is only an addition to the black node, it is a part of it, therefore, the height is considered to be based on black nodes.
This concludes the introduction. In the next part, we will talk about how to insert nodes into a tree and balance it.