Content
The main meaning of using the Mahalanobis metric
1. Terms and definitions
2. Mahalanobis distance between two points and between a point and a class
2.1. Theoretical information
2.2. Algorithm for calculating the distance between two points and between a point and a class
2.3. An example of calculating the distance between two points and between a point and a class
3. Mahalanobis distance between two classes
3.1. Theoretical information
3.2. Algorithm for calculating the distance between two classes
3.3. An example of calculating the distance between two classes
4. Mahalanobis distance and k-nearest neighbors method
5. Weighted distance of Mahalanobis
6. Conclusion
If you have any comments or errors, write to quwarm@gmail.com or in the comments.
The main point of using Mahalanobis distance
In Figure 1, two observations are depicted as red dots.
The center of the class is shown as a blue dot.

The question is which observation is closer to the center of the class?
The answer depends on how the distance is measured.
If we measure the distance according to the Euclidean metric , then we get that the distance from the center of the class to the point
is equal to
, to the point
is equal
, that is , the point is
closer to the center of the class.
,
,
« » ,
.
, , .
1.
— , ,
— .
— :
,
—
.
—
:
.
,
—
.
«» - . .
-. - — , .
:
.
, (-) .
2.
( ) ( ) .
2.1
—
, ( )
:
,
, .
, .
, ( 1) ( 0) , .
-.
( [internet archive] ), . .
:
1. : ;
2. : ;
3. : .
: .
, 0, 0 (max(0.0, value)
) NaN, ( sqrt
0.5
) 0 (, ). .
, — .
( ) , — ( ) (. . « »).
, . , .
(, - , . 4) , .
, , * .
*
:
—
,
—
,
—
.
:
— — ( , . «sample covariance»):
—
,
—
.
,
. , ( , . «population covariance»):
:
() ,
;
,
( ),
;
,
( *).
:
.
— :
.
*
—
.
, :
— .
2.
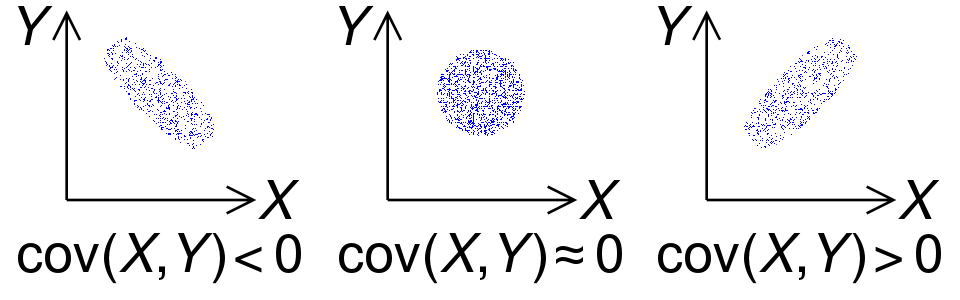
, , ( ), ,
. .
, :
1. - , ,
.
: .
2. (, «perfect covariance»). :
— ;
— .
3.
:
.
1.
, ( — )
.
.
3.
4.
(shrinkage) — (. . ).
,
— ,
— ,
,
.
:
Olivier Ledoit Michael Wolf — ,
—
, ,
— ,
.
, , Python scikit-learn (sklearn.covariance.LedoitWolf, sklearn.covariance.ledoit_wolf, sklearn.covariance.ledoit_wolf_shrinkage).
. 8 , « , , » ( ). — ( ,
, ) , .
.
, ( Python):
— ;
—
:
;
—
:
;
—
:
;
—
:
.
:
—
.
Shrunk Covariance (sklearn.covariance.ShrunkCovariance, sklearn.covariance.shrunk_covariance). , (
).
( Ledoit — Wolf): .
, LedoitWolf ShrunkCovariance ( ) empirical_covariance, (. «population covariance», ).
5.
( ), « »:
— (
/
)
( , «corrected sample standard deviation»):
—
/
)
.
:
,
. , ( , . «uncorrected sample standard deviation»):
- .
, .
, , 10 , . , , , .
2.2
1. .
2. .
3. .
4. , . , .
2.3
(. 3):
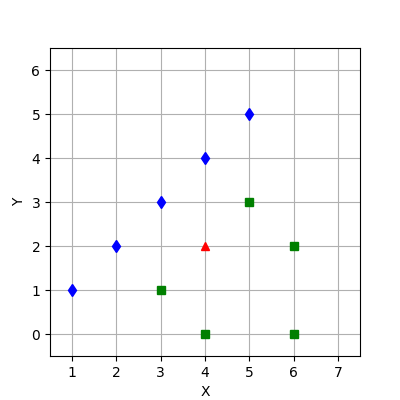
1. .
2. .
:
:
3. .
.
:
: . ,
.
.
:
: . ,
.
Python 3.6 numpy 1.19.5
import numpy as np
classes = [
np.array([[1, 1], [2, 2], [3, 3], [4, 4], [5, 5]]),
np.array([[3, 1], [4, 0], [6, 0], [6, 2], [5, 3]])
]
centroids = [class_.mean(axis=0) for class_ in classes]
standard_deviations = [class_.std(axis=0, ddof=1) for class_ in classes]
covariance_matrices = np.array([np.cov(class_, rowvar=False, ddof=1) for class_ in classes])
det_covariance_matrices = [np.linalg.det(cov) for cov in covariance_matrices]
print("Centroids:", *centroids)
print("Standard deviations:", *standard_deviations)
print("Covariance matrices:", *covariance_matrices.tolist())
print("Determinants of covariance matrices:", det_covariance_matrices)
:
Centroids: [3. 3.] [4.8 1.2] Standard deviations: [1.58113883 1.58113883] [1.30384048 1.30384048] Covariance matrices: [[2.5, 2.5], [2.5, 2.5]] [[1.7, 0.3], [0.3, 1.7]] Determinants of covariance matrices: [0.0, 2.8]
4. , — . , .
, , , .
, .
. — , 5 : (1) — , (2) (LedoitWolf), (3) , (4) , (5) — :
1. — .
Python 3.6 numpy 1.19.5
import numpy as np
def mahalanobis(point_from, point_to, inverse_covariance_matrix):
delta = point_from - point_to
return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5
test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
inverse_covariance_matrix = np.linalg.inv(covariance_matrix + np.identity(covariance_matrix.shape[0]))
print(" :\n", inverse_covariance_matrix, sep='')
for point_to in [class_.mean(axis=0), *class_]:
print("d_E-M (", test_point, ", ", point_to, ", (COV+E)^(-1)) = ",
mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')
:
: [[ 0.58333333 -0.41666667] [-0.41666667 0.58333333]] d_E-M ([4. 2.], [3. 3.], (COV+E)^(-1)) = 1.414213562373095 d_E-M ([4. 2.], [1. 1.], (COV+E)^(-1)) = 1.8257418583505538 d_E-M ([4. 2.], [2. 2.], (COV+E)^(-1)) = 1.5275252316519465 d_E-M ([4. 2.], [3. 3.], (COV+E)^(-1)) = 1.414213562373095 d_E-M ([4. 2.], [4. 4.], (COV+E)^(-1)) = 1.5275252316519465 d_E-M ([4. 2.], [5. 5.], (COV+E)^(-1)) = 1.8257418583505536
— , .
2. (LedoitWolf).
Python 3.6 numpy 1.19.5 scikit-learn 0.24.1
import numpy as np
from sklearn.covariance import LedoitWolf
def mahalanobis(point_from, point_to, inverse_covariance_matrix):
delta = point_from - point_to
return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5
def approx(number, *, sign, epsilon=1e-4):
return number + np.sign(sign) * epsilon
test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
lw = LedoitWolf().fit(class_)
lw_covariance_matrix = lw.covariance_
lw_lambda = lw.shrinkage_
covariance_matrix = np.cov(class_, rowvar=False, ddof=0)
mu = np.sum(np.trace(covariance_matrix)) / class_.shape[0]
T = mu * np.identity(class_.shape[1])
print("T:", *T)
print("COV(*):", *lw_covariance_matrix)
print("Lambda:", lw_lambda)
# - T
# ( : T )
# ddof=0, . . LedoitWolf empirical_covariance (. )
first_condition = (np.linalg.eig(T)[0] > approx(0., sign=+1)).all()
print("All(", np.linalg.eig(T)[0], ") > 0 ? -> ", first_condition, sep='')
# - (0, 1]
second_condition = approx(0., sign=+1) < lw_lambda <= 1
print("Lambda =", lw_lambda, "in (0, 1] ? ->", second_condition)
# - COV(*)
# lambda, T
cov_eig = min(np.linalg.eig(lw_covariance_matrix)[0])
lambda_t_eig = lw_lambda * min(np.linalg.eig(T)[0])
third_condition = cov_eig >= lambda_t_eig
print(cov_eig, ">=", lambda_t_eig, "? ->", third_condition)
conditions = [first_condition, second_condition, third_condition]
if all(conditions):
print(" ")
#
inverse_lw_covariance_matrix = np.linalg.inv(lw_covariance_matrix)
print(" :\n", inverse_lw_covariance_matrix, sep='')
for point_to in [class_.mean(axis=0), *class_]:
print("d_M(*) (", test_point, ", ", point_to, ", COV(*)) = ",
mahalanobis(test_point, point_to, inverse_lw_covariance_matrix), sep='')
else:
print(" (1-3): ", [i for i, x in enumerate(conditions, 1) if not x])
:
T: [0.8 0. ] [0. 0.8] COV(*): [2. 1.44] [1.44 2. ] Lambda: 0.27999999999999997 All([0.8 0.8]) > 0 ? -> True Lambda = 0.27999999999999997 in (0, 1] ? -> True 0.56 >= 0.22399999999999998 ? -> True : [[ 1.03820598 -0.74750831] [-0.74750831 1.03820598]] d_M(*) ([4. 2.], [3. 3.], COV(*)) = 1.889822365046136 d_M(*) ([4. 2.], [1. 1.], COV(*)) = 2.4283759936997833 d_M(*) ([4. 2.], [2. 2.], COV(*)) = 2.037847864848056 d_M(*) ([4. 2.], [3. 3.], COV(*)) = 1.889822365046136 d_M(*) ([4. 2.], [4. 4.], COV(*)) = 2.037847864848056 d_M(*) ([4. 2.], [5. 5.], COV(*)) = 2.4283759936997833
— , .
3. .
. .
, — .
Python 3.6 numpy 1.19.5
import numpy as np
def mahalanobis(point_from, point_to, inverse_covariance_matrix):
delta = point_from - point_to
return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5
test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
# (Singular Value Decomposition, SVD)
#
pseudo_inverse_covariance_matrix = np.linalg.pinv(covariance_matrix)
print(" :\n", pseudo_inverse_covariance_matrix, sep='')
for point_to in [class_.mean(axis=0), *class_]:
print("d_M+ (", test_point, ", ", point_to, ", COV+) = ",
mahalanobis(test_point, point_to, pseudo_inverse_covariance_matrix), sep='')
:
: [[0.1 0.1] [0.1 0.1]] d_M+ ([4. 2.], [3. 3.], COV+) = 0.0 d_M+ ([4. 2.], [1. 1.], COV+) = 1.2649110640673513 d_M+ ([4. 2.], [2. 2.], COV+) = 0.6324555320336757 d_M+ ([4. 2.], [3. 3.], COV+) = 0.0 d_M+ ([4. 2.], [4. 4.], COV+) = 0.6324555320336757 d_M+ ([4. 2.], [5. 5.], COV+) = 1.2649110640673513
— , .
4. .
Python 3.6 numpy 1.19.5
import numpy as np
def euclid_std(point_from, point_to, standard_deviations):
return sum(((point_from - point_to) / standard_deviations) ** 2) ** 0.5
def approx(number, *, sign, epsilon=1e-4):
return number + np.sign(sign) * epsilon
test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
standard_deviations = class_.std(axis=0, ddof=1)
# 0
std_le_0 = standard_deviations <= approx(0., sign=+1, epsilon=1e-6)
print(" :\n", standard_deviations, sep='')
if std_le_0.any():
print(" 0: ", np.where(std_le_0)[0])
else:
for point_to in [class_.mean(axis=0), *class_]:
print("d_std (", test_point, ", ", point_to, ", sigma) = ",
euclid_std(test_point, point_to, standard_deviations), sep='')
:
: [1.58113883 1.58113883] d_std ([4. 2.], [3. 3.], sigma) = 0.8944271909999159 d_std ([4. 2.], [1. 1.], sigma) = 1.9999999999999998 d_std ([4. 2.], [2. 2.], sigma) = 1.2649110640673518 d_std ([4. 2.], [3. 3.], sigma) = 0.8944271909999159 d_std ([4. 2.], [4. 4.], sigma) = 1.2649110640673518 d_std ([4. 2.], [5. 5.], sigma) = 1.9999999999999998
— , .
5. .
Python 3.6 numpy 1.19.5
import numpy as np
def euclid_std(point_from, point_to, standard_deviations):
return sum(((point_from - point_to) / standard_deviations) ** 2) ** 0.5
def euclid_diag(point_from, point_to, standard_deviations):
return euclid_std(point_from, point_to, standard_deviations) \
* (np.prod(standard_deviations ** 2)) ** (1. / point_from.shape[0])
def approx(number, *, sign, epsilon=1e-4):
return number + np.sign(sign) * epsilon
test_point = np.array([4., 2.])
class_ = np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]])
standard_deviations = class_.std(axis=0, ddof=1)
# 0
std_le_0 = standard_deviations <= approx(0., sign=+1, epsilon=1e-6)
print(" :\n", standard_deviations, sep='')
if std_le_0.any():
print(" 0: ", np.where(std_le_0)[0])
else:
for point_to in [class_.mean(axis=0), *class_]:
print("d_diag (", test_point, ", ", point_to, ", sigma) = ",
euclid_diag(test_point, point_to, standard_deviations), sep='')
:
: [1.58113883 1.58113883] d_diag ([4. 2.], [3. 3.], sigma) = 2.2360679774997902 d_diag ([4. 2.], [1. 1.], sigma) = 5.0 d_diag ([4. 2.], [2. 2.], sigma) = 3.16227766016838 d_diag ([4. 2.], [3. 3.], sigma) = 2.2360679774997902 d_diag ([4. 2.], [4. 4.], sigma) = 3.16227766016838 d_diag ([4. 2.], [5. 5.], sigma) = 5.0
— , .
—
,
— .
Python 3.6 numpy 1.19.5
import numpy as np
def mahalanobis(point_from, point_to, inverse_covariance_matrix):
delta = point_from - point_to
return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta)) ** 0.5
def approx(number, *, sign, epsilon=1e-4):
return number + np.sign(sign) * epsilon
test_point = np.array([4., 2.])
class_ = np.array([[3., 1.], [4., 0.], [6., 0.], [6., 2.], [5., 3.]])
covariance_matrix = np.cov(class_, rowvar=False, ddof=1)
if abs(np.linalg.det(covariance_matrix)) <= approx(0., sign=+1):
print(" 0. .")
else:
inverse_covariance_matrix = np.linalg.inv(covariance_matrix)
print(" (d_M):\n", inverse_covariance_matrix, sep='')
for point_to in [class_.mean(axis=0), *class_]:
print("d_M (", test_point, ", ", point_to, ", COV^(-1)) = ",
mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')
covariance_matrix = covariance_matrix + np.identity(class_.shape[1])
inverse_covariance_matrix = np.linalg.inv(covariance_matrix)
print(" (d_E-M):\n", inverse_covariance_matrix, sep='')
for point_to in [class_.mean(axis=0), *class_]:
print("d_E-M (", test_point, ", ", point_to, ", (COV+E)^(-1)) = ",
mahalanobis(test_point, point_to, inverse_covariance_matrix), sep='')
:
(d_M): [[ 0.60714286 -0.10714286] [-0.10714286 0.60714286]] d_M ([4. 2.], [4.8 1.2], COV^(-1)) = 0.9561828874675149 d_M ([4. 2.], [3. 1.], COV^(-1)) = 1.0 d_M ([4. 2.], [4. 0.], COV^(-1)) = 1.5583874449479593 d_M ([4. 2.], [6. 0.], COV^(-1)) = 2.3904572186687876 d_M ([4. 2.], [6. 2.], COV^(-1)) = 1.5583874449479593 d_M ([4. 2.], [5. 3.], COV^(-1)) = 1.0 (d_E-M): [[ 0.375 -0.04166667] [-0.04166667 0.375 ]] d_E-M ([4. 2.], [4.8 1.2], (COV+E)^(-1)) = 0.7302967433402214 d_E-M ([4. 2.], [3. 1.], (COV+E)^(-1)) = 0.8164965809277259 d_E-M ([4. 2.], [4. 0.], (COV+E)^(-1)) = 1.224744871391589 d_E-M ([4. 2.], [6. 0.], (COV+E)^(-1)) = 1.8257418583505536 d_E-M ([4. 2.], [6. 2.], (COV+E)^(-1)) = 1.224744871391589 d_E-M ([4. 2.], [5. 3.], (COV+E)^(-1)) = 0.8164965809277259
— .
•
:
1. — : ;
2. (LedoitWolf): ;
3. : ;
4. : ;
5. : .
( ): .
( — ): .
3, ( ) — , .
•
:
1. — : ;
2. (LedoitWolf): ;
3. : ;
4. : ;
5. : .
( ): .
( — ): .
3, ( ) .
•
:
1. — : ;
2. (LedoitWolf): ;
3. : ;
4. : ;
5. : .
( ): .
( — ): .
3, ( ) — , .
.
3.
( ) .
3.1
—
:
— ,
— ,
— ,
— .
:
.
, , .
, , ( ) (. 2 « »):
- :
— ,
.
3.2
1. .
2. .
3. , .
4. , . , — .
3.3
. 2.2.
.
3 . 2.2.
4 .
4. , . , — .
:
:
•
.
— .
:
— ;
— — .
•
.
—
.
:
—
;
— —
.
•
.
—
.
:
—
;
— —
.
4. k-
- . ,
- ( )
.
- .
:
— : ( — );
— ( , ).
Python 3.6 numpy 1.19.5
#
import heapq
from collections import Counter
from operator import itemgetter
import numpy as np
class MkNN:
def __init__(self, k, classes, inv_cov_matrices):
self.n = len(classes)
self.k = k
self.classes = classes
self.inv_cov_matrices = inv_cov_matrices
@staticmethod
def mahalanobis_sqr(point_from, point_to, inverse_covariance_matrix):
delta = point_from - point_to
return max(np.float64(0), np.dot(np.dot(delta, inverse_covariance_matrix), delta))
def _get_k_smallest(self, test_point):
generator = (
(MkNN.mahalanobis_sqr(test_point, point, inv_cov), i)
for i, (class_, inv_cov) in enumerate(zip(self.classes, self.inv_cov_matrices))
for point in class_
)
return heapq.nsmallest(self.k, generator, key=itemgetter(0))
def predict(self, test_point):
return heapq.nlargest(1, Counter((i for _, i in self._get_k_smallest(test_point))).items(),
key=lambda t: (t[1], -t[0]))[0][0]
def predict_proba(self, test_point):
most_common = Counter((i for _, i in self._get_k_smallest(test_point)))
classes_proba = np.array([most_common.get(i, 0) for i in range(self.n)])
return classes_proba / classes_proba.sum()
def predict_all_max(self, test_point):
p = self.predict_proba(test_point)
return np.where(p == max(p))[0]
def main():
# , - classes
test_points = np.array([[4., 2.]])
#
classes = [
np.array([[1., 1.], [2., 2.], [3., 3.], [4., 4.], [5., 5.]]),
np.array([[3., 1.], [4., 0.], [6., 0.], [6., 2.], [5., 3.]])
]
#
n_train_points = sum(class_.shape[0] for class_ in classes)
#
cov_matrices = [np.cov(class_, rowvar=False, ddof=1) for class_ in classes]
# -- -
inv_cov_matrices = [np.linalg.inv(cov + np.identity(cov.shape[0])) for cov in cov_matrices]
for test_point in test_points:
print("Point:", test_point)
# k 1 ( )
for i in range(1, n_train_points):
classifier = MkNN(i, classes, inv_cov_matrices)
print(f"{i}nn:",
1 + classifier.predict(test_point),
classifier.predict_proba(test_point),
classifier.predict_all_max(test_point))
if __name__ == "__main__":
main()
:
"knn: [ ( 1), ] [ ] [ ( 0), ]".
Point: [4. 2.] 1nn: 2 [0. 1.] [1] 2nn: 2 [0. 1.] [1] 3nn: 2 [0. 1.] [1] 4nn: 2 [0. 1.] [1] 5nn: 2 [0.2 0.8] [1] 6nn: 2 [0.33333333 0.66666667] [1] 7nn: 2 [0.42857143 0.57142857] [1] 8nn: 1 [0.5 0.5] [0 1] 9nn: 2 [0.44444444 0.55555556] [1]
. 4.

Python 3.6
# ...
from operator import sub
import numpy as np # 1.19.5
from matplotlib import colors, pyplot as plt # 3.3.4
#
def show_data_on_mesh(k, classes, inv_cov_matrices):
#
min_ = np.min([np.min(class_, axis=0) for class_ in classes], axis=1) - 1
max_ = np.max([np.max(class_, axis=0) for class_ in classes], axis=1) + 1
min_c = min(min_[0], min_[1])
max_c = max(max_[0], max_[1])
h = 0.05
test_mesh = np.meshgrid(np.arange(min_c, max_c, h), np.arange(min_c, max_c, h))
test_points = np.c_[test_mesh[0].ravel(), test_mesh[1].ravel()]
#
classifier = MkNN(k, classes, inv_cov_matrices)
test_mesh_labels = [sub(*classifier.predict_proba(x)) for x in test_points]
#
plt.figure(figsize=(6, 5), dpi=90)
class_colormap = colors.ListedColormap(['#070648', '#480607'])
plt.pcolormesh(test_mesh[0], test_mesh[1],
np.asarray(test_mesh_labels).reshape(test_mesh[0].shape),
cmap='coolwarm', shading='nearest')
plt.colorbar()
plt.scatter([point[0] for class_ in classes for point in class_],
[point[1] for class_ in classes for point in class_],
c=[-i for i, class_ in enumerate(classes) for _ in class_],
cmap=class_colormap)
plt.axis([min_c, max_c, min_c, max_c])
plt.xlabel("X")
plt.ylabel("Y")
plt.title("k=" + str(k))
plt.show()
# ...
— .
5.
, — , :
( , ) :
— :
6.
, ( ) , - — .
?
1. , .
2. «Metric Learning» (: Aurélien Bellet, Amaury Habrard, Marc Sebban; ).
3. (, k-means: 1, 2, 3).
4. ().
5. ( 1, article 2 , article 3 ).
If you have any comments or errors, write to quwarm@gmail.com or in the comments.