🕘 🍟 👆🏾 Options math or Black-Scholes model 🎣 🍀 📦

The general interest in the Black-Scholes model (hereinafter - BS) is due to the fact that at one time its authors revolutionized the field of assessing the fair value of options and other derivative financial instruments. Later they received the Nobel Prize for their discoveries, and the analytical formula they derived became, perhaps, the most fundamental and well-known in the world of finance.

The BS model is of no less interest from the point of view of low-level mathematical and probabilistic-theoretical analysis. The article discusses in detail the process of substantiating the basic and key principles of the BS model, and also deduces an analytical formula that is used to assess the fair value of options.

Basic concepts

Option - a contract by which the buyer of an option receives the right , but not the obligation, to buy or sell a given asset at a predetermined price, which is called the strike or strike price.

For the purposes of further analysis, such a financial instrument is most accurately represented as a function that describes the option payments at the time of expiration of the contract. For a simpler and more intuitive understanding, we will consider an option of the Call type, the payout function for which is as follows.

where is the price of the underlying asset, the price of the strike.

From a practical point of view, the function assumes that the option buyer will benefit if the price of the underlying asset exceeds the strike price x_s and which coincides with the difference [x-x_s] . Otherwise, the holder of the option will receive a loss equal to the premium paid for purchasing the option contract.

The concept of fair value is clearly illustrated by the fact that at the time of the transaction, neither party should be in an advantageous position. Such an alignment of forces will be possible only if the value of the option is equal to the expected profit on it. In other words, we will be ready to pay for the option exactly as much as we can earn on it (on average).

Based on the foregoing, it becomes logical to study the function C = max (x - x_s; 0) as a random process, depending on the price of the underlying asset and time , since this function will determine the profit received on the option at a particular point in time , and, consequently, its fair value.

Partial BS equation

, , , . , .

, C = max (x - x_s; 0) x (t) . , x (t) , : $dx = xrdt + x \ sigma \ delta W$ *. , .

$dC = \left(\frac{\partial C}{\partial t} + xr\frac{\partial C}{\partial x} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right)dt + x\sigma\frac{\partial C}{\partial x} \delta W \qquad (1)$

, . (1) , . - .

$\Pi = \frac{\partial C}{\partial x} \cdot x - C(x, t) \qquad (2)$

, $\Delta = \frac{\partial C}{\partial x}$ - .

, , $\Delta = const$ - : $d \Pi = \Delta \cdot dx - dC$ . , , *, (1) . :

$d \Pi = \Delta(xrdt + x\sigma \delta W) - \left [ \left(\frac{\partial C}{\partial t} + xr\frac{\partial C}{\partial x} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right)dt + x\sigma\frac{\partial C}{\partial x} \delta W \right ] \qquad (3)$

, $\Delta = \frac{\partial C}{\partial x}$ , $x\sigma\frac{\partial C}{\partial x} \delta W$ :

$d \Pi = - \left [\frac{\partial C}{\partial t} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right]dt \qquad (4)$

, . $\tau$ , $\tau = T-t$ , . , , $\tau$ , . , : $\frac{\partial C}{\partial t } = - \frac{\partial C}{\partial \tau }$ .

B,S - : $d \Pi = \Pi rdt$ , . (4) , $\Pi$ (2) .

$\frac{\partial C}{\partial \tau }dt - \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}dt =\left( \frac{\partial C}{\partial x} \cdot x - C(x, t) \right ) rdt$

, :

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2 x^2}{2} \frac{\partial ^2 C}{\partial x^2} + rx\frac{\partial C}{\partial x } \qquad (5)$

, . , , , .

. $y = \ln x$ . x^2 , .

, , x^2 , :

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + R\frac{\partial C}{\partial y } \qquad (6)$

$R = r - \frac{\sigma^2}{2}$

, $y = \ln x$

$\frac{\partial C}{\partial x} = \frac{\partial C}{\partial y} \cdot \frac{dy}{dx} = \frac{\partial C}{\partial y} \cdot \frac{1}{x}$

, $y = \ln x$

$\frac{\partial ^2 C}{\partial x^2} =\left ( \frac{\partial C}{\partial y} \cdot \frac{dy}{dx}\right )_x '= (\frac{\partial C}{\partial y})_x '\cdot \frac{dy}{dx} + \frac{\partial C}{\partial y} \cdot (\frac{dy}{dx})_x' = \left( (\frac{\partial C}{\partial y})_y' \cdot y'\right ) \cdot y'+ \frac{\partial C}{\partial y} \cdot y'' =$ $= \left( \frac{\partial^2 C}{\partial y^2} \frac{1}{x}\right ) \frac{1}{x} - \frac{\partial C}{\partial y} \frac{1}{x^2} = \frac{1}{x^2}\left ( \frac{\partial^2 C}{\partial y^2} - \frac{\partial C}{\partial y}\right )$

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2 x^2}{2} \cdot \frac{1}{x^2}\left ( \frac{\partial^2 C}{\partial y^2} - \frac{\partial C}{\partial y}\right ) + rx \cdot \frac{1}{x} \frac{\partial C}{\partial y} \Leftrightarrow \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \left( \frac{\partial ^2 C}{\partial y^2} -\frac{\partial C}{\partial y } \right )+ r\frac{\partial C}{\partial y }$

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \left( \frac{\partial ^2 C}{\partial y^2} -\frac{\partial C}{\partial y } \right )+ r\frac{\partial C}{\partial y } \Rightarrow_1 \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} - \frac{\sigma^2}{2} \frac{\partial C}{\partial y } + r\frac{\partial C}{\partial y } \Rightarrow_2$ $\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + (r - \frac{\sigma^2}{2}) \frac{\partial C}{\partial y } \Rightarrow_3 \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + R\frac{\partial C}{\partial y }$

$R = r - \frac{\sigma^2}{2}$

, . : $C(e^y, \tau) = e^{\alpha y + \beta \tau} \cdot U(y, \tau)$ , $\alpha$ $\beta$ , , :

$\frac{\partial U}{\partial \tau } = \frac{\sigma^2}{2} \frac{\partial ^2 U}{\partial y^2} \qquad (7)$

$Ue^{\alpha y + \beta \tau}$

$\left (U e^{\alpha y + \beta \tau} \right )_\tau ' + rUe^{\alpha y + \beta \tau} = \frac{\sigma^2}{2} \left (U e^{\alpha y + \beta \tau} \right )_{yy} '' + R\left (U e^{\alpha y + \beta \tau} \right )_y ' \qquad (*)$

$\tau$

$\left (U e^{\alpha y + \beta \tau} \right )_\tau ' = \frac{\partial U}{\partial \tau} \cdot e^{\alpha y + \beta \tau} + U \cdot \left ( e^{\alpha y + \beta \tau} \right )_\tau ' = \frac{\partial U}{\partial \tau} \cdot e^{\alpha y + \beta \tau} + \beta U \cdot e^{\alpha y + \beta \tau}$

$\left (U e^{\alpha y + \beta \tau} \right )_y ' = \frac{\partial U}{\partial y} \cdot e^{\alpha y + \beta \tau} + U \cdot \left ( e^{\alpha y + \beta \tau} \right )_y ' = \frac{\partial U}{\partial y} \cdot e^{\alpha y + \beta \tau} + \alpha U \cdot e^{\alpha y + \beta \tau}$

$\left( { \frac{\partial U}{\partial y}} \cdot e^{\alpha y + \beta \tau} + \alpha U \cdot e^{\alpha y + \beta \tau} \right)_y '= \left( { \frac{\partial U}{\partial y}} \cdot e^{\alpha y + \beta \tau} \right)_y' + \left (\alpha U \cdot e^{\alpha y + \beta \tau} \right )_y' =$ $\left( { \frac{\partial^2 U}{\partial y^2}}e^{\alpha y + \beta \tau} + \alpha \frac{\partial U}{\partial y} e^{\alpha y + \beta \tau} \right) + \left ( \alpha \frac{\partial U}{\partial y} e^{\alpha y + \beta \tau} + \alpha^2 U e^{\alpha y + \beta \tau}\right ) =$ $e^{\alpha y + \beta \tau} \left( \frac{\partial^2 U}{\partial y^2} + 2\alpha \frac{\partial U}{\partial y} + \alpha^2 U \right)$

$e^{\alpha y + \beta \tau}$

$\frac{\partial U}{\partial \tau} + \beta U + rU = \frac{\sigma^2}{2}\left( \frac{\partial^2 U}{\partial y^2} + 2\alpha \frac{\partial U}{\partial y} + \alpha^2 U \right) + R\left ( \frac{\partial U}{\partial y} + aU \right )$

$\alpha = -\frac{R}{\sigma^2}$ , $\beta = -(r + \frac{R^2}{2 \sigma^2})$ , :

$\frac{\partial U}{\partial \tau} - (r + \frac{1}{2}\frac{R^2}{\sigma^2}) U + rU = \frac{\sigma^2}{2}\left( \frac{\partial^2 U}{\partial y^2} - \frac {2R}{\sigma^2} \frac{\partial U}{\partial y} + \frac{R^2}{\sigma^4} U \right) + R\left ( \frac{\partial U}{\partial y} - \frac{R}{ \sigma^2}U \right )$

$\frac{\partial U}{\partial \tau } = \frac{\sigma^2}{2} \frac{\partial ^2 U}{\partial y^2}$

(7) :

$P(y, \tau, y_0) = \frac{1}{\sigma \sqrt{2 \pi \tau }} \cdot \exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau}) \qquad (8)$

$(P)_\tau '$ , $(P)_{yy} ''$ (7) .

$e^{*} = \exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau})$

$\tau$ :

$\frac{\partial P}{\partial \tau} = \left (\frac{1}{\sigma \sqrt{2 \pi \tau }} \right )_ \tau ' \cdot e^{*} + \frac{1}{\sigma \sqrt{2 \pi \tau }} \cdot \left (\exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau}) \right )_\tau ' =$ $- \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} \cdot e^{*} + \frac{1}{\sigma \sqrt{2\pi \tau}}\cdot e^{*} \cdot \frac{(y-y_0)^2}{2\sigma^2 \tau^2} = e^{*} \left (\frac{(y-y_0)^2}{2 \sigma^3 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} \right )$

$\frac{\partial P}{\partial y} = \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot (e^{*})_y' = - \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot e^{*} \cdot \frac{(y-y_0)}{ \sigma^2 \tau} \Rightarrow$ $\frac{\partial^2 P}{\partial y^2} = \left (- \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot e^{*} \cdot \frac{(y-y_0)}{\sigma^2 \tau} \right )_y' = \left (- \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \cdot \left ( e^{*} \cdot (y-y_0) \right ) \right )_y' =$ $- \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \cdot \left[\left( e^{*} \cdot (-\frac{(y-y_0)}{\sigma^2 \tau}) \cdot (y-y_0) \right ) + e^{*} \cdot 1\right] = e^{*} \cdot \left (\frac{(y-y_0)^2}{\sigma^5 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \right )$

(7) e^* . :

$\frac{(y-y_0)^2}{2 \sigma^3 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} = \frac{\sigma^2}{2}\left (\frac{(y-y_0)^2}{\sigma^5 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \right )$

, u(s) :

$\int_ {-\infty}^{+\infty} u(s) P(y, \tau, s)ds,$

$\tau$ , (7) , - . , (7) :

$U(y, \tau) = \int_{-\infty}^{+\infty} u(s) P(y, \tau, s)ds =\frac{1}{\sigma \sqrt{2 \pi \tau }} \int_{-\infty}^{+\infty} u(s) \cdot \exp \left(-\frac{(y-s)^2}{2\sigma^2 \tau}\right)ds \qquad (9)$

(9) u(s) . , u(y) = U(y;0) . - , $\tau \mapsto 0$ - $\delta (y-s)$ :

$U(y; 0) = \int _{-\infty}^{+\infty}u(s) \delta (y-s)ds = u(y)$

: f(x) [a;b] , g(x) , $c \in[a,b]$ , :

$\int_{a}^{b} f(x)g(x) dx = f(c) \int_{a}^{b}g(x)dx$

$\varepsilon > 0$ .

$\tau \mapsto 0$ "" $\int_{-\infty}^{y- \varepsilon }, \int_{y-\varepsilon }^{+\infty}$ :

$U(y, \tau) \approx \int_{y- \varepsilon}^{y+ \varepsilon} u(s) P(y, \tau, s)ds$

$d \in [y-\varepsilon; y+\varepsilon ]$ ,

$\int_{y- \varepsilon}^{y+ \varepsilon} u(s) P(y, \tau, s)ds = u(d) \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds.$

, $\lim_{\tau \mapsto 0} \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds = 1$ , $u(d) \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds \approx u(d)$ . , $\varepsilon >0$ , $\tau \mapsto 0$ , $d \mapsto y$ . :

$u(y) = U(y;0) = e^{-\alpha y}\cdot C(e^{y}; 0) = e^{-\alpha y} \cdot \max (e^y -x_s;0)$

, $\max (e^y -x_s;0)=0$ $y < \ln x_s$ , (9) :

$U(y, \tau) = \int_{\ln x_s}^{+\infty} (e^s - x_s)\frac{e^{-\alpha s}}{\sigma \sqrt{2 \pi \tau}} \exp\left(-\frac{(y-s)^2}{2 \sigma^2 \tau}\right)ds \qquad (10)$

(10) $U(y;\tau)$ , , $C(e^y, \tau) = e^{\alpha y + \beta \tau} \cdot U(y, \tau)$ . , $U(y, \tau)$ $C(e^y, \tau)$ .

(10) .

, -:

$C = x_0F \left [ \frac{\ln(xe^{r\tau} / x_s)}{\sigma \sqrt{\tau}} + \frac{\sigma \sqrt{\tau}}{2} \right ] - x_se^{-r\tau}F \left [ \frac{\ln(xe^{r\tau} / x_s)}{\sigma \sqrt{\tau}} - \frac{\sigma \sqrt{\tau}}{2} \right ]$

, , $\sigma -$ .

, :

$z = \frac{(s-y)}{ \sigma \sqrt{\tau}}; \qquad s = z\sigma \sqrt{\tau} + y \qquad$ $z(\ln x_s) = \frac{\ln x_s - y}{\sigma \sqrt{\tau}} =: \gamma \text{ - }$ $dz = \left (\frac{(s-y)}{2 \sigma \sqrt{\tau}} \right )' ds \Rightarrow dz = \frac{ds}{\sigma \sqrt{\tau}} \Rightarrow ds = \sigma \sqrt{\tau}dz$

$U(y, \tau) =\int_{\gamma }^{+\infty}\left (e^{(1-\alpha)(\sqrt{\tau} \sigma z + y)} - x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)} \right ) \frac{e^{-\frac{z^2}{2}}}{\sigma \sqrt{2 \pi \tau}} \sqrt{\tau }\sigma dz =$ $\frac{1}{\sqrt{2 \pi }} \int_{\gamma }^{+\infty}\left (e^{(1-\alpha)(\sqrt{\tau} \sigma z + y) -\frac{z^2}{2} } - x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)-\frac{z^2}{2}} \right ) dz$

$U(y, \tau) =\frac{1}{\sqrt{2 \pi }}\left [ \int_{\gamma }^{+\infty}e^{(1-\alpha)(\sqrt{\tau} \sigma z + y)-\frac{z^2}{2}} dz -\int_{\gamma }^{+\infty} x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)-\frac{z^2}{2}} dz \right ]$

, .

, , , , $e^{-\frac{v^2}{2}}$ , .

, $-\infty$ , . , . :

$\ frac {1} {\ sqrt {2 \ pi}} \ int _ {\ gamma} ^ {+ \ infty} e ^ {- \ frac {z ^ 2} {2}} dz = F (- \ gamma) \ qquad (*)$

, , . , , , . :

, $d_1 = - \ left (\ gamma - \ sigma \ sqrt {\ tau} (1- \ alpha) \ right)$ , $d_2 = - \ left (\ gamma + \ alpha \ sigma \ sqrt {\ tau} \ right)$ , *.

, , . , :

$\ gamma = \ frac {\ ln x_s - y} {\ sigma \ sqrt {\ tau}}; \ qquad \ alpha = - \ frac {R} {\ sigma ^ 2}; \ qquad R = r - \ frac {\ sigma ^ 2} {2}; \ qquad y = \ ln x.$

$d_1 = \ frac {\ ln (xe ^ {r \ tau} / x_s)} {\ sigma \ sqrt {\ tau}} + \ frac {\ sigma \ sqrt {\ tau}} {2}; \ qquad d_2 = \ frac {\ ln (xe ^ {r \ tau} / x_s)} {\ sigma \ sqrt {\ tau}} - \ frac {\ sigma \ sqrt {\ tau}} {2}.$

, . $C (e ^ y, \ tau)$ , , $C (e ^ y, \ tau) = e ^ {\ alpha y + \ beta \ tau} \ cdot U (y, \ tau)$ , , ** $e ^ {\ alpha y + \ beta \ tau}$ .

. , $e ^ {\ alpha y + \ beta \ tau} \ cdot e ^ {y (1- \ alpha) + \ frac {1} {2} \ sigma ^ 2 \ tau (1- \ alpha) ^ 2}$ , $e ^ {\ alpha y + \ beta \ tau} \ cdot e ^ {{\ alpha y + a ^ 2 \ sigma ^ 2 \ tau / 2}}$ $e ^ {- r \ tau}$ . , :

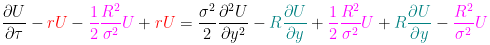
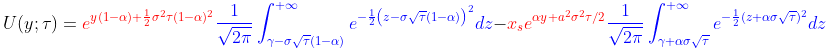
.. " ", 2009 . — 376 .
.. . 2, . 1985 . — 560 .
Wentzel E.S. L.A. Ovcharov Probability theory and its engineering applications. - M., ACADEMA, 2003 .-- 480 p.
Zhulenev S.V. "Financial mathematics. Introduction to classical theory. Part 2.", 2012 - 419 p.
Shiryaev A.N. "Foundations of stochastic financial mathematics. Volume 1. Facts. Models", 1998 - 512 p.

Options math or Black-Scholes model

Basic concepts

Partial BS equation

More articles: