🖨️ 🏢 🚾 How to convert text to algebra: examples 🖐️ 👨‍🎨 👨🏽

In the previous article , the representation of sign sequences by polynomials of matrix units was developed using the example of a linguistic text. The text turns into an algebraic object. With the text, you can perform all the algebraic operations necessary for structuring - calculating headings, dictionaries, annotations, semantic markup. This article provides two examples of the algebraic structuring of texts of a different nature. Morse code was chosen because of the extreme brevity of the dictionary, and mathematical formulas as an example of an inverse problem.

1. Morse-Weil-Gerke code as an algebra of matrix units

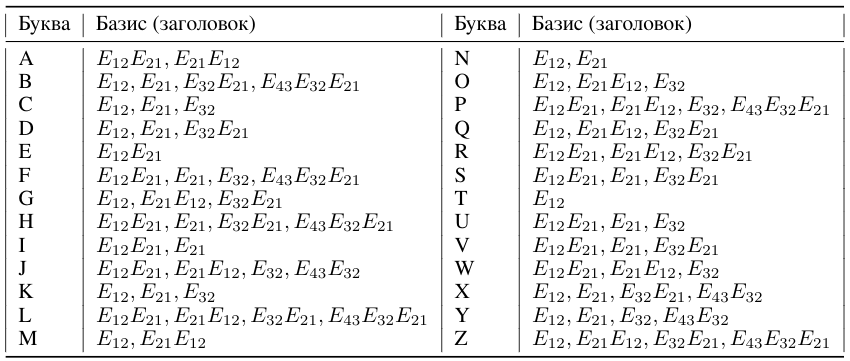
In Morse code, the symbol sequences (texts) of 26 Latin letters consist of dots and dashes. The example was chosen because of the extreme brevity of the dictionary ("dot" and "dash").

The words here are dots or dashes. 26 letters of the alphabet - texts from such words. Each word has two coordinates. The first coordinate is the number of the word (dot or dash) in this letter (from one to four). The second coordinate is the number in the dictionary (1 or 2). Dictionary E ₁₁ ("dot") and E ₂₂ ("dash").

$D_R = E_ {11} + E_ {22}$

Table 1. Morse code: Latin letters as sign sequences (texts)

Each letter (sign sequence) with a number from Table 1 can be associated with a matrix polynomial P of 4x4 matrix units according to formula (8) from article [1] .

Table 2: Morse code: letters as matrix polynomials

For example, the letter Q (No. 17) is associated with a matrix polynomial:

$E_ {12} + E_ {22} + E_ {31} + E_ {42} = \ begin {Vmatrix} 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {Vmatrix}.$

26 - 2 , E₁₂, E_21, E₃₂

26 2 ||P||, , :

$\begin{Vmatrix} a_{11} & \ldots & a_{1n}\\ \ldots & \ldots & \ldots\\ a_{m1} & \ldots & a_{mn} \end{Vmatrix} \begin{Vmatrix} b_{1} \\ \ldots \\ b_{n} \end{Vmatrix}= \begin{Vmatrix} a_{11} \\ \ldots \\ a_{m1} \end{Vmatrix}b_1+\ldots + \begin{Vmatrix} a_{1n} \\ \ldots \\ a_{mn} \end{Vmatrix}b_n,$

2 ||P||₁, ||P||₂, ||P||₃.

$\left\|P\right\|_1=\begin{Vmatrix} E_{12} \\ E_{21} \\ E_{32} \end{Vmatrix}, \left\|P\right\|_2=\begin{Vmatrix} E_{12} \\ E_{21}E_{12} \\ E_{12}+E_{21}E_{12} \\ E_{12}E_{21} \\ E_{21} \\ E_{21}+E_{12}E_{21} \\ E_{32} E_{21} + E_{43}E_{32} E_{21} \\ E_{43}E_{32} E_{21} \\ E_{32} E_{21} \\ E_{32} \\ E_{32} + E_{43}E_{32} \\ E_{43}E_{32} \end{Vmatrix}, \left\|P\right\|_3=\begin{Vmatrix} E_{12}E_{21} \\ E_{12} \\ E_{21} \\ E_{21}E_{12} \\ E_{32}E_{21} \\ E_{32} \\ E_{43}E_{32} E_{21} \\ E_{43}E_{32} \end{Vmatrix}, (1.1)$

||P||₂(||P||₂)^T - - – ( ), , – () - .

(||P||₂)^T||P||₂ - - – , , – – () .

() (1.3). (1.3). 3 4:

: ABCDEFGHIJKLMNOPQRSTUVWXYZ

- ( - E₁₂, E_21, E₃₂) ( ) E₁₂, E_21, E₃₂:

E₁₂ - , «» 4- :

_BCD__G___K_MNO_Q__T___XYZ (13 )

E₂₁ - , «» 4- :

_BCD_F_HI_K__N____S_UV_XY_ (13 )

E₃₂ - , «» 4- :

__C__F___JK ___OP____U_W_Y_ (9)

2.

[1] ( ), . – () ( ), , , . .

V_K, V V:

$V_K=\frac{1}{3}\pi R_1^2H_1, V_{\text{}}=\pi R_2^2H_2, V_T=\pi^2\left(R_3+R_4\right)r,\ \ \ \ \ \ \ \ \ (2.1)$

. , . , R₁² – R₁R₁, πR₁ – , . (1): R₁ H₁ – , R₂ H₂ – , R₃ – , R₄ – , r – , π – π.

. . (2.1) , π. R₁, R₂, R₃, R₄, H₁, H₂ r – . , , ( ), – : R₁=ar, R₂=br, R₃=cr, R₄=dr, H₁=er, H₂=fr . (2.1):

$\begin{gathered} \frac{1}{3}\pi ararer \\ \pi brbrfr \\ \pi \pi \left(c+d \right)rr \end{gathered} \ \ \ \ \ \ \ \ \ \ \ \ (2.2)$

$\begin{gathered} \left(\frac{1}{3}\right)_{1,1}(\pi)_{2,2}(a)_{3,3} (r)_{4,4} (a)_{5,3} (r)_{6,4} (e)_{7,7} (r)_{8,4} \\ (\pi)_{9,2} (b)_{10,10} (r)_{11,4} (b)_{12,10} (r)_{13,4} (f)_{14,14} (r)_{15,4} \\ (\pi)_{16,2} (\pi)_{17,2} \left(c+d \right)_{18,18} (r)_{19,4}(r)_{20,4} \end{gathered} \ \ \ \ \ \ \ \ \ (2.3)$

(2.2)

$P=F_1(P)+F_2(P)+F_3(P), \ \ \ \ \ \ \ \ \ \ (2.4)$

$\begin{gathered} F_1(P) = D_L\left(E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,3}+E_{6,4}+E_{7,7}+E_{8,4}\right)D_R \\ F_2(P) = D_L\left(E_{9,2}+E_{10,10}+E_{11,4}+E_{12,10}+E_{13,4}+E_{14,14}+E_{15,4}\right) D_R \\ F_3(P) = D_L\left(E_{16,2}+E_{17,2}+E_{18,18}+E_{19,4}+E_{20,4}\right) D_R \\ D_R = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{7,7}+E_{10,10}+E_{14,14}+E_{18,18} \\ D_L = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,5}+E_{6,6}+E_{7,7}+ \ldots + E_{20,20} = E \\ D_L=D_R+E_{5,5}+E_{6,6}+E_{5,5}+E_{8,8}+E_{5,5}+E_{9,9} \end{gathered}$

- :

P (2.1) . , , . , «1/3» ( E_1,1), «a» ( E_3,3+E_5,3) , «e» ( E_7,7) ( (2.5)). ( (2.5)) «b» ( E_11,11+E_13,11) «f» ( E_15,15). ( (2.5)) (c+d) ( E_20,20). , (2.5). :

$\begin{gathered} P = P_{\text{}_1}P_{\text{}_1}+P_{\text{}} \\ P = P_{\text{}_2}P_{\text{}_1}+P_{\text{}} \end{gathered}$

$\begin{gathered} P_{\text{}_1} = \left(E_{2,18}+E_{4,12}+E_{6,14}+E_{8,16}\right) +\left(E_{10,18}+E_{12,12}+E_{14,4}+E_{16,16}\right)+\\ +\left(E_{18,18}+E_{19,19}+E_{21,12}+E_{22,14}\right), \\ P_{\text{}_2} = (E_{2,2}+E_{4,4}+E_{6,4}+E_{8,4})+(E_{10,2}+E_{12,4}+E_{14,4}+E_{16,4})+ \\ +(E_{18,2}+E_{19,2}+E_{21,4}+E_{22,4}), \\ P_{\text{}_1} = E_{18,2} + E_{19,2}+E_{12,4} + E_{14,4} + E_{16,4}, \\ P_{\text{}_2} = E_{2,2} + E_{4,4}, \\ P_{\text{}} = E_{1,1}+E_{3,3} + E_{5,3}+E_{7,7}+E_{11,11} + E_{13,11}+E_{15,15}+E_{20,20}.\\ \end{gathered}$

(2.6) P₁ P₂. P₁ (2.1). P₂ D_R (2.1). , (, – , , , ). , , π r^₂, r^₂π.

- (2.6):

$\begin{gathered} P_{\text{}_1}+P_{\text{}} \\ P_{\text{}_2}+P_{\text{}} \end{gathered}$

$\ begin {gathered} P = P _ {\ text {private} _1} \ left (P _ {\ text {div} _1} + P _ {\ text {rest}} \ right) \\ P = P _ {\ text {private } _2} \ left (P _ {\ text {del} _2} + P _ {\ text {rest}} \ right) \ end {gathered}$

P₁ P₂ ( ). . , - P₁ P₂ , .

. . . . . , (2.3) :

P₁ P₂ ( π r ),
P₁ P₂ (),
π r P₁ P₂(1,1,2 3,3,2),
P₁ P₂,
P (, -).

[1] Pshenichnikov S.B. Algebra of text. Researchgate Preprint, 2021

How to convert text to algebra: examples

1. Morse-Weil-Gerke code as an algebra of matrix units

2.

More articles: