
Daniel Lemire - professor at the Correspondence University of Quebec (TÉLUQ), who invented a way to parse double very quickly - together with engineer John Kaiser from Microsoft published another find of theirs: the UTF-8 validator, outperforming the UTF-8 CPP library (2006) at 48..77 times, DFA from Björn Hörmann (2009) - 20..45 times, and Google Fuchsia (2020) - 13..35 times. The news about this publication has already been posted on Habré , but without technical details; so we make up for this shortcoming.
UTF-8 requirements
To begin with, remember that Unicode allows code points from U + 0000 to U + 10FFFF, which are encoded in UTF-8 as sequences of 1 to 4 bytes:
| The number of bytes in the encoding | The number of bits in the code point | Minimum value | Maximum value |
|---|---|---|---|
| one | 1..7 | U + 0000 = 0 0000000 | U + 007F = 0 1111111 |
| 2 | 8..11 | U + 0080 = 110 00010 10 000 000 | U + 07FF = 110 11111 10 111111 |
| 3 | 12..16 | U + 0800 = 1110 0000 10 100000 10 000000 | U + FFFF = 1110 1111 10 111111 10 111111 |
| four | 17..21 | U + 010000 = 11110 000 10 010000 10 000000 10 000000 | U + 10FFFF = 11110 100 10 001111 10 111111 10 111111 |
According to the coding rules, the most significant bits of the first byte of the sequence determine the total number of bytes in the sequence; The most significant zero bit can only be in single-byte (ASCII) characters, the single most significant two bits denote a multibyte character, one and zero - the continuation byte> multibyte character.
What kind of errors could there be in a string encoded this way?
- Incomplete sequence : a leading byte or ASCII character was encountered at the place where a continuation byte was expected;
- Unbuttoned sequence : A leading byte or an ASCII character was expected at the place where a continuation byte was encountered;
- Sequence too long : the leading byte
11111xxx
matches a five-byte or longer sequence that is not allowed in UTF-8; - Going beyond Unicode boundaries : after decoding the four-byte sequence, the code point is higher than U + 10FFFF.
If the line contains none of these four errors, then it can be decoded into a sequence of correct code points. UTF-8, however, requires more - that each sequence of correct code points is encoded uniquely. This adds two more kinds of possible errors:
- : code point ;
- : code points U+D800 U+DFFF UTF-16, code point U+FFFF. UTF-8 , code points , .
In the rarely used CESU-8 encoding, the last requirement is canceled (and in MUTF-8 it is also the penultimate one), due to which the sequence length is limited to three bytes, but the decryption and validation of strings becomes more complicated. For example, the U + 1F600 GRINNING FACE emoticon is represented in UTF-16 as a pair of surrogates
0xD83D 0xDE00
, and CESU-8 / MUTF-8 translates it into a pair of three-byte sequences
0xED 0xA0 0xBD 0xED 0xB8 0x80
; but in UTF-8 this smiley is encoded in one four-byte sequence
0xF0 0x9F 0x98 0x80
.
For each type of error, the following are the bit sequences that lead to it:
| Unfinished sequence | 2nd byte missing | 11xxxxxx 0xxxxxxx
|
11xxxxxx 11xxxxxx
|
||
| Missing 3rd byte | 111xxxxx 10xxxxxx 0xxxxxxx
|
|
111xxxxx 10xxxxxx 11xxxxxx
|
||
| 4th byte missing | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx
|
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx
|
||
| Unbetched sequence | Extra 2nd byte | 0xxxxxxx 10xxxxxx
|
| Extra 3rd byte | 110xxxxx 10xxxxxx 10xxxxxx
|
|
| Extra 4th byte | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
|
| Extra 5th byte | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
|
| Too long sequence | 11111xxx
|
|
| Going beyond Unicode boundaries | U + 110000..U + 13FFFF | 11110100 1001xxxx
|
11110100 101xxxxx
|
||
| ≥ U + 140,000 | 11110101
|
|
1111011x
|
||
| Non-minimal consistency | 2-byte | 1100000x
|
| 3-byte | 11100000 100xxxxx
|
|
| 4-byte | 11110000 1000xxxx
|
|
| Surrogates | 11101101 101xxxxx
|
|
Validating UTF-8
With the naive approach used in the UTF-8 CPP library of Serbian Nemanja Trifunovic, validation is performed in a cascade of nested branches:
const octet_difference_type length = utf8::internal::sequence_length(it);
// Get trail octets and calculate the code point
utf_error err = UTF8_OK;
switch (length) {
case 0:
return INVALID_LEAD;
case 1:
err = utf8::internal::get_sequence_1(it, end, cp);
break;
case 2:
err = utf8::internal::get_sequence_2(it, end, cp);
break;
case 3:
err = utf8::internal::get_sequence_3(it, end, cp);
break;
case 4:
err = utf8::internal::get_sequence_4(it, end, cp);
break;
}
if (err == UTF8_OK) {
// Decoding succeeded. Now, security checks...
if (utf8::internal::is_code_point_valid(cp)) {
if (!utf8::internal::is_overlong_sequence(cp, length)){
// Passed! Return here.
Inside
sequence_length()
and
is_overlong_sequence()
also branching depending on the length of the sequence. If sequences of different lengths are unpredictably interleaved in the input string, then the branch predictor cannot avoid flushing the pipeline several times on each processed character.
A more efficient approach to UTF-8 validation is to use a state machine of 9 states: (the error state is not shown in the diagram)
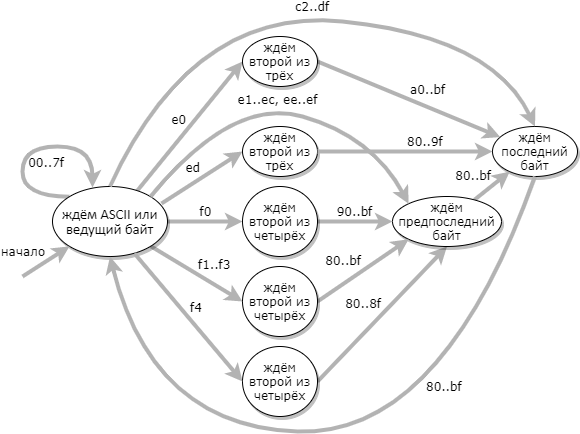
When the automaton transition table is constructed, the validator code is very simple:
uint32_t type = utf8d[byte];
*codep = (*state != UTF8_ACCEPT) ?
(byte & 0x3fu) | (*codep << 6) :
(0xff >> type) & (byte);
*state = utf8d[256 + *state + type];
Here, for each processed character, the same actions are repeated, without conditional transitions - therefore, no pipe resets are required; on the other hand, at each iteration, additional memory access (to the jump table
utf8d
) is performed in addition to reading the input character.
Lemir and Kaiser took the same DFA as the basis for their validator, and achieved acceleration tenfold due to the application of three improvements:
- The jump table was reduced from 364 bytes to 48, so that it fits entirely in three vector registers (128 bits each), and memory accesses are required only for reading the input characters;
- Blocks of 16 adjacent bytes are processed in parallel;
- If a 16-byte block consists entirely of ASCII characters, then it is known to be correct, and there is no need for a more thorough check. This "slice of the path" speeds up the processing of "realistic" texts containing whole sentences in the Latin alphabet two to three times; but on random texts, where the Latin alphabet, hieroglyphs and emoticons are evenly mixed, this does not accelerate.
There are subtle subtleties in the implementation of each of these improvements, so they are worth considering in detail.
Reducing the jump table
The first improvement is based on the observation that to detect most errors (12 invalid bit sequences out of the 19 listed in the table above), it is sufficient to check the first 12 bits of the sequence:
| Unfinished sequence | 2nd byte missing | 11xxxxxx 0xxxxxxx
|
0x02
|
11xxxxxx 11xxxxxx
|
|||
| Unbetched sequence | Extra 2nd byte | 0xxxxxxx 10xxxxxx
|
0x01
|
| Too long sequence | 11111xxx 1000xxxx
|
0x20
|
|
11111xxx 1001xxxx
|
0x40
|
||
11111xxx 101xxxxx
|
|||
| Going beyond Unicode boundaries | U + 1 [1235679ABDEF] xxxx | 111101xx 1001xxxx
|
|
111101xx 101xxxxx
|
|||
| U + 1 [48C] xxxx | 11110101 1000xxxx
|
0x20
|
|
1111011x 1000xxxx
|
|||
| Non-minimal consistency | 2-byte | 1100000x
|
0x04
|
| 3-byte | 11100000 100xxxxx
|
0x10
|
|
| 4-byte | 11110000 1000xxxx
|
0x20
|
|
| Surrogates | 11101101 101xxxxx
|
0x08
|
|
For each of these possible errors, the researchers assigned one of seven bits, as shown in the rightmost column. (The assigned bits are different between their published article and their GitHub code ; here are the values from the article.) To get by with seven bits, the two unicode out-of-bounds subcases had to be repartitioned so that the second concatenated with a 4-byte non-minimal sequence; and the overly long sequence case is split into three subcases and combined with the Unicode out-of-bounds subcases.
Thus, the following changes were made with the Hörmann DKA:
- The input comes not by byte, but by tetrad (nibble);
- The automaton is used as non - deterministic - processing of each tetrad transfers the automaton between subsets of all possible states;
- Eight correct states are combined into one, but one erroneous is divided into seven;
- Three adjacent tetrads are processed not sequentially, but independently of each other, and the result is obtained as the intersection of three sets of final states.
Thanks to these changes, three tables of 16 bytes are sufficient to describe all possible transitions: each element of the table is used as a bit field listing all possible final states. Three of these elements are ANDed together, and if there are non-zero bits in the result, then an error has been detected.
| Tetrad | Value | Possible mistakes | The code |
|---|---|---|---|
| Most significant in the first byte | 0-7 | 2- | 0x01
|
| 8–11 | () | 0x00
|
|
| 12 | 2- ; 2- | 0x06
|
|
| 13 | 2- | 0x02
|
|
| 14 | 2- ; 2- ; | 0x0E
|
|
| 15 | 2- ; ; Unicode; 4- | 0x62
|
|
| 0 | 2- ; 2- ; | 0x37
|
|
| 1 | 2- ; 2- ; 2- | 0x07
|
|
| 2–3 | 2- ; 2- | 0x03
|
|
| 4 | 2- ; 2- ; Unicode | 0x43
|
|
| 5–7 | 0x63
|
||
| 8–10, 12–15 | 2- ; 2- ; | ||
| 11 | 2- ; 2- ; ; | 0x6B
|
|
| 0–7, 12–15 | The 2nd byte is missing; too long sequence; 2-byte non-minimal sequence | 0x06
|
|
| 8 | Extra 2nd byte; too long sequence; going beyond Unicode boundaries; non-minimal consistency | 0x35
|
|
| nine | 0x55
|
||
| 10-11 | Extra 2nd byte; too long sequence; going beyond Unicode boundaries; 2-byte non-minimal sequence; surrogates | 0x4D
|
There are 7 more invalid bit sequences left unprocessed:
| Unfinished sequence | Missing 3rd byte | 111xxxxx 10xxxxxx 0xxxxxxx
|
111xxxxx 10xxxxxx 11xxxxxx
|
||
| 4th byte missing | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx
|
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx
|
||
| Unbetched sequence | Extra 3rd byte | 110xxxxx 10xxxxxx 10xxxxxx
|
| Extra 4th byte | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
|
| Extra 5th byte | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
And here the most significant bit comes in handy, prudently left unused in the transition tables: it will correspond to a sequence of bits
10xxxxxx 10xxxxxx
, i.e. two consecutive bytes. Now checking three notebooks can either detect an error, or give a result
0x00
or
0x80
. And this result of the first check - together with the first notebook - is enough for us:
| Missing 3rd byte | 111xxxxx 10xxxxxx 0xxxxxxx
|
|
111xxxxx 10xxxxxx 11xxxxxx
|
||
| 4th byte missing | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx
|
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx
|
||
| Extra 3rd byte | 110xxxxx 10xxxxxx 10xxxxxx
|
|
| Extra 4th byte | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
|
| Extra 5th byte | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
|
|
| Allowed combinations |
|
|
|
||
This means that to complete the check, it is enough to make sure that each result
0x80
corresponds to one of the two valid combinations.
Vectorization
How to process blocks of 16 adjacent bytes in parallel? The central idea is to use the instruction
pshufb
as 16 concurrent substitutions according to a 16-byte table. For the second check, you need to find in the block all bytes of the form
111xxxxx
and
1111xxxx
; since there is no unsigned vector comparison on Intel, it is replaced by saturation subtraction (
psubusb
).
The simdjson sources are hard to read due to the fact that all the code is split into one-line functions. The entire validator pseudocode looks something like this:
prev = vector(0)
while !input_exhausted:
input = vector(...)
prev1 = prev<<120 | input>>8
prev2 = prev<<112 | input>>16
prev3 = prev<<104 | input>>24
#
nibble1 = prev1.shr(4).lookup(table1)
nibble2 = prev1.and(15).lookup(table2)
nibble3 = input.shr(4).lookup(table3)
result1 = nibble1 & nibble2 & nibble3
#
test1 = prev2.saturating_sub(0xDF) # 111xxxxx => >0
test2 = prev3.saturating_sub(0xEF) # 1111xxxx => >0
result2 = (test1 | test2).gt(0) & vector(0x80)
# result1 0x80 , result2,
#
if result1 != result2:
return false
prev = input
return true
If an incorrect sequence is located at the right edge of the very last block, then it will not be detected by this code. In order not to bother, you can supplement the input string with zero bytes so that at the end you get one completely zero block. Instead, simdjson chose to implement a special check for the last bytes: for the string to be correct, the very last byte must be strictly less
0xC0
, the penultimate byte strictly less
0xE0
, and the third from the end strictly less
0xF0
.
The last of the enhancements Lemierre and Kaiser have come up with is the ASCII cut-off. Determining that there are only ASCII characters in the current block is very simple:
input & vector(0x80) == vector(0)
... In this case, it is enough to make sure that there are no incorrect sequences on the boundary
prev
and
input
, - and you can go to the next block. This check is carried out in the same way as at the end of the input string; the unsigned vector comparison with
[..., 0x0, 0xE0, 0xC0]
, which is not available on Intel, is replaced by the calculation of the vector maximum (
pmaxub
) and its comparison with the same vector.
Checking for ASCII turns out to be the only branch inside the iteration of the validator, and to successfully predict this branch, it is enough that the input string does not interleave entirely ASCII blocks with blocks containing non-ASCII characters. The researchers found that even better results on real texts can be achieved by checking the OR concatenation of four adjacent blocks for ASCII, and skipping all four blocks in the case of ASCII. Indeed, it can be expected that if the author of the text, in principle, uses non-ASCII characters, then they will occur at least once every 64 characters, which is enough to predict the transition.
