History
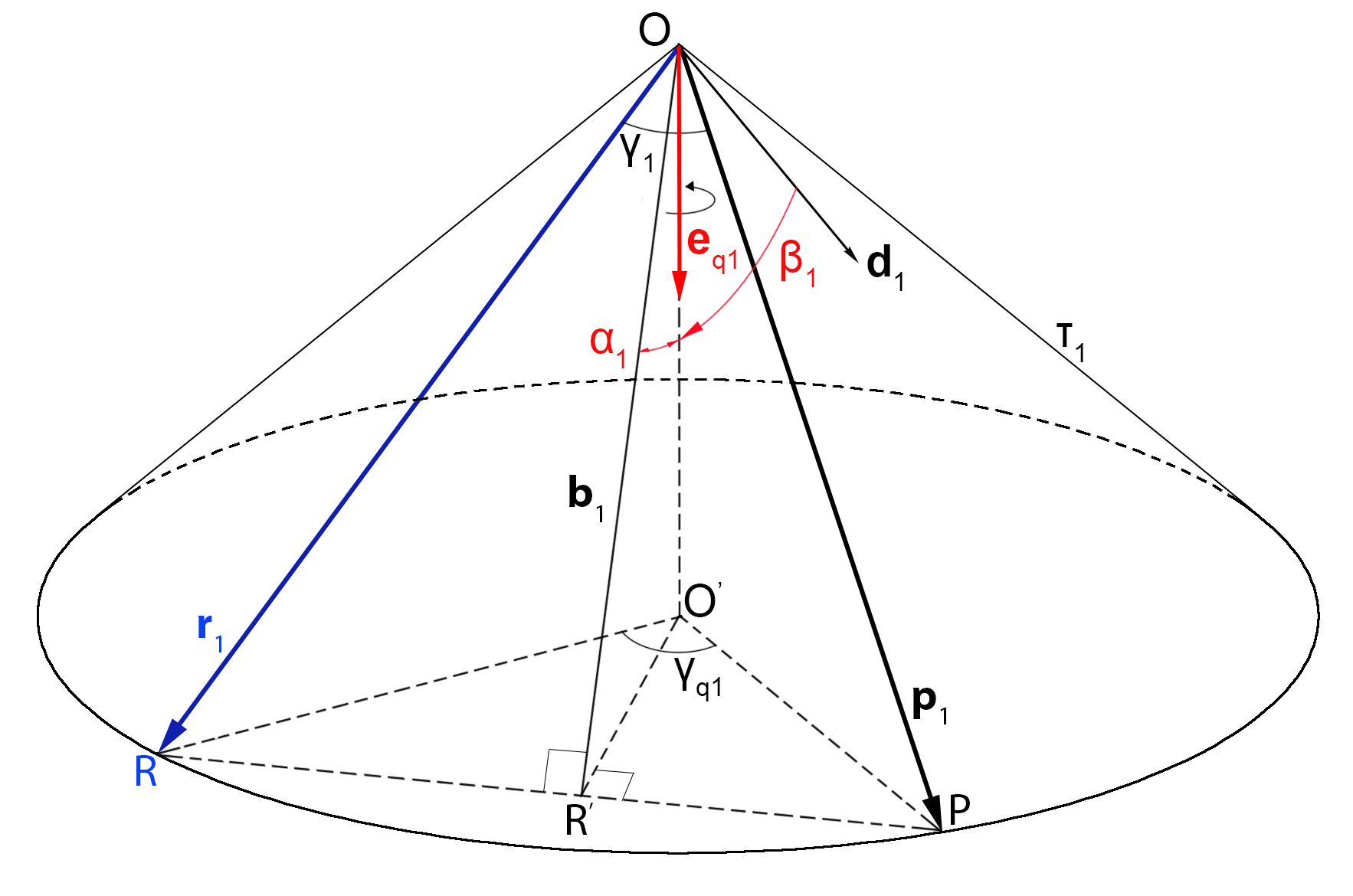
Some time ago I was engaged in an interesting problem related to satellite navigation. Using the phase edge of the signal, the navigation object (NVO) measures the coordinates of navigation satellites (NS) in its coordinate system (local system, LSK). Also, the ONV receives the values of the positions of the NS in the global coordinate system (GCS), and measures the time of receiving the signal of the NS (Fig. 1). It was required to calculate the coordinates of the ONV in the GSK and the system time, that is, to solve the navigation problem.
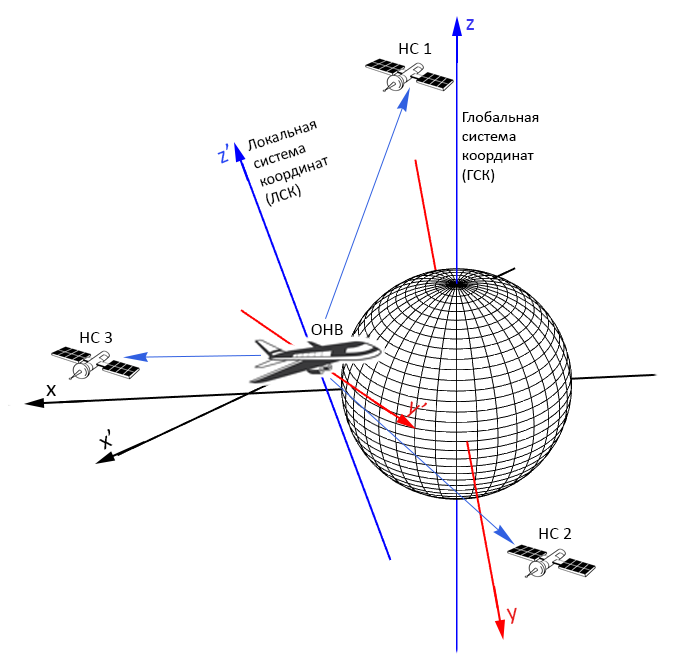
The problem was interesting in that its solution theoretically makes it possible to reduce the number of NNs in comparison with how many NNs are required in the methods implemented in satellite navigation systems. At that time, I mainly paid my attention to the study of the quality of measurements of the phase front and obtaining navigation equations for coordinates and time, assuming that the calculation of the orientation and coordinates of the NVG would not cause any special problems. Moreover, on a plane the problem was solved quickly and easily.
, , , . , . - , .
, , . , . , , , .
, :
: -
- ,
: ,
: -
- ;
; , : 3-
; . , - , , .
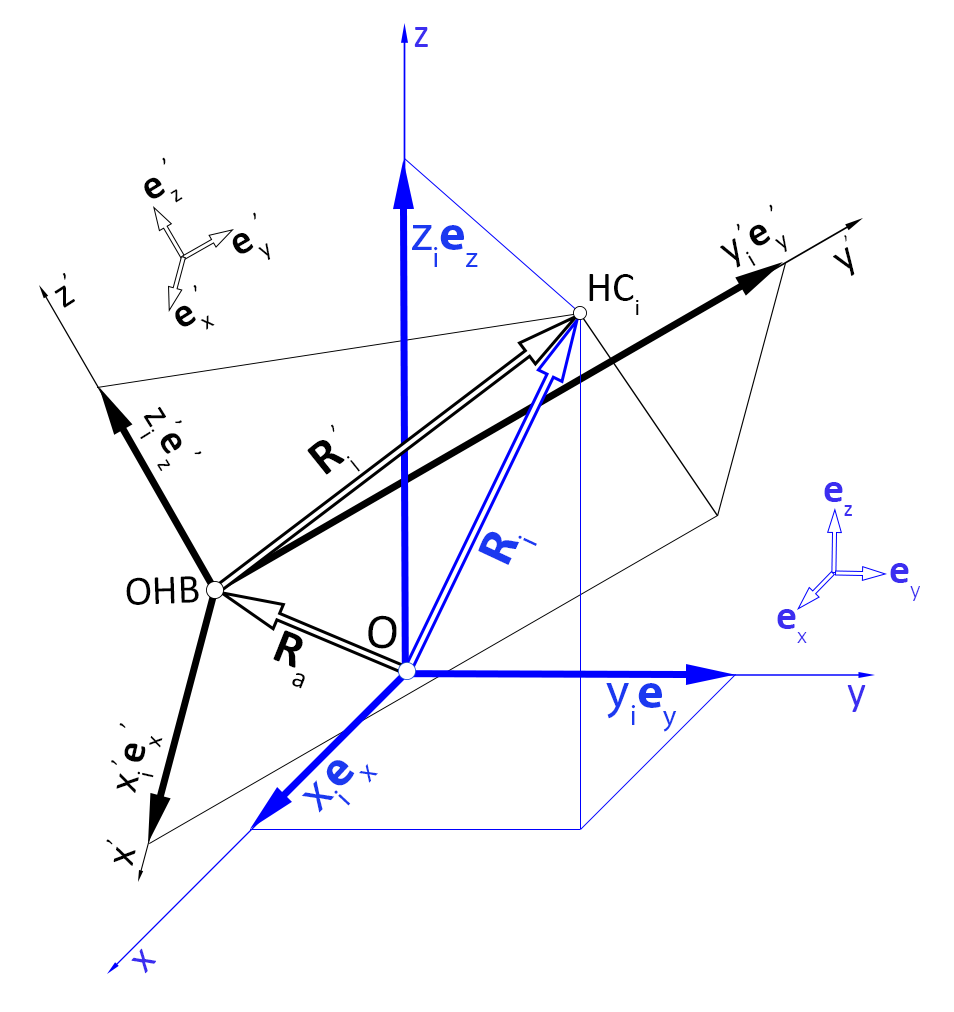
:
: - ,
: , " " (. 2)
.
:
,
- .
,
- ,
.
, ,
,
. ,
. ,
( " "), ,
, . .
:
(1)
(1)
, .
,
. (1) (2) ,
:
.
- (3) (1), . , (3) (2), .
, .
, , (3) (4) . , .
, , , .
, , ,
,
,
,
,
- ( ),
- ; 1, i, j, k - :
(), , . , ,
, ,
,
,
,
. , - .
,
,
,
:
.
,
,
,
,
. "
", , ,
(5).
. :
: ,
: ,
: .
.
. , . k = 1 , i = 2.
-, , , .
-, . , , (3) .
, -, . ,
- ,
, (3) ,
.
T (3) ,
:
:
(3) :
- ,
, (1) :
,
.
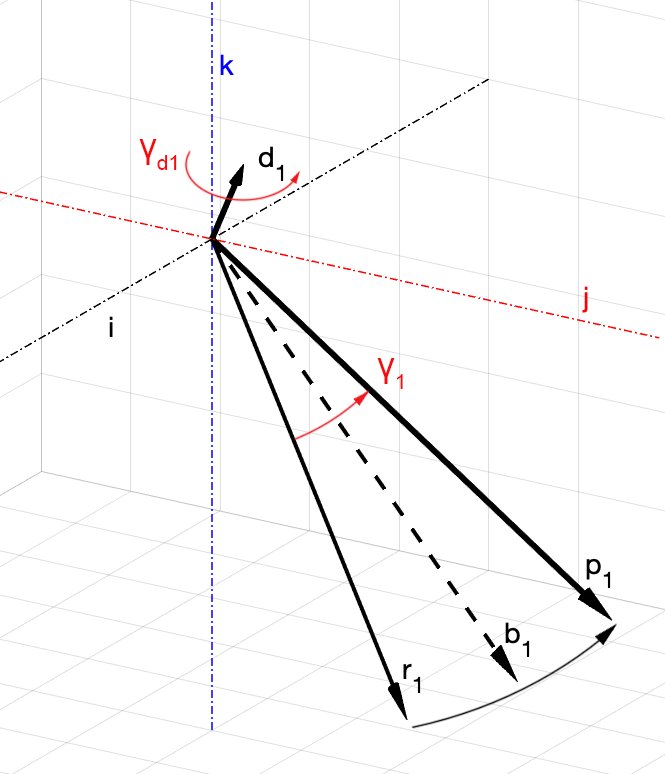
, , ,
, (
). ,
(. 3), ,
.
(6), (3), - : , (6). , , ,
. . 3 ,
,
. ,
.
. 4, ) ) ,
. , ,
, (
),
,
,
,
.
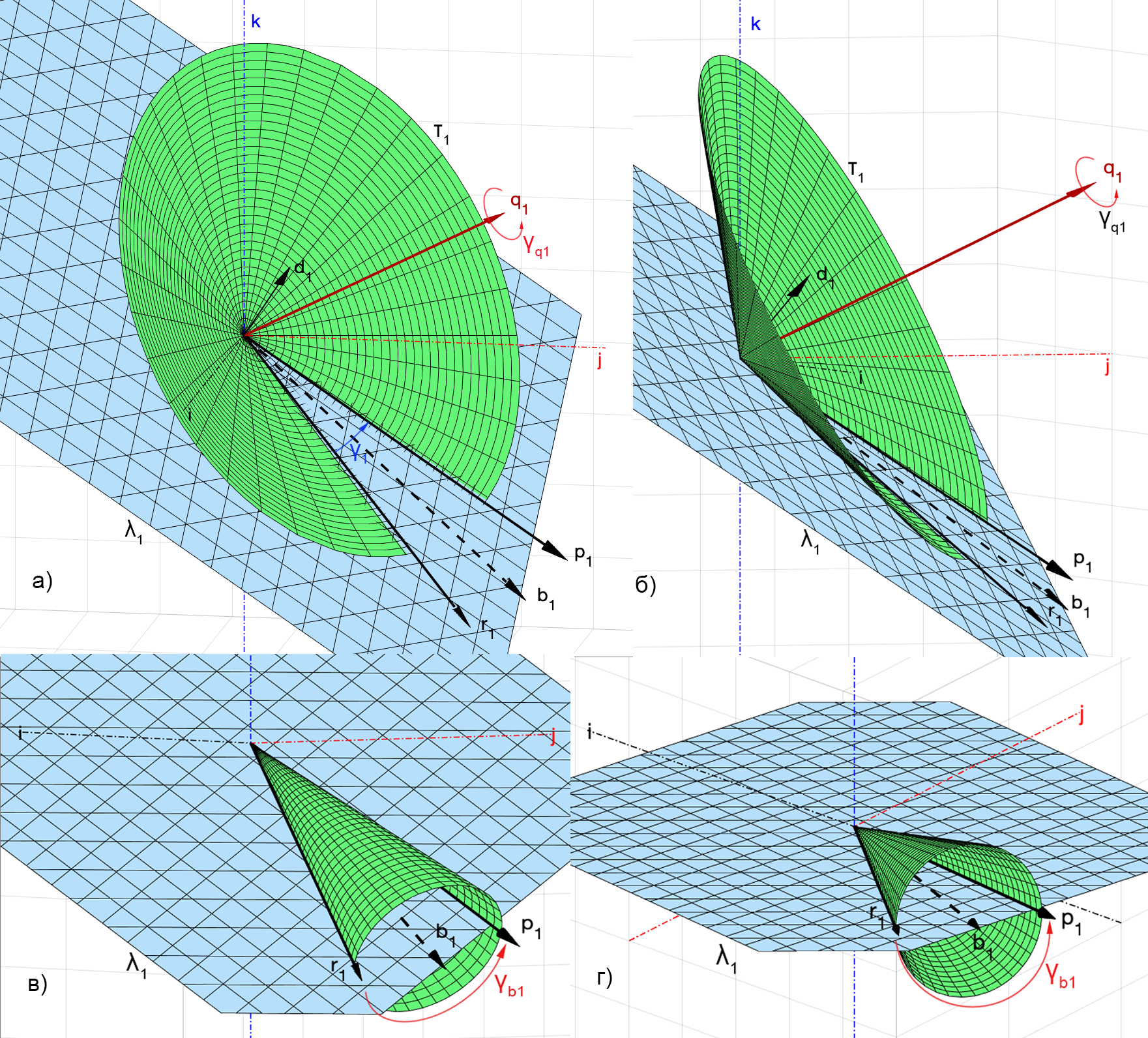
,
,
. (6), (4),
, , (8), , , . , (7)
- .
(8), - , , - .
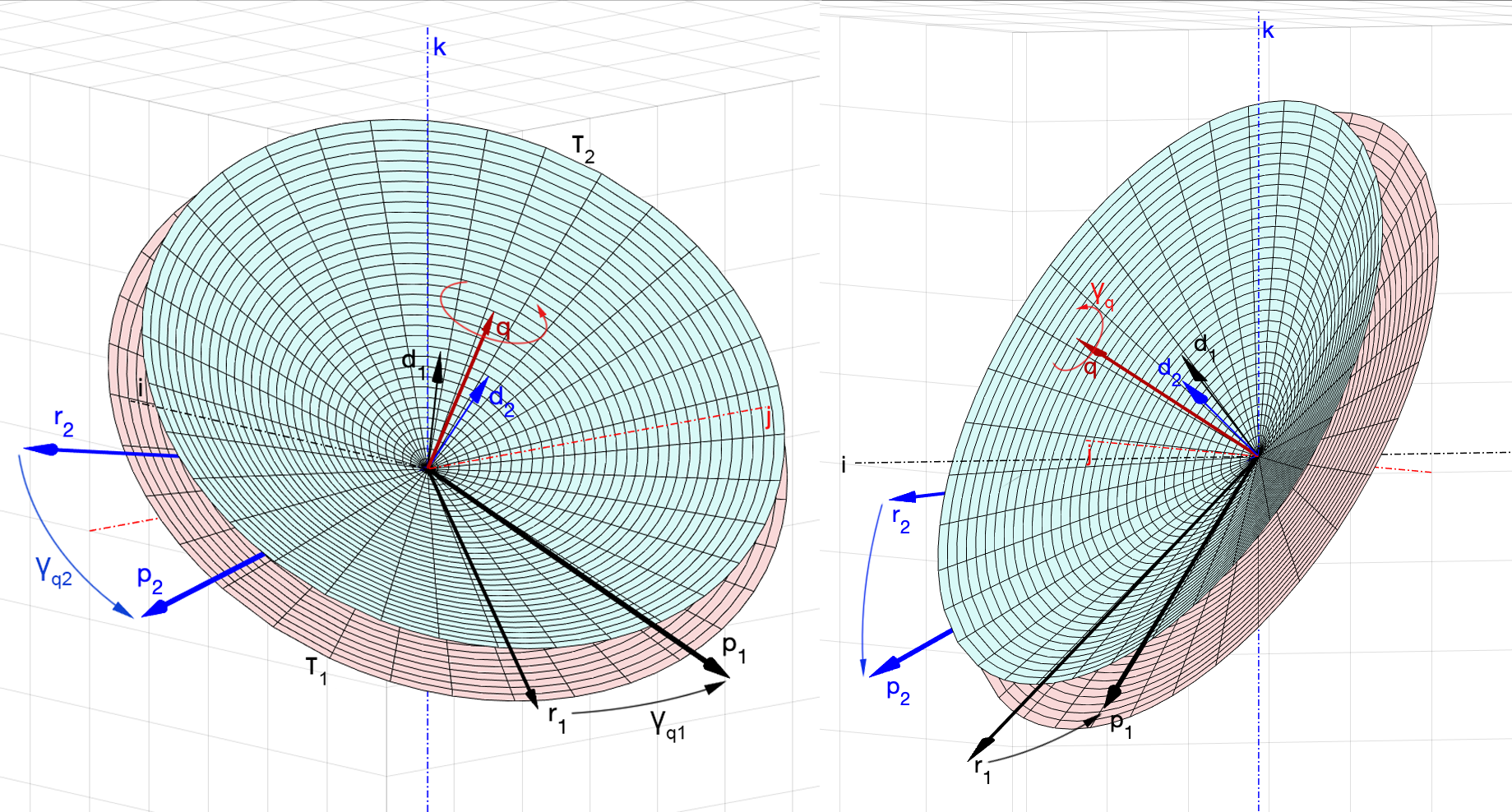
. , ,
,
. ,
(
)
(
),
,
. ,
.
, i = 1, 2, ,
,
,
(. 5).
.
1. ,
,
(. 4, ), )).
2. ,
, i = 1, 2, , ,
(
), . 6). .
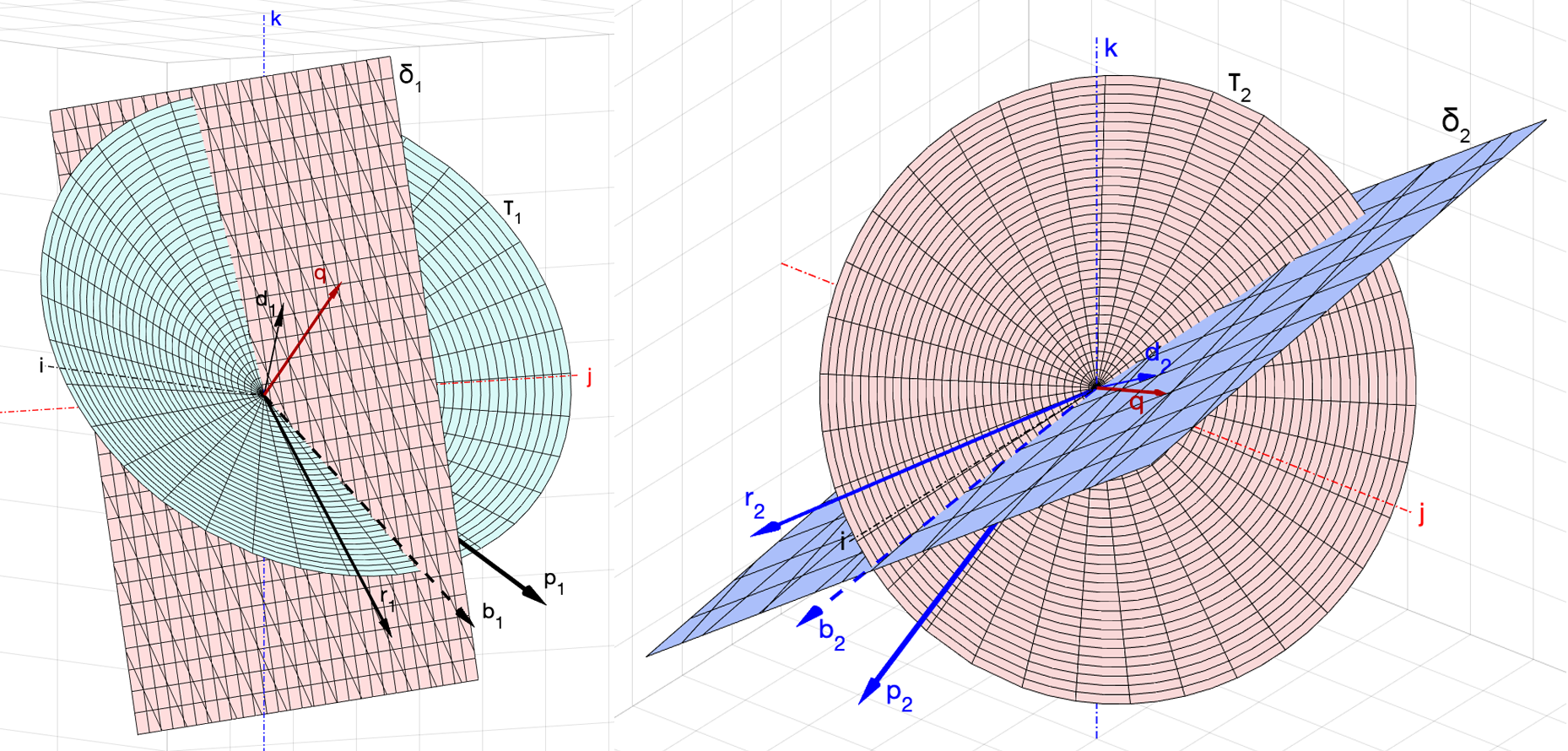
, ,
(
),
.
, , ,
, i = 1, 2,
, .
(. 7).
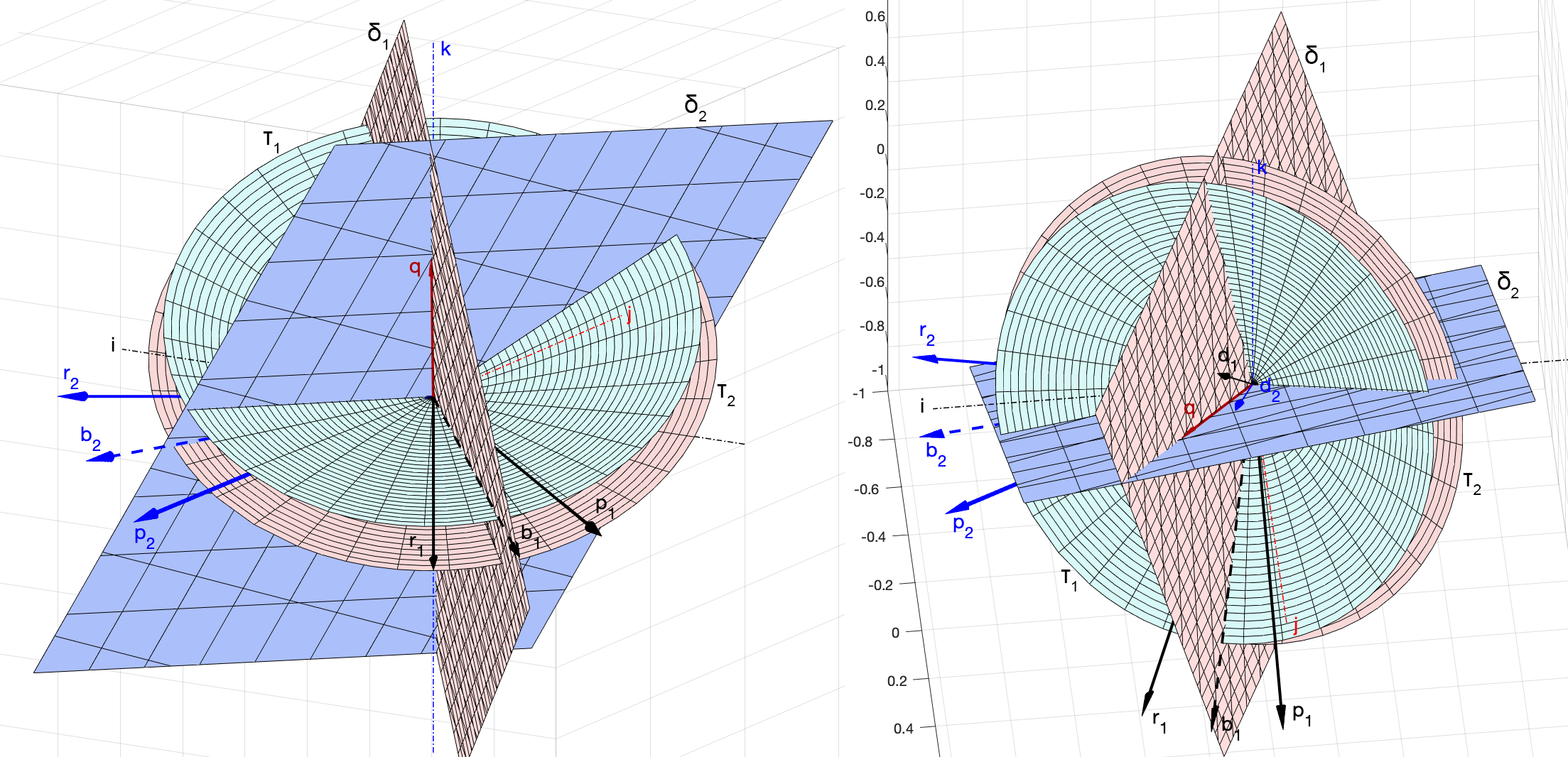
, . ,
,
(. 8).
.
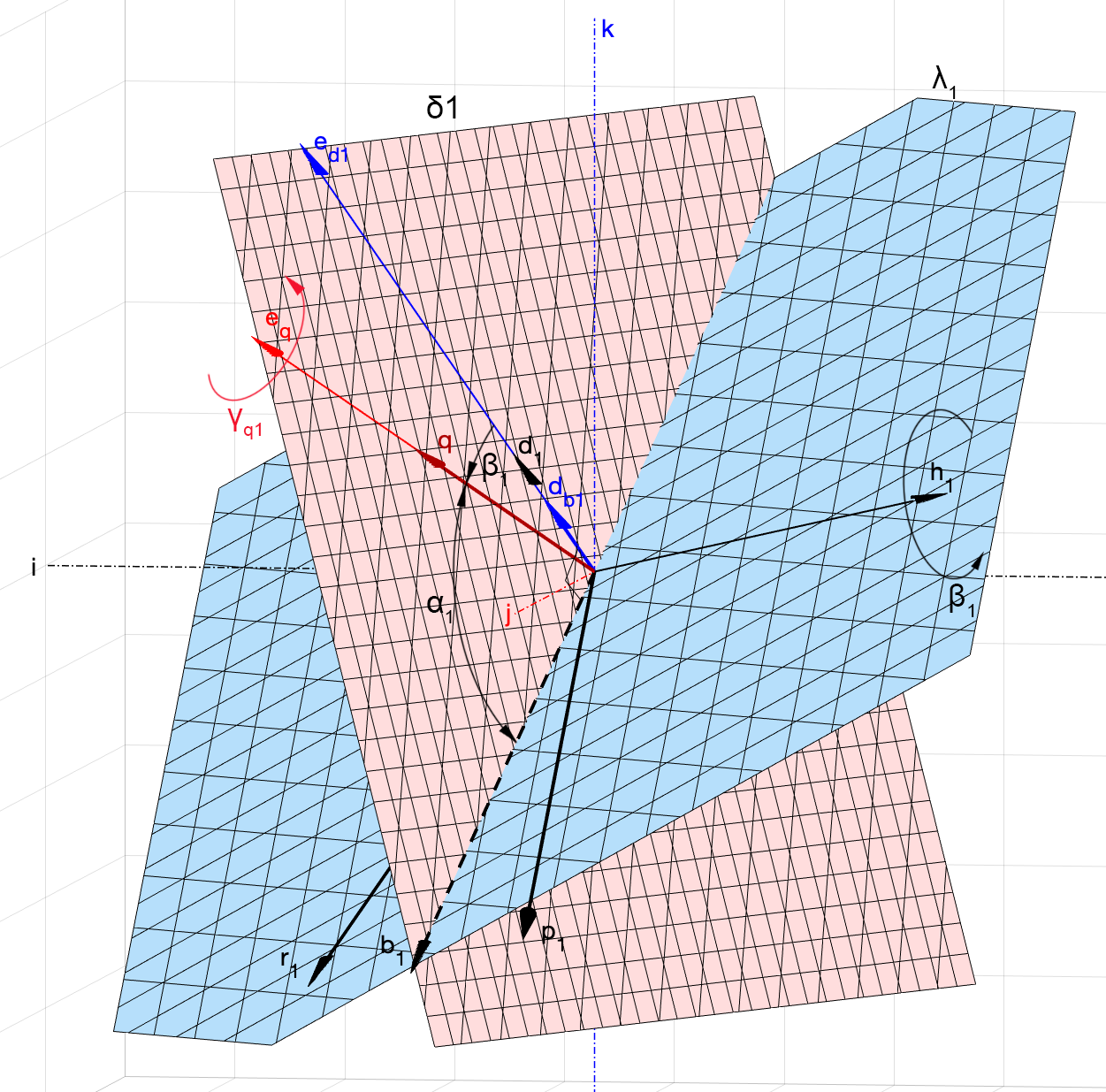
. 8. ,
, ..
,
,
,
.
,
.
2 ,
, , ,
. ,
,
, .
.
.
,
.
: . ,
,
.
, ,
. ,
, ,
, . ,
,
,
:
, . , ,
,
,
,
,
. "1" "2" " i ", , i = 1, 2 .
,
, :
:
,
:
;
,
,
:
;
1,
:
;
,
:
,
:
;
,
:
,
, ,
:
,
.
,
.
,
(. 3).
.
,
, :
- ,
,
:
.
.
- ,
. (17),
(19) (18), , (14), :
" " ,
, .
.
. 6, (. 9).
.
,
,
,
,
(..
). ,
.
:
.
),
(21) ,
,
, 1. ,
,
.
. .
,
, ,
. (9), (18), ,
, (22),
.
. (9),
. :
. (23) (9), :
,
,
. , :
.
. ,
,
( (11)),
. ,
,
,
. (23)
, :
,
(12) , :
, :
,
(24), (13) :
(29).
. (30), . , , . . 10 , .
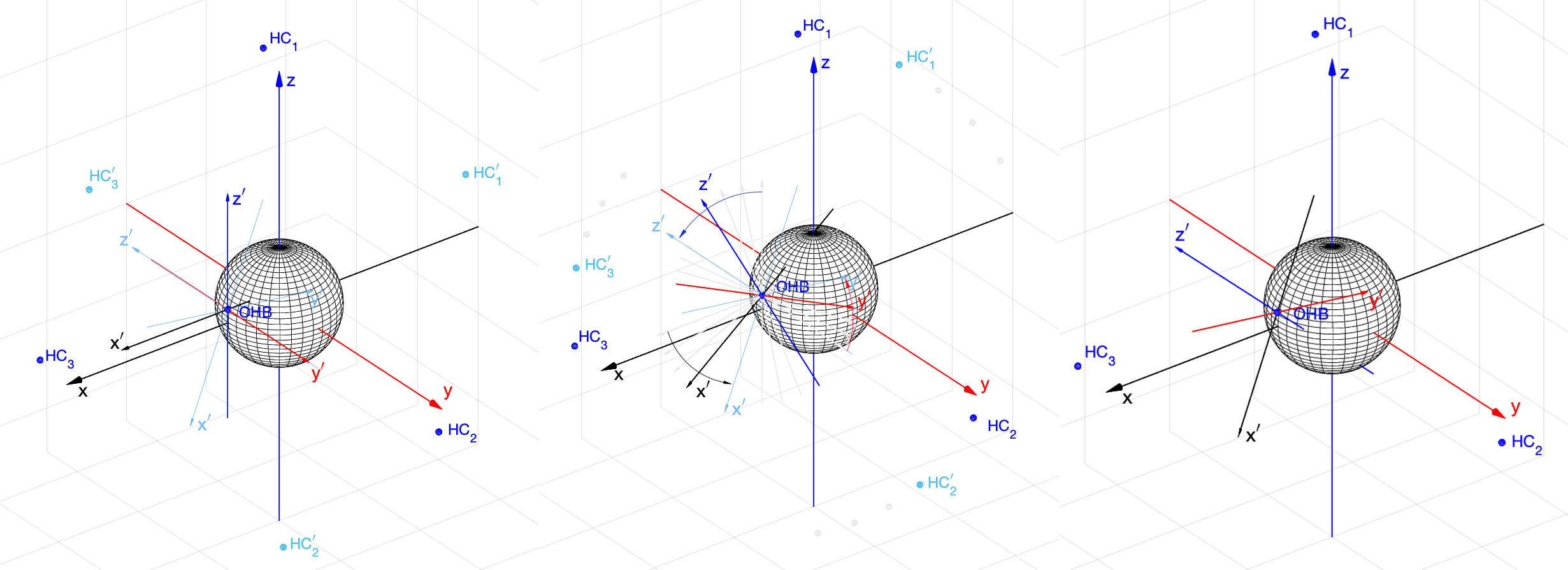
, , , , ( , "", , ). 1', 2' 3' 1, 2 3 (. 10, )). ,
(30) . . 10, ) 10 . ( - ) . . 10, ) ,
, (, , ).
That's all for now. I will only note that in the near future I will try to work on one drawback of expression (30). When close to zero, that is, when the orientations of the HSC and LSC differ little, the quaternion is
calculated with an error due to the multiplier
. This can lead to significant errors in calculating the orientation of the LCS and, as a result, errors in position determination
. More about this in the next article.