First impression
Forth is still known, mainly among the development of embedded systems, as something like an extraordinary high-level assembler, for example, for microcontrollers - AmForth and Mecrisp . However, once upon a time it was known in a different guise - as a programming language for scientific applications.

Fort was chosen as a means by which the details of the software implementation of knowledge-based systems are explained for the following reasons: firstly, a translator from this language is available on almost all types of microcomputers, secondly, it is quite cheap, and, finally , has a lot in common with artificial intelligence languages, in particular Lisp.
Townsend K., Focht D. DESIGN AND SOFTWARE IMPLEMENTATION OF EXPERT SYSTEMS ON PERSONAL COMPUTERS. Moscow: Finance and Statistics, 1990.
I read this and was impressed. Here are three books I know very well:

Programming languages in books, respectively - BASIC , Fortran and Fort! In T. Toffoli's book:
CAM-6 , , , .
CAM-6 , IBM-PC (XT, AT ), , PC-DOS2. , , , , , , ( ) CRAY-1. CAM-6 FORTH IBM-PC 256 . .
CAM Forth. Forth , . , , CAM ( , , ).
! , ! , , 80- 90-. , , - , , , - , , ... , : C. Clay Marston and Gabriel G. BalintKurti. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions // J. Chem. Phys. 91, 3571 (1989); doi: 10.1063/1.456888
1989 , - , , Matlab . - , .
, - HP 35s. - ( ). - .

, ( , ) , - .
see normcdf
: NORMCDF flit 1.41421 F/ ERF F1.0 F+ flit .500000 F* ;
ok
see erf
: ERF FDUP FSIGN FSWAP FDUP F* FDUP flit .147000 F*
FDUP flit 1.27324 F+ FSWAP F1.0 F+ F/ F*
FNEGATE FEXP FNEGATE F1.0 F+ FSQRT F* ;
ok
see fsign
: FSIGN F0< DUP INVERT - S>F ;
ok
see dup
DUP IS CODE ( $4012D8 53 )
push ebx
. - , . , . , , , , , - http://rigidus.ru/
, , . ? , , - . , , :(word) cvn { moveto show } def
{ moveto show } /S exch def
def () . Postscript, . : word moveto show ;
- , . ? . STATE=-1 (true ), , () STATE=0.
, . , , . - , . , . , . , , . :
Keep it simple
Do not speculate
Do it yourself
motherf*cker
, , - API. , - .
, - (, ) . , Intel 8087 - , ! :
: LNGAMMA ( x -- ln((x) )
\ Takes x > 0.0 and returns natural logarithm of (x).
FDUP 3.0E F+ 2.23931796330267E FSWAP F/
FOVER 2.0E F+ -27.0638924937115E FSWAP F/ F+
FOVER 1.0E F+ 41.4174045302371E FSWAP F/ F+
2.5066284643656E F+ FLN FSWAP
FDUP 4.15E F+ FLN
FOVER 0.50E F+ F*
FOVER 4.15E F+ F-
FROT F+ FSWAP FLN F- ;
, - - FDUP, FROT, FOVER
... , 4 . , . , .
- . , , . , : lngamma { f: x }
gforth. : lngamma {: f: x :}
VFX Forth. , , . - ?
, , . , :
variable apples ok
: +apples apples +! ; ok
: apples ." You have " apples @ . ." apples." cr ; ok
apples You have 0 apples.
ok
5 +apples ok
apples You have 5 apples.
ok
apples apples
, . , +apples
, . +apples
, . . , X. :
variable &x
: x &x @ ;
: (x) &x ! ;
: cube (x)
x x x * * ;
variable &x
: x &x @ ;
: (x) &x ! ;
: square (x)
x x * ;
3 square . 9 ok
3 cube . 27 ok
cube
square
. &x, x, (x) , , , . FORTH: .
F-PC Forth 3.60
FLOAD FFLOAT.SEQ
FLOAD EVAL.SEQ
: COMPARE ( c-addr1 u1 c-addr2 u2 -- n )
ROT
2DUP U< IF DROP COMPARE DUP 0= IF DROP 1 THEN EXIT THEN
2DUP U> IF NIP COMPARE DUP 0= IF DROP -1 THEN EXIT THEN
DROP COMPARE ;
: REFILL ( -- f ) \ CORE version for user input device and string only
loading @ IF ( file ) false EXIT THEN
'tib @ sp0 @ = IF ( user input device ) query true EXIT THEN
( EVALUATE ) false ;
MACRO: ++ PAD +PLACE ;
: (VARIABLE)
" VARIABLE &" PAD PLACE 2DUP ++
" : (" ++ 2DUP ++ " ) &" ++ 2DUP ++ " ! ;" ++
" : " ++ 2DUP ++ " &" ++ ( NAME ) ++ " @ ;" ++
PAD COUNT EVAL ;
: (FVARIABLE)
" FVARIABLE &" PAD PLACE 2DUP ++
" : (" ++ 2DUP ++ " ) &" ++ 2DUP ++ " F! ;" ++
" : " ++ 2DUP ++ " &" ++ ( NAME ) ++ " F@ ;" ++
PAD COUNT EVAL ;
: REFILL-AT-EOL? ( S: -- FLAG )
SOURCE NIP >IN @ > DUP 0= IF DROP REFILL THEN ;
: VARIABLES(
BEGIN BL WORD COUNT 2DUP " )" COMPARE
WHILE REFILL-AT-EOL?
WHILE (VARIABLE)
REPEAT
THEN 2DROP ;
: FVARIABLES(
BEGIN BL WORD COUNT 2DUP " )" COMPARE
WHILE REFILL-AT-EOL?
WHILE (FVARIABLE)
REPEAT
THEN 2DROP ;
:
\
VARIABLES( MAXIT )
FVARIABLES( ACCURACY UNLIKELY-VALUE )
\
-1.11E30 (UNLIKELY-VALUE)
1.0E-9 (ACCURACY)
50 (MAXIT)
\
MAXIT . 50 ok
, , , , . , x @ y @ + z !
x y + (z)
, @
f@
.
F-PC Forth
IBM PC AT, MS DOS , F-PC Forth. fpc36.zip, , dosbox. , .

IDE, , . IDE Borland .
F-PC Forth 3.60
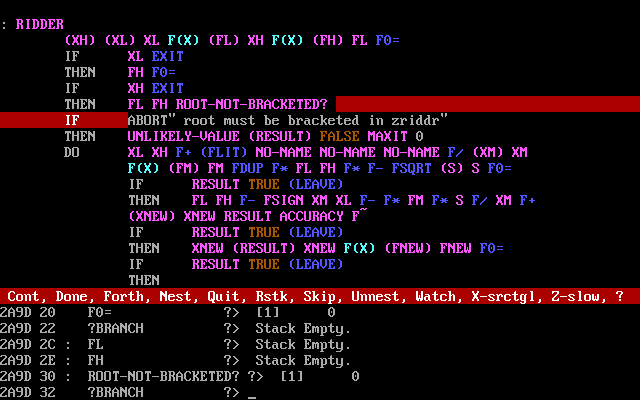

F-PC Forth 3.60
DEFER F(X)
VARIABLES( MAXIT )
FVARIABLES( XL XM XH XNEW FL FM FH FNEW S RESULT ACCURACY UNLIKELY-VALUE )
-1.11E30 (UNLIKELY-VALUE)
1.0E-9 (ACCURACY)
50 (MAXIT)
: FSIGN ( R1 -- R1 ) F0< DUP NOT - IFLOAT ;
: F~ ( R1 R2 R3 -- FLAG ) F-ROT F- FABS F> ;
: ROOT-NOT-BRACKETED? ( FL FH -- FLAG )
FDUP F0< FOVER F0> AND
( FB ) F0> ( FA ) F0< AND OR NOT ;
: RIDDER ( R1 R2 -- R1 ) (XH) (XL)
XL F(X) (FL) XH F(X) (FH)
FL F0= IF XL EXIT THEN
FH F0= IF XH EXIT THEN
FL FH ROOT-NOT-BRACKETED?
IF ABORT" ROOT MUST BE BRACKETED IN ZRIDDR" THEN
UNLIKELY-VALUE (RESULT) FALSE
MAXIT 0
DO
XL XH F+ 2.0E F/ (XM) XM F(X) (FM)
FM FDUP F* FL FH F* F- FSQRT (S)
S F0=
IF RESULT TRUE LEAVE THEN
FL FH F- FSIGN XM XL F- F* FM F* S F/ XM F+ (XNEW)
XNEW RESULT ACCURACY F~
IF RESULT TRUE LEAVE THEN
XNEW (RESULT) XNEW F(X) (FNEW)
FNEW F0=
IF RESULT TRUE LEAVE THEN
FNEW FSIGN FM F* FM F= NOT
IF XM (XL) FM (FL) RESULT (XH) FNEW (FH)
ELSE FNEW FSIGN FL F* FL F= NOT
IF RESULT (XH) FNEW (FH) THEN
FNEW FSIGN FH F* FH F= NOT
IF RESULT (XL) FNEW (FL) THEN
THEN
XL XH ACCURACY F~
IF RESULT TRUE LEAVE THEN
LOOP
IF RESULT DROP
ELSE ." ZRIDDR EXCEED MAXIMUM ITERATIONS" DROP THEN ;
: FUNC FDUP FEXP FSWAP -5.0E F* 3.0E F+ F+ ;
' FUNC IS F(X)
1.25E 1.6E RIDDER F.
, , : BASIC, Fortran 77, Pascal.
, ,
, . , , . .
\ Structures
: structure:
create ( structure name ) here 0 0 ,
does> @ ;
: +field
create ( field name ) over , +
does> @ + ;
: (cell) aligned 1 cells +field ;
: (float) faligned 1 floats +field ;
: end-structure ( addr size -- ) swap ! ;
, 1994. , F-PC , ANS Forth 94 , , win32forth, Gforth. , win32forth.
IDE , Windows ( wine ). , :
\ Arrays
structure: array-structure
(cell) .array-data
(cell) .array-type
(cell) .array-size
end-structure
: array: ( size -- )
create
0 here .array-data ! here .array-type ! here .array-size !
array-structure allot ;
: array-allocate ( vec -- )
>r r@ .array-size @ r@ .array-type @ * allocate throw r> .array-data ! ;
: array-free ( vec -- )
>r r@ .array-data @ free throw 0 r> .array-data ! ;
: array-element ( i vec -- *vec[i] )
>r r@ .array-type @ * r> .array-data @ + ;
, 3-5 . . .
code fs-array-element
pop eax
mov ebx, [ebx]
lea ebx, [ebx] [eax*8]
next c;
- The Forth Scientific Library Project, , . Do it yourself! , . . .
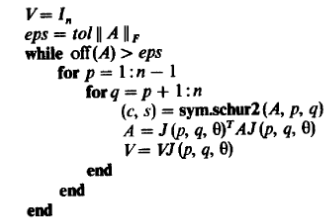
\ Cyclic Jacobi. Algorithm 8.5.3
\ Golub & Van Loan, Matrix Computations
fvariables( cos sin EPS )
variables( M EV MAXROT )
1.0e-10 (EPS)
50 (MAXROT)
: eig! (EV) (M)
EV matrix-set-identity!
MAXROT 0
do
M off-diagonal-norm EPS f<
if unloop exit then
M .matrix-rows @ 0
do M .matrix-cols @ i 1+
?do i j M sym.schur2 (sin) (cos)
cos sin i j M jacobi.rot'
cos sin i j M jacobi.rot
cos sin i j EV jacobi.rot
loop
loop
loop
." jacobi not converged" ;
, ? - , . eig
, , eig
.
, , C. Clay Marston and Gabriel G. BalintKurti. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions // J. Chem. Phys. 91, 3571 (1989); doi: 10.1063/1.456888 , , . , .

:
Fourier grid Hamiltonian (FGH) :
\ Equation 26
fvariables( l d/N )
: sum (d/N)
1.0e (l)
0.0e ( N ) 1 rshift 0
do [ 2.0e fpi f* ] fliteral
l d/N f* f* fcos l f**2 f* f+
l 1.0e f+ (l)
loop ;
variables( diags n )
fvariables( dx 1/n )
: FGH! (diags) (dx)
diags .array-size @ (n)
n s>f 1/f (1/n)
[ -8.0e fpi f**2 f* ] fliteral
1/n fdup fdup f* f* f* dx f**2 1/f f*
n 0 do i s>f 1/n f* n sum fover f* i diags fa!
loop fdrop ;
boilerplate code , , , . . , ? python/numpy, Matlab Julia - .

Fort could quite successfully replace Fortran and what else was there at that time. It's not so hard to live with postfix notation, stacks and deal with a level just above machine instructions. It is also important that the result of the process of working on a task in Fort will be either "not, well, to hell, where it has already been done, it is easier to write off", or a very deep understanding of every detail and essence of what is happening.
This is all philosophy, of course. However, I can imagine some kind of numerical Fort even now, in our time. It may be somewhere deep in the equipment of a cunning spectrometer, detector ... It would be interesting to know where.