Formulation of the problem
Many have heard of the ROC curve, which is often used in ML . Decoding this abbreviation, we get that ROC ( receiver operating characteristic ). Translated from English, this means RHP ( receiver performance ). This concept is borrowed from the theory of signal detection. The ROC curve can be associated with a radar station ( radar ), considering it from the point of view of object detection. Let's describe this more formally.
The radar sends out pulses that bounce off objects. The reflected signal is received by the receiving antenna of the radar ( Fig. 1 ). If there is any object located in the detection zone ( DZ )
, then the reflected signal will be higher than the detection threshold
and this will mean the presence of the object
. If the reflected signal is below the detection threshold, then this means that there is no object
.

ZO
The radar detection zone is the area of space within which the radar ensures the detection of objects with the probabilities of correct detection not worse than the required ones.
,
.
— . ,
, .
, , ,
. ,
, - , :
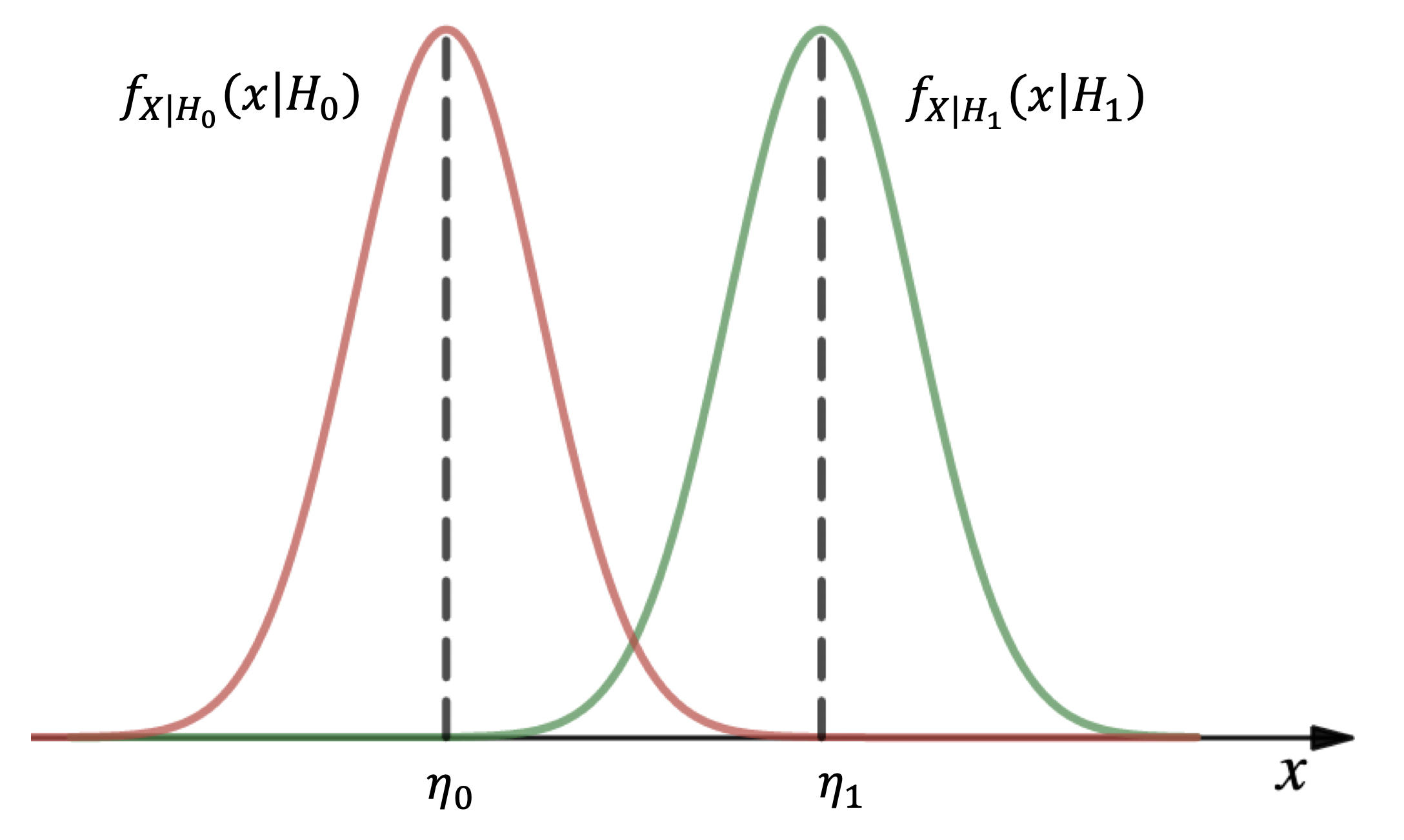
. 2 —
. ,
, ,
.
, ,
.
. . 2
, :
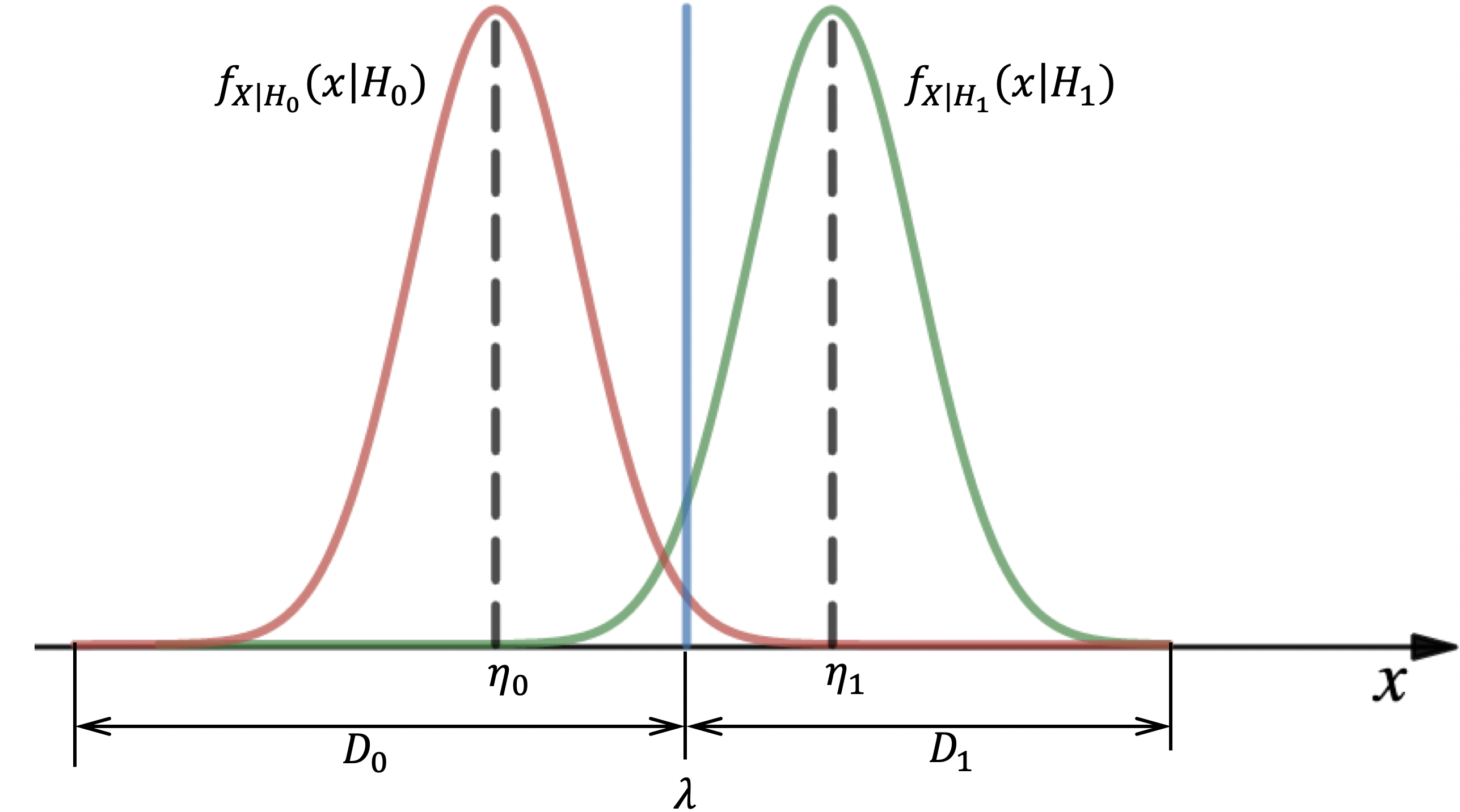
:
:
– ,
, .. .
– , ..
, ,
, .. .
, :
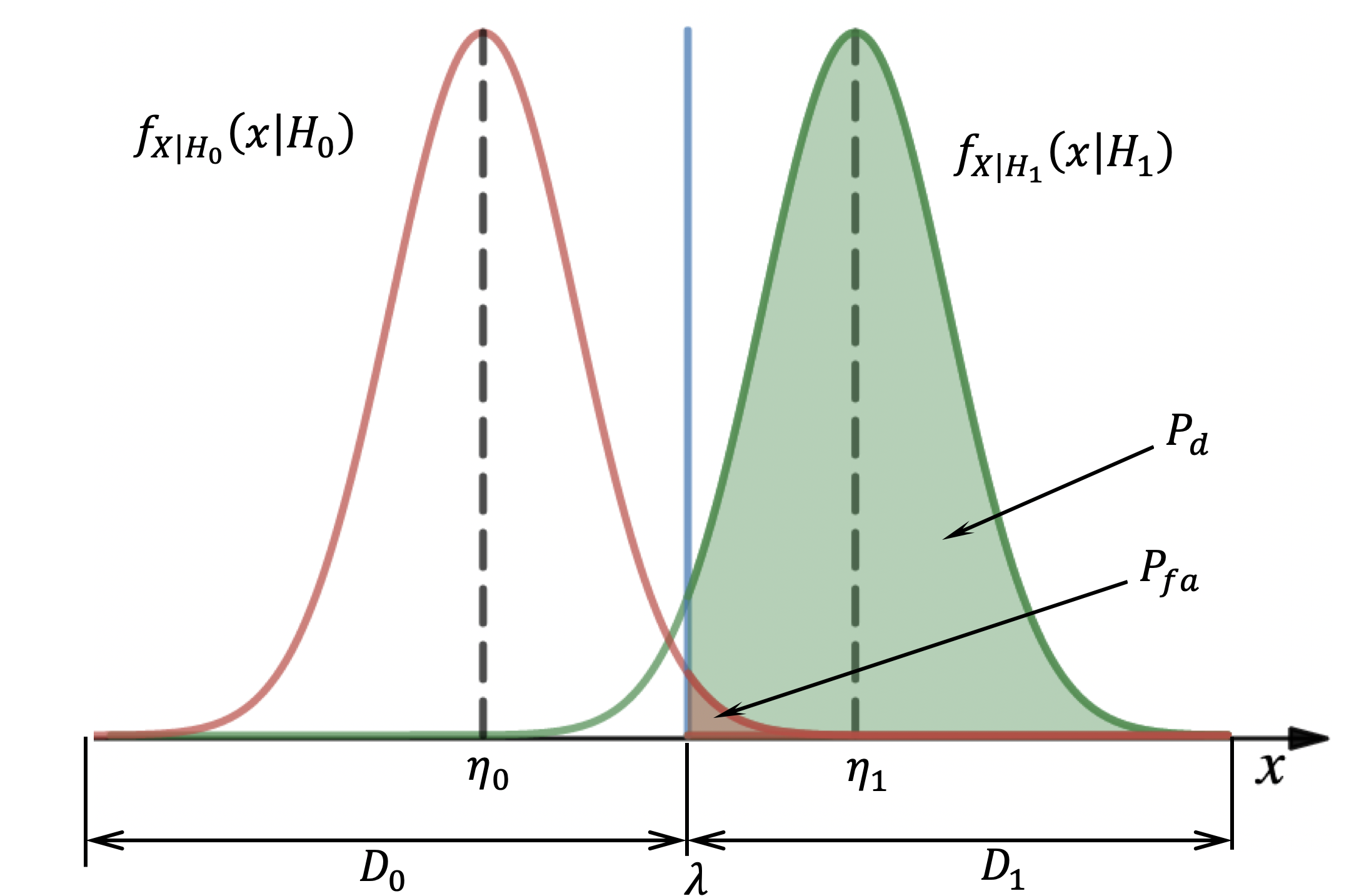
, , ,
.
,
, ROC- (. Receiver Operating Characteristic, ).
- (, . Signal-to-Noise Ratio, .
), :
– ;
– .
,
– , :
ROC-
:
, , , ..
,
–
.
.
, ,
,
.
,
.
:
, :
ROC- :
, ..
. ROC-
,
.
, :
– ROC- ROC-.
:
, ..
.
, ..
. , .
ROC-.
Python.
#
from scipy.stats import norm
from scipy.misc import derivative
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
%matplotlib inline
# SNR lambda
SNR_values = np.arange(-1, 5.5, 1/2)
lambda_values = np.arange(0, 1.01, 1/100)
# , sigma SNR
def snr_to_sigma(SNR):
return np.power(10, -SNR/20)
# , Pfa Pd sigma lambda
def roc_curve(sigma, lambda_):
return 1 - norm.cdf(lambda_/sigma), 1 - norm.cdf((lambda_ - 1)/sigma)
# DataFrame Pfa, Pd, SNR
data = []
for SNR in SNR_values:
for lambda_ in lambda_values:
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data.append([Pfa, Pd, str(SNR)])
data = pd.DataFrame(data, columns=['Pfa', 'Pd', 'SNR'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $SNR$', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 0.7, 0.05), fontsize=30)
plt.yticks(np.arange(0.5, 1, 0.05), fontsize=30)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR',
data=data, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.15, 0.81), xycoords='data',
xytext=(90, 150), textcoords='offset points',
size=30, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
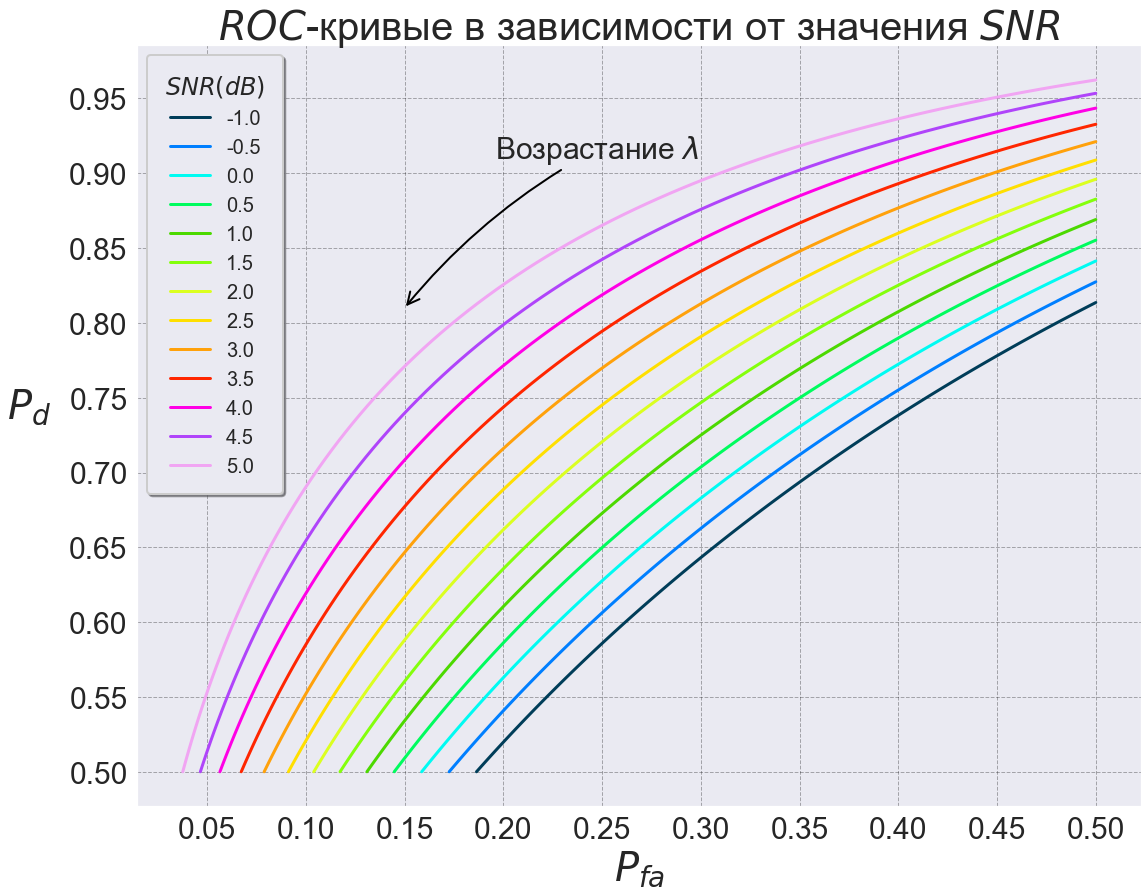
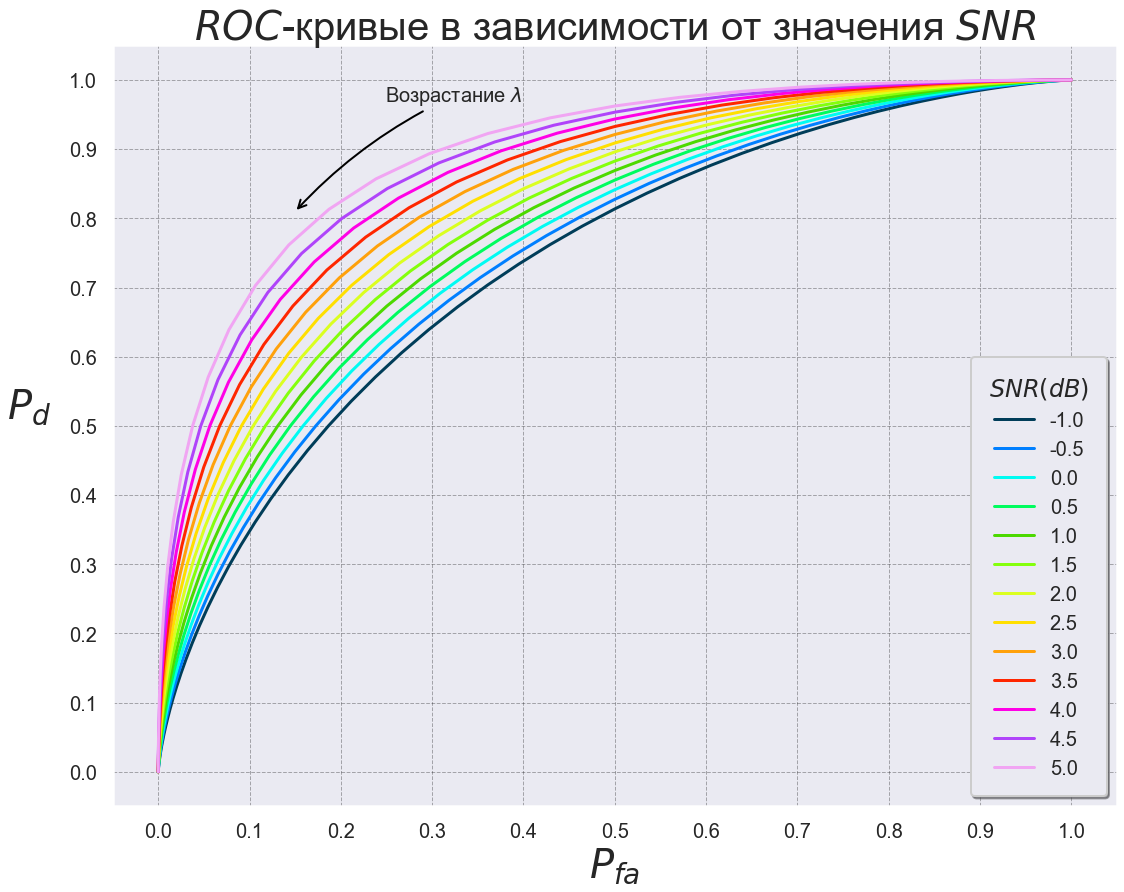
:
;
, ROC-
;
;
ROC - . , .
. , ROC-,
, ,
.
# DataFrame Pfa, Pd, SNR
data2 = []
for SNR in SNR_values:
for lambda_ in np.arange(-10, 10.1, 1/10) :
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data2.append([Pfa, Pd, str(SNR)])
data2 = pd.DataFrame(data2, columns=['Pfa', 'Pd', 'SNR'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $SNR$', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR',
data=data2, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.15, 0.81), xycoords='data',
xytext=(90, 110), textcoords='offset points',
size=20, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
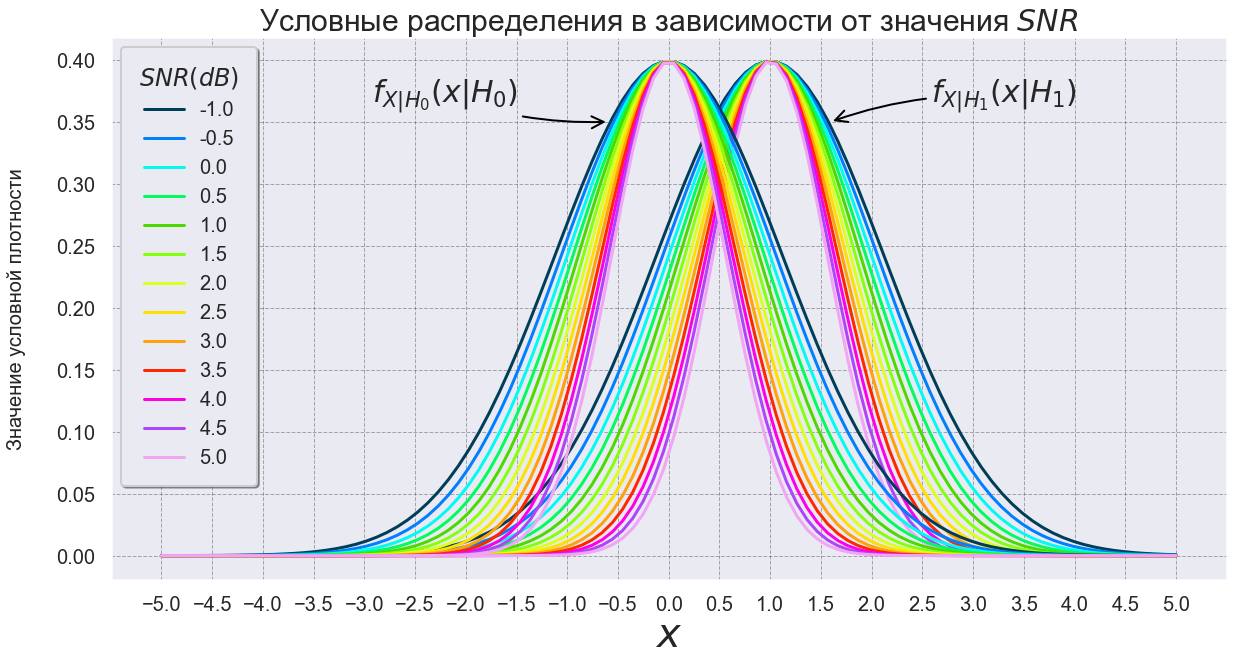
,
. ,
,
,
. ,
.
# , sigma
def conditional_density(x, sigma):
return norm.pdf(x/sigma), norm.pdf((x - 1)/sigma)
# DataFrame SNR
data3 = []
x_range = np.linspace(-5, 5, 100)
for SNR in SNR_values:
for x in x_range :
cond_dens1, cond_dens2 = conditional_density(x, snr_to_sigma(SNR))
data3.append([cond_dens1, cond_dens2, str(SNR), x])
data3 = pd.DataFrame(data3, columns=['cond_dens1', 'cond_dens2', 'SNR', 'x'])
fig, ax = plt.subplots(figsize=(20, 10))
sns.set_context('poster')
plt.title(' $SNR$',
fontsize=30)
plt.xlabel('$x$', fontsize=40)
plt.xticks(np.arange(-5, 5.5, 0.5), fontsize=20)
plt.yticks(np.arange(0, 0.45, 0.05), fontsize=20)
plt.ylabel(' ', fontsize=20,
labelpad=30)
sns.lineplot(x='x', y='cond_dens2', hue='SNR',
data=data3, palette='gist_ncar', ax=ax)
sns.lineplot(x='x', y='cond_dens1', hue='SNR',
data=data3, palette='gist_ncar', ax=ax, legend=False)
ax.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True, loc='upper left')
ax.annotate("$f_{X|H_0}(x|H_0)$", xy=(-0.6, 0.35), xycoords='data',
xytext=(-90, 20), textcoords='offset points',
size=30, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
ax.annotate("$f_{X|H_1}(x|H_1)$", xy=(1.6, 0.35), xycoords='data',
xytext=(100, 20), textcoords='offset points',
size=30, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3);
. 7 , , , , , .
:
data4 = []
for SNR in SNR_values:
for lambda_ in lambda_values:
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data4.append([Pfa, Pd, str(SNR), lambda_])
data4 = pd.DataFrame(data4, columns=['Pfa', 'Pd', 'SNR', 'lambda'])
fig, ax = plt.subplots(figsize=(16, 12))
sns.set_context('poster')
plt.title(' $P_d$ $\lambda$ $SNR$', fontsize=40)
plt.xlabel('$\lambda$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0.5, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='lambda', y='Pd', hue='SNR',
data=data4, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.5, 0.85), xycoords='data',
xytext=(-10, 50), textcoords='offset points',
size=20, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=-0.2"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
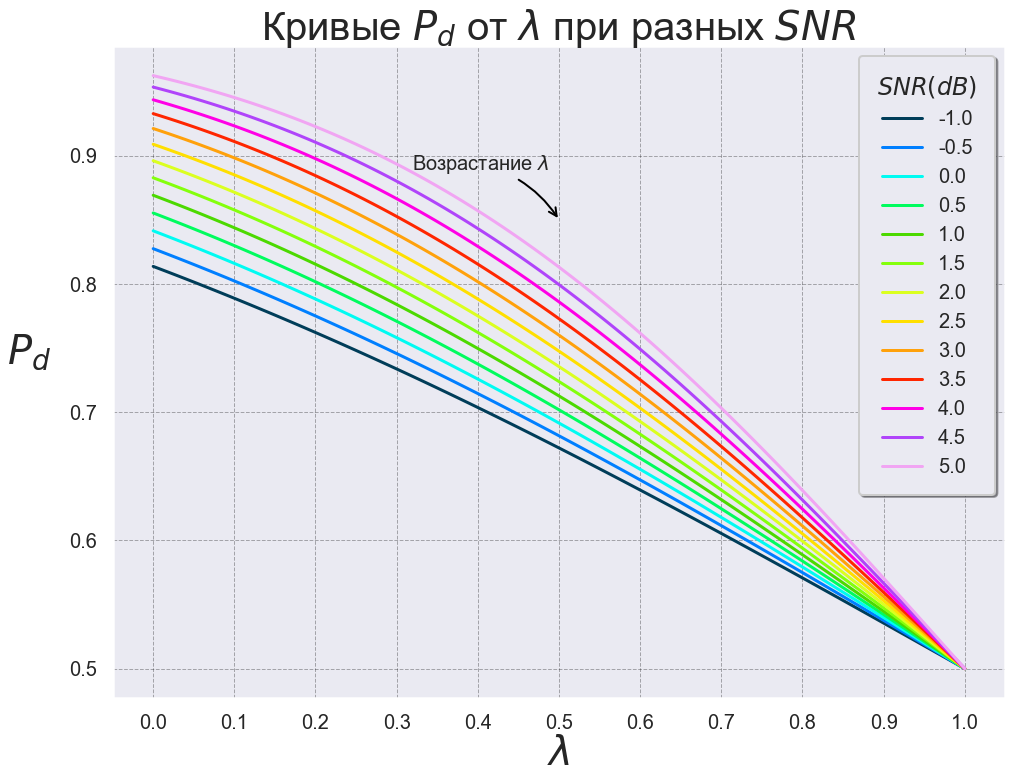
. :
fig, ax = plt.subplots(figsize=(16, 12))
sns.set_context('poster')
plt.title(' $P_{fa}$ $\lambda$ $SNR$', fontsize=40)
plt.xlabel('$\lambda$', fontsize=40)
plt.ylabel('$P_{fa}$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='lambda', y='Pfa', hue='SNR',
data=data4, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.5, 0.35), xycoords='data',
xytext=(-10, 90), textcoords='offset points',
size=30, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.2"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
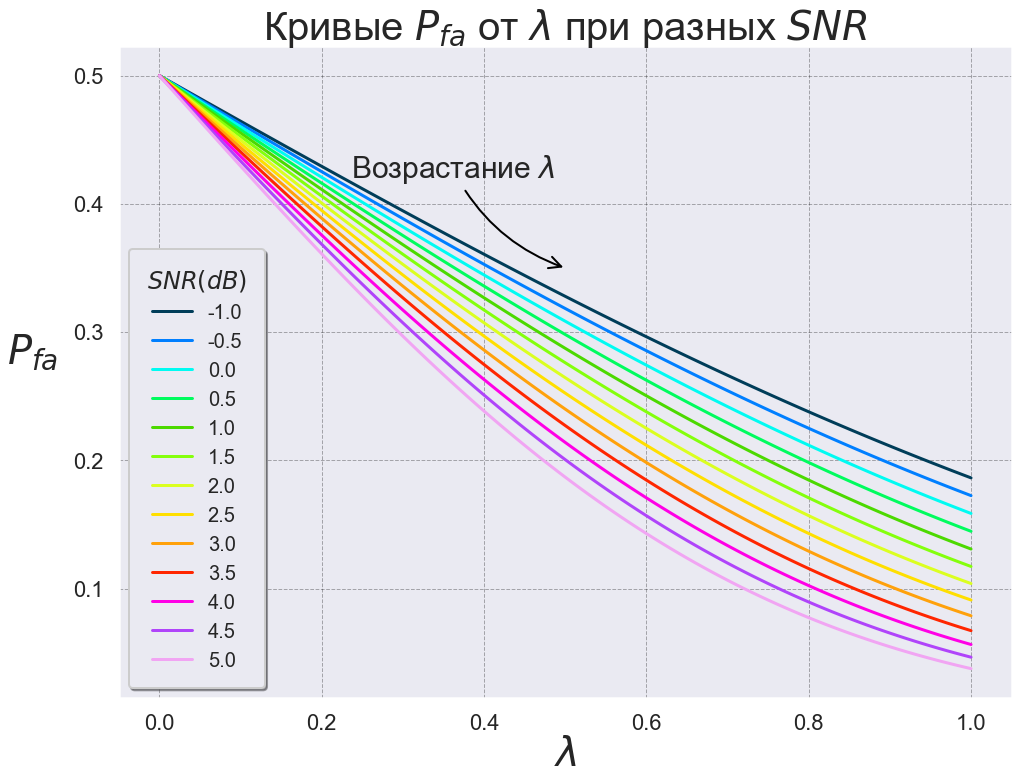
,
,
,
, .
, ROC-
,
.
:
:
, ROC-
. ,
, ,
.
,
, ..
( ).
# , Pfa Pd sigma lambda
def dif_roc_curve(sigma, lambda_):
return (derivative(lambda x: 1 - norm.cdf(x/sigma), lambda_, dx=1e-10),
derivative(lambda x: 1 - norm.cdf((x - 1)/sigma), lambda_, dx=1e-10))
data5 = []
for SNR in SNR_values:
for lambda_ in [0, 0.5, 1]:
dPfa, dPd = dif_roc_curve(snr_to_sigma(SNR), lambda_)
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
tan = dPd/dPfa
for i in np.arange(0.01/tan, 0.2/tan, 0.01/tan):
data5.append([tan*(i - Pfa) + Pd, i, str(SNR), lambda_])
data5 = pd.DataFrame(data5, columns=['y', 'x', 'SNR', 'lambda'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $3^{}$ ', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR', legend=False,
data=data[data['SNR'] == '5.0'], palette='gist_ncar', ax=ax)
sns.lineplot(x='x', y='y', hue='lambda', linestyle='--',
data=data5[data5['SNR'] == '5.0'],
palette='dark:b', legend=True, ax=ax)
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title=' $\lambda=$',
borderpad=0.9, fancybox=True, loc=4);
/
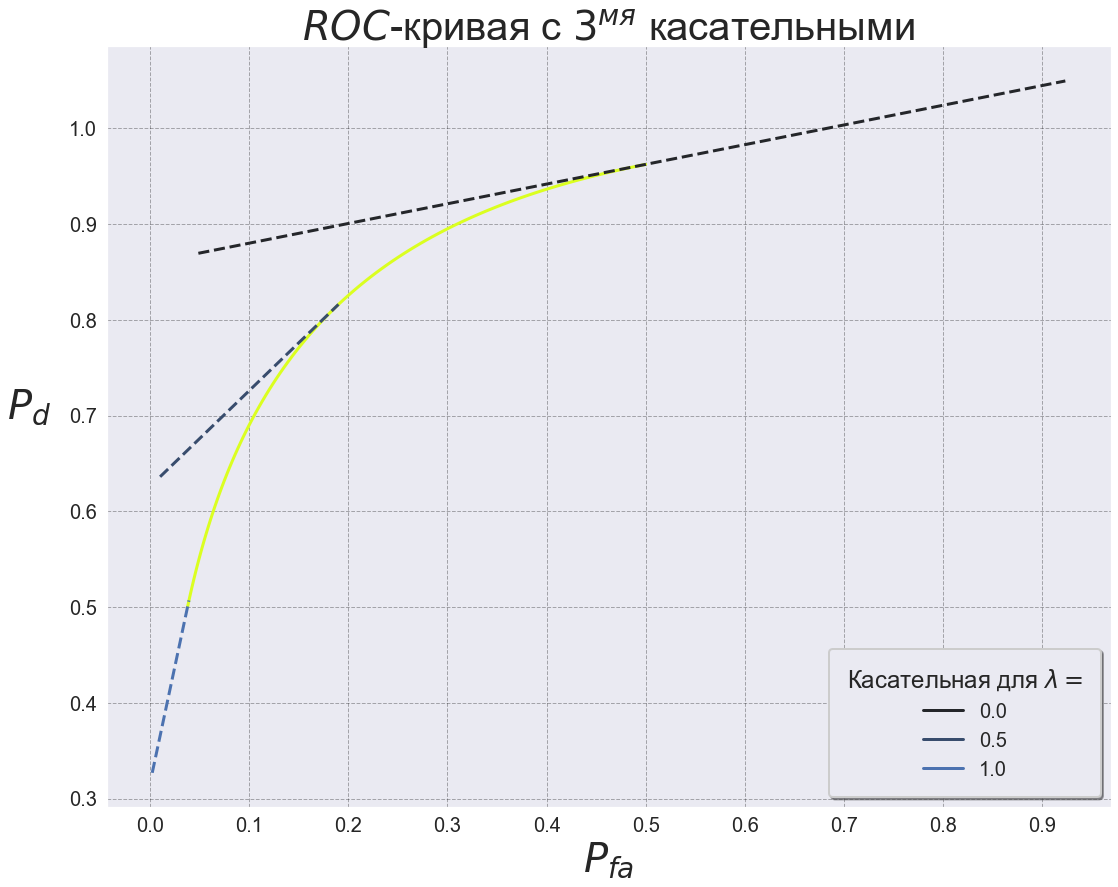
. 10 .
ROC- . ROC- . , ,
,
. , ROC-,
.
- . , . 1. , --, 1968, , . , . . . . . ., « », 1972, 744 .
Tyapkin V.N. Fundamentals of building radar stations of radio-technical troops: textbook / V.N. Tyapkin, A.N. Fomin, E.N. Garin [et al.]; under total. ed. V.N. Tyapkin. - Krasnoyarsk: Sib. Feder. un-t. - 2011 .-- 536 p.
Additionally
Link to github with source code.