Illustration: Daniel Grizely / Getty Images
It's fun to think about how we learn something. For example, the mass of the Sun is about 2 x 10 30 kg. This is such a huge number that it is difficult to comprehend it. And if it's so hard for us to even imagine such large numbers, how are we going to look for these values? Well, the original method was to use small masses, stick and rope. Perhaps this is one of the important steps in determining the mass of both the Sun and all the planets in our solar system. This is a Cavendish experiment pioneered by Henry Cavendishin 1798. The experiment is really cool, so I'm going to explain how it works.
There is gravitational attraction between objects with mass. The basketball has a gravitational interaction with the Earth (since they both have mass). It is this gravitational interaction that makes the basketball accelerate as it hits the ground if you release it. Naturally, everyone always knew that if you let go of an object, it would fall. However, it was only around Newton's time that people realized that this attraction also acts between astronomical objects such as the Earth, the Moon, and the Sun. This gives us a model for the interaction of forces, often referred to as Newton's law of gravity, but like most big ideas, it must have had many co-authors.
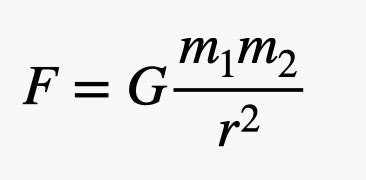
Art by: RHETT ALLAIN
Let's take a look at this gravitational force model. First, the magnitude of this force depends on the product of two interacting masses (m 1 and m 2 ). Second, the value decreases in proportion to the square of the distance between the two objects (r). Finally, there is G. This is the universal gravitational constant. This is the key to determining the mass of the earth.
So let's take a step back for a moment. When we measure things, we always have to make some choice. If we want to get the mass in kilograms, then we must decide how to indicate the value of 1 kg. We can say that a kilogram is the mass of 1 liter of water. Of course, this is not the best definition (we now have better methods). Okay, how about measuring strength? We use a unit called Newton, where 1 Newton is the force required to accelerate a body weighing 1 kilogram by 1 meter per second squared. Yes, the situation is getting out of hand, but the main thing is that you can give these definitions and plot one unit of measurement on top of another.
Now imagine this experiment. Suppose I take a liter of water (which I know is 1 kilogram) and measure the gravitational force coming from the Earth. If I know the radius of the Earth (the Greeks did a great jobwith its calculation) and the gravitational constant G, then I can solve the equation of gravitational force for the mass of the Earth (see above). But what is the gravitational constant? This is the tricky part, and this is how you can find the G value.
It turns out that this gravitational constant is very small. This means that the attraction between two common objects, such as water bottles, is ridiculously small. The only way to get a noticeable gravitational force is if one of the interacting masses is huge (like the Earth). However, there is a way to figure it out - to use a torsion balance.
Let's start with a simple physics demo that you can try at home. Take a pencil and place it on the edge of the table so that about half of the pencil hangs over the edge, as if it is about to fall, but holds. At this point, the pencil is basically balancing right on the edge of the table. The pencil only supports this tiny point of contact, so the frictional force cannot induce a torque to stop it from rotating. Even a very small amount of pressure on the end of the pencil will cause it to rotate. You just need to blow for the pencil to start rotating.

Video: RHETT ALLAIN
I like to put my fingers up to the pencil and pretend I'm using my superhero powers to move it. Now let's replace the pencil with a longer stick, and instead of placing it on the table, I would hang it on a string. Since it rests in the middle, a tiny amount of force is enough to make it rotate, just like with a pencil. Instead of blowing, we could make a small gravitational force move it. This is how it works.
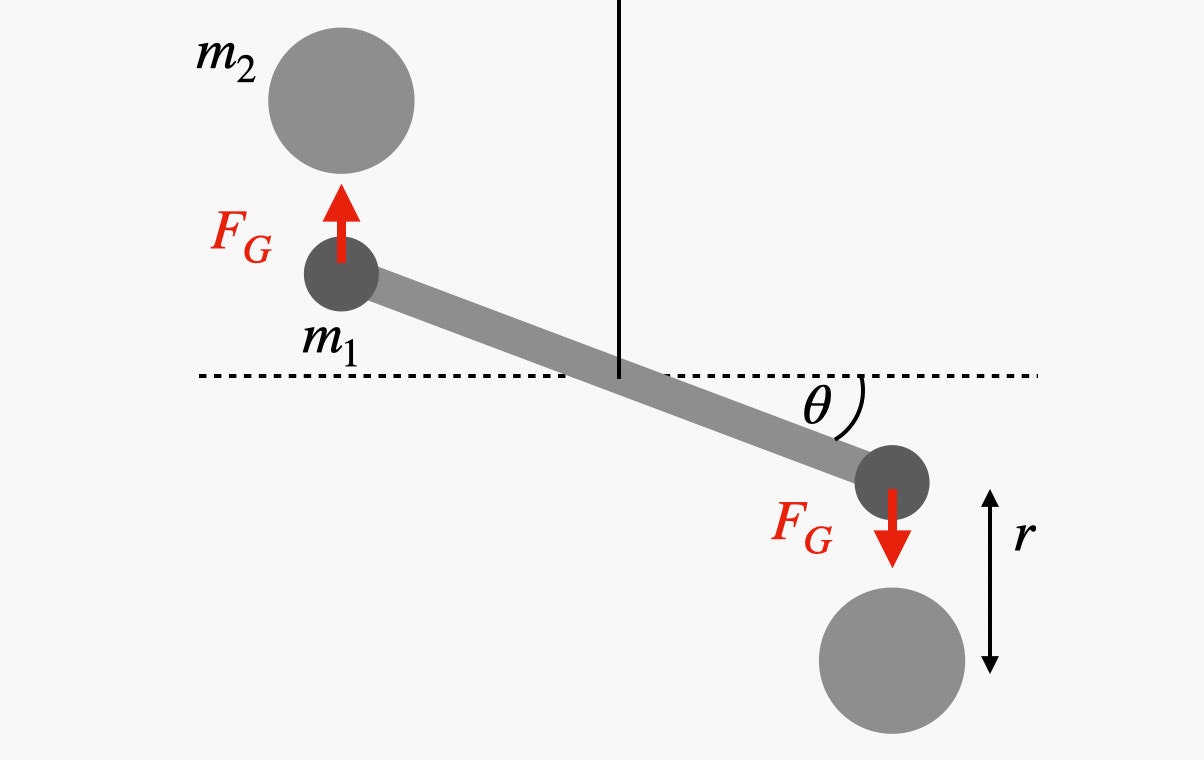
Illustration: RHETT ALLAIN
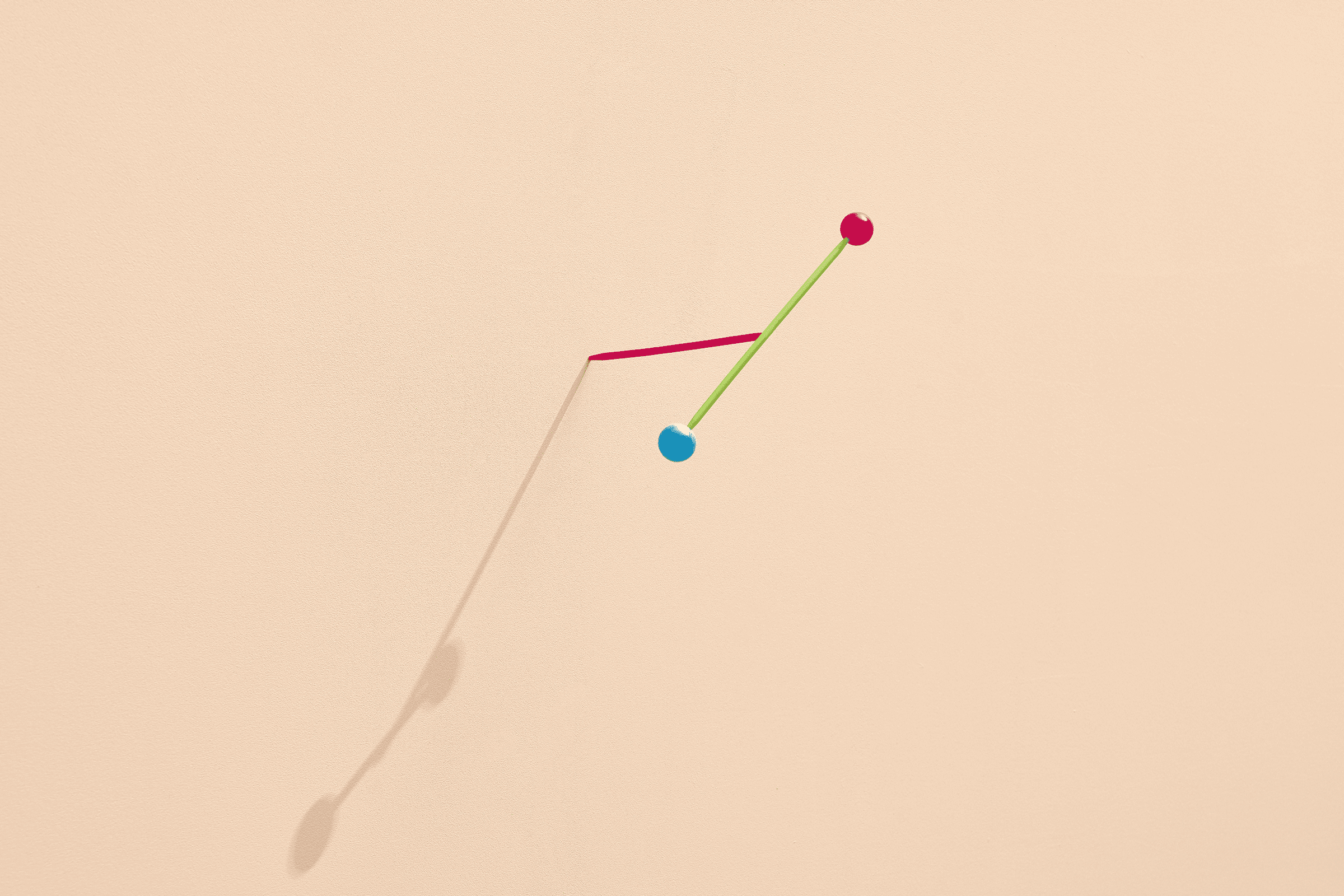
There are two smaller masses at the end of the rotating horizontal bar (labeled m 1 ). These masses interact with large masses (m 2) that are at a distance (r) from them. The horizontal bar will eventually reach some equilibrium position because a small amount of torque is generated by the twisting of the cable that supports the bar. The cable acts like a rotating spring. The more it twists, the greater the torque. If you know the relationship between the angle of rotation (θ) and the torque, you can calculate the gravitational force that pulls the mass at the end of the stick towards the larger stationary mass. In the configuration in the diagram above, large masses will cause the stick to rotate clockwise (as seen from above). If you move more masses to the other side of the stick, gravitational forces will cause it to rotate counterclockwise. This shows that the rotation is due to the gravitational interaction between the paired masses.Once the stick takes a stable position, all that remains is to measure the masses and the distance between them in order to obtain the gravitational constant.
In this case, we get the gravitational constant G = 6.67 x 10 -11 N * m 2 kg 2 . You can see that this constant is really very small. As an example, we can demonstrate how the calculation is done. Suppose you are a person standing at a distance of 1 meter from another person of the same mass (about 75 kg). What amount of force will act on you due to gravitational attraction? Substituting these values (together with the constant) into the force equation, we get:
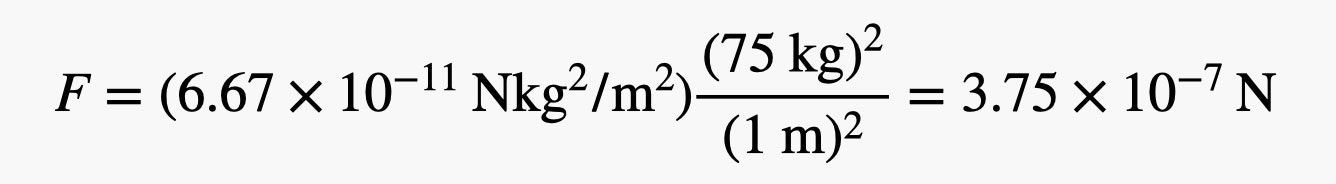
Illustration: RHETT ALLAIN
But that doesn't make sense. No one can feel so little power. Let's try to imagine a situation with a force comparable to the gravitational attraction between two people. How do you like that? Suppose you place a small object in your hand. You can feel the gravitational force of the Earth on this object because your hand has to push it upward to balance the gravitational force. What mass object will create a gravitational force caused by the Earth, equal to the force of attraction between two people? On the surface of the Earth, some of these values are always the same (gravitational constant, Earth's mass, and distance to the center of the Earth). We can group all these values into one number.
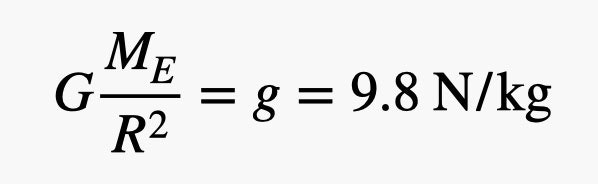
Art by: RHETT ALLAIN
We can call this the local-Earth gravitational constant. All you have to do is take the mass and multiply by "g" (we use the lowercase "g" to avoid confusion with another gravitational constant "G") and you get the gravitational force (weight). In this case, you would need an object about 4 x 10-11 grams to get a weight equal to the gravity between two people. This is still too little to understand. And if so? Human hair can have a linear mass density of 6.5 grams per kilometer (information from this publication ). This means only 6 x 10 -6 hairs millimeters has a weight equal to the attraction between two people. This is incomprehensible to the mind. Here's a bonus, my calculations , if you want to change the values.
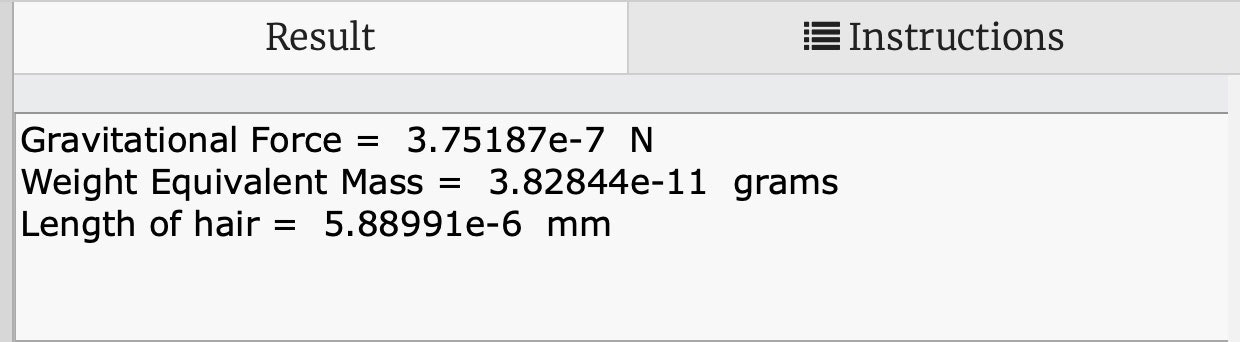
Illustration: RHETT ALLAIN
Oh yes, you can repeat the same calculation, but use a known mass and calculate the mass of the Earth. This is about 5.97 x 10 24 kilograms. But why stop there? You can also use the G value to find the mass of the sun. I will briefly explain how this calculation works.
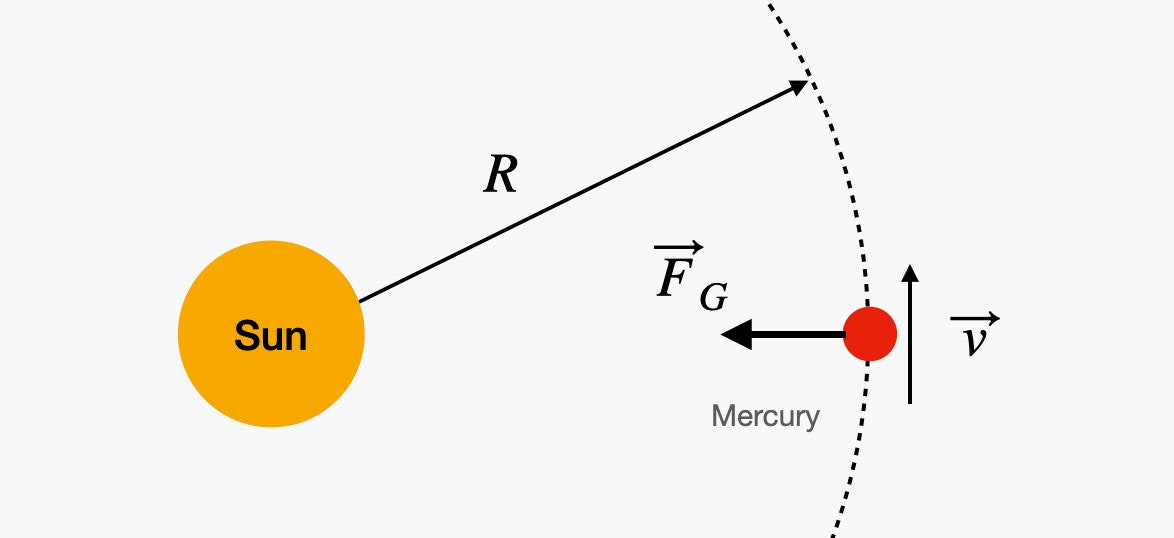
So, you have a planet like Mercury that revolves around the Sun. If we take into account that the orbit is circular, then the gravitational force from the Sun acts on Mercury.
Art by: RHETT ALLAIN
Gravitational force causes the planet to accelerate and move in a circle (centripetal acceleration). But this centripetal acceleration depends on both the angular velocity (ω) and the orbital distance (R). Since there is only one force acting on the planet (gravitational force), it will be equal to mass times acceleration, and the result will be the following ratio.
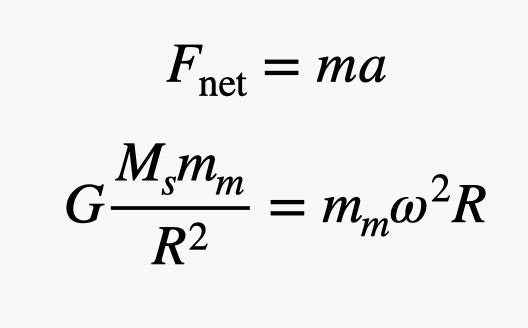
Illustration: RHETT ALLAIN
Note that the sun is assumed to be stationary here, which is generally correct. The mass of the Sun is colossal compared to the mass of Mercury, so the mass of Mercury does not matter. So, the solution for finding the mass of the sun:
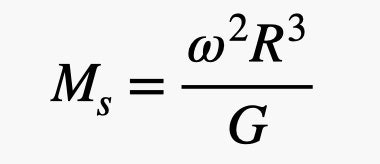
Illustration: RHETT ALLAIN
Now you just need to find the distance from the point of the orbit to the center of Mercury. You can do this by starting with the radius of the Earth . Then you need to find the angular velocity - you can get it by looking at how long it takes for Mercury to complete a revolution around the Sun. After that, everything is ready. You have a gravitational constant and you can calculate the mass of the sun. It's amazing that it all starts with some small masses on a horizontally rotating stick, but it's true.