On December 19, 2020, an article "Intuitive explanation of the integral" was published on Habré .
In the comments to it, some users indicated that the explanation was not very intuitive, for example:
“The topic itself is interesting, I recently repeated the course again, but I must say that, in my opinion, there is no zest in the material. The author is right that in modern publications, topics are often given without a description of their applied application, which is why the meaning of their study is not clear.
But specifically, integrals are a topic that needs to be described either shorter than yours, or much longer.
Otherwise, the student will not understand, and those who know will not discover anything new. "
I will try to present the material as short and simple as possible. So that the students finally understand, albeit with the help of their parents. So:
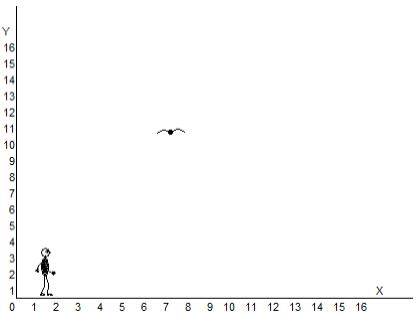
I live on a plane and my world looks like this:

All my movements are limited to a straight line, which I call the "abscissa axis" and denote it by the Latin letter x . Thus, I can walk from the point indicated by the number zero (my house is located there), to the right to infinity and back, to zero. The numbers on the abscissa let me know how far from home I am. I am now 10 divisions away from him.
, , , , : -1, -2 . ., . , , .
- , , , «». , , , . . (), :
: , ?
: , .
: ?
: — .
: «»? , , .
: «» , ( ) . , . — . , . , «» - .
, , , :

() . ...
: , «»?
: , , ? , 6 . . , , 8. . , . , «» ( ) .
(6, 8). — , — . .
, (.., 13,5 13.5) , .
: , ?
: :
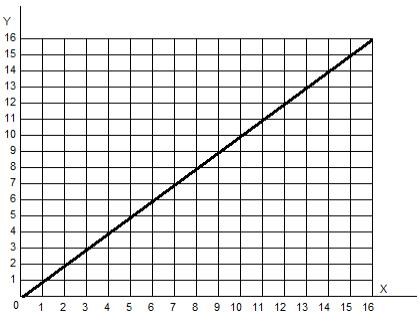
, , .

(4, 4) (10, 10), 6 . , 6 (). . , 6 .
- (, ), d (). dy, — dx. , , d = 6, dx = 6.
(dy/dx), : 6 / 6 = 1.
. = 1*.
, , . , , , 15, 15. — , , .
, , , , , -, - (0, 0). -, , . . :

, , , . , . ( ), , , 10. , , , 10 . , ( ) 5 . 10 5, 2. — — . ?
: , . , , , (5/10), 0.5, 1/2. ?
: ! () . , . ( ) , . — . 2, , , 0.5. , , = 2 = 0.5.
. , - , ( ), - , , . . , = 12 , = 0.5, , 12 , , 6.
, , : f(x) = x. , . , , f(x) = 2x f(x) = 0.5x. , ?
: . ?
: . , , () = x2, f(x) = x2. , .
, () . = x2 1, 2, 3 .. . 1:
y = 2 = 12 = 1.
, , 1, 1. :

, 2:
y = x2 = 22 = 4.
, (2, 4). 3 4, (3, 9) (4, 16) . :

, :

y = x2. , , = 1,5, , 1,5 . , (1.5, 2.25). , , ( ).
: - , . , , . , , . :

, ( (0, 0)), (3, 9). 9 , , 3 . , : 9 / 3 = 3. , , , 3. , 3, , , , , ! . . ? , , ? .
, - . , , — . , . , .
f(x) = x2 : , , . , 1: f '(x) = 2x.
f: f '(x) — , . .
? - f(x) = x2? . , , . , , , 1 . , :
f '(x) = 2x = 2*1 = 2.
1 .
4 ( = 4)? f '(x) = 2x = 2*4 8.
, 4 8. , , . ( ).
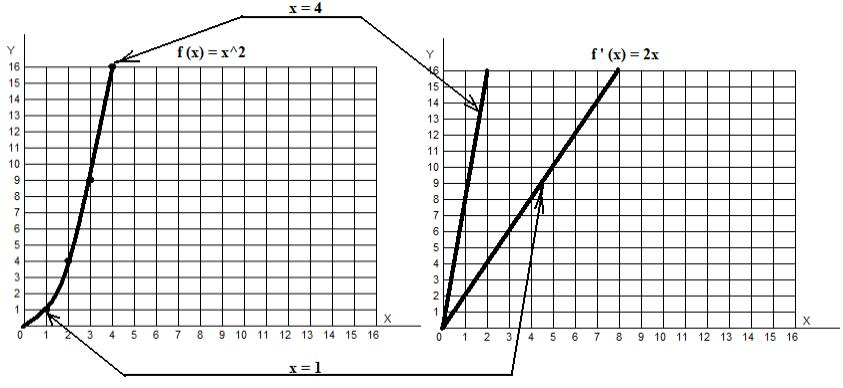
— , — , . , , . « , ».
f (x) = x.

: , ( , 1). , . , (, ( ) 1).
f(x) = x. : f '(x) = 1. ? , 1. , dx, dy . , , .
, ( ) . ?
, f(x) = 5. , ( ) 5, , dy ( ) .

, , , . , (dy/dx = 0/dx = 0).
: (, ), . , , .
: , : , — . , ?
: . . () , .
: , ? , f(x) = 5, :

, 5, , : 10 - 3 = 7. , 7, , 5 * 7 = 35 . 35 .
, ( ) .
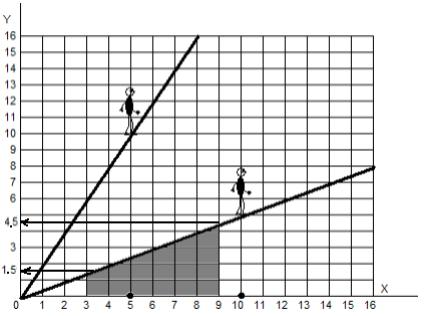
, , : 9 - 3 = 6.
: . ( ) , :
(1.5 + 4.5) : 2 = 3. — . 18. , 18 , ? , y = x2?

, 4 - 1 = 3 , ? 1 16, ? ?
: . «». , f (x) = x2 : f '(x) = 2x.
, , . , , . , , , , — .
(),
f(x) = x2 => f '(x) = 2x,
: , , : f '(x) = 2x => f(x) = x2 . . , , .
, ,
f (x) = x2 + 4:
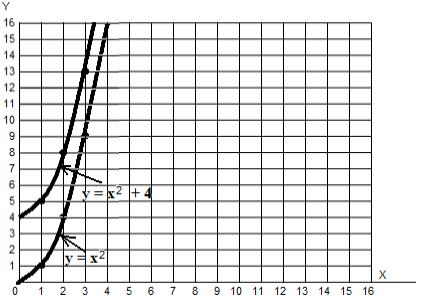
, f (x) = x2 , . , , , f (x) = x2 ! , f '(x) = 2x. () .
: ?
: , . , () ? , , 3 . ! , . , , . .
— , . , f (x) = x2 f (x) = x2 + 4 f '(x) = 2x.
: , , , , f (x) = x2 + 5 f (x) = x2 + 1.3 f (x) = x2 - 2 ? , , , ?
: , . f (x) = 2x F (x) = x2 + C, . , . , , , = 0. , , 4 .
, F — (), «» , , .
, F (x) = x2 + C, . :

f (x) = x2. , . 2, , x3. ( ). F (x) = x3/3 + .
.

, — 4 ( ):
F (x) = x3/3 = 43/3 = 21 1/3 ( )
:
F (x) = x3/3 = 13/3 = 1/3 ( )
: 21 1/3 - 1/3 = 21
21 . .
. , () f(x), .
() - , f '(x), , . , ( ) , .
, F, , , , . .
: ? , f (x) = x2 f (x) = x2 + 4, , ?
S: Do not worry, when you find the integral of the second function, the constant 4 in its antiderivative will turn into 4x , therefore, a rectangle with a height of 4 cells will be added to the area under it and there will be no error. So which road do you choose?