
Today NASA tweeted a message about the beginning of the movement of the Perseverance rover across the Red Planet. The rover drove a few meters to check the chassis. Everything ended well, the systems are working as they should. In addition, the rover has photographed its own tracks. The total arrival time is 33 minutes, during which time the rover covered 6.5 meters.
As far as you can tell, the rover is doing well. But, if you remember, the rover landed on the surface using the Sky Crane. The system, which provided a soft landing with the help of the cables, at some point separated from the rover and flew away, using the remaining reserves of fuel. But where exactly did she go and how far could she go? Let's count yourself.
NASA has already uploaded a photo of the platform that fell to the surface of Mars. The agency knows its exact location. But it's cool to calculate how far the platform has moved, having at its disposal the initial landing data and the video sent by the rover.
For calculations, we will use the angular size of the landing platform.
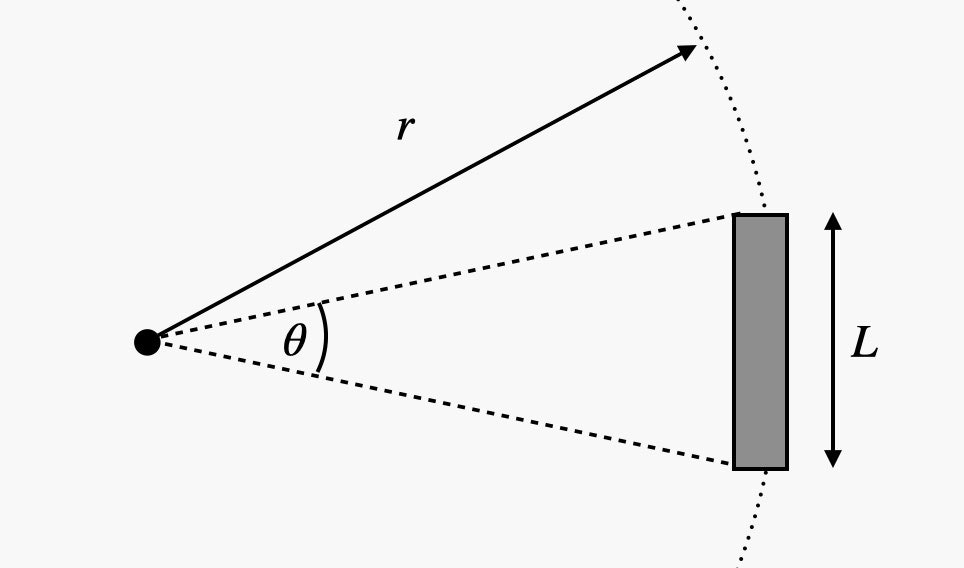
On Habré it hardly makes sense to talk about what the angular size is, so let's get down to the calculations right away.
Calculating the angular size is very simple, here is the formula.
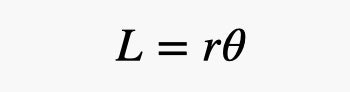
Why do we need angular size? Well, if we know it, plus we know the real size, then we can easily determine the distance to the object - it will be r. The ideal computation option is to use just a flat peg, it is easiest to carry out calculations with it. But since we have not a peg, but a platform, it will be a little more difficult. But still, there should be no problems during the calculations.
The first thing I should do is determine the field of view of the rover's camera pointing upwards. There are no exact characteristics, so let's estimate approximately. Here is a platform with the rover suspended from a cable before landing.

According to NASA, the cable is 6.4 meters long - so we know the ® in this photo. In addition, we can determine the length of the landing stage. If we take its width, it is 2.69 meters, then the real angular size, as seen from the rover, is 0.42 radians. Let's use this number to set the width of the entire video frame with an angular field of view (FOV) of 0.627 radians (that's 35.9 degrees).
All this is extremely important for further calculations. With this data, you can measure the angular size of the landing platform and calculate the distance to the rover. In order to do this, you can use a special tool, Tracker Video Analysis. It makes it possible to analyze the size of objects in the video. We build such a schedule.
One would think that the graph would be parabolic, which would show constant acceleration of the platform. But it seems that nothing of the kind happened - if the platform accelerated, then it was minimal. We calculate the speed - and we get about 8.2 m / s.
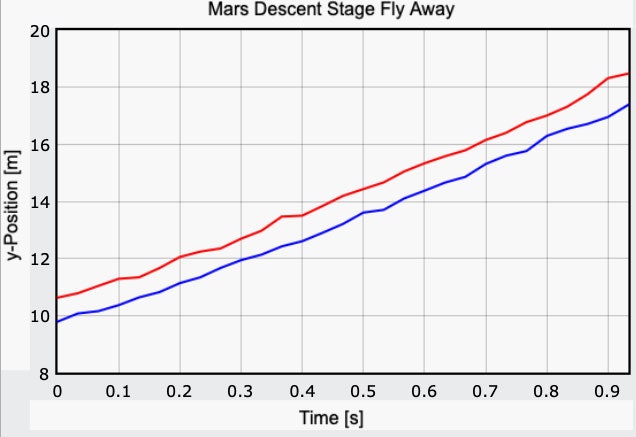
Stop! After all, we have something else. The fact is that the landing platform leaves at an angle, as has been said more than once. And this makes sense - if the platform just flew up, then after using all the fuel, this whole structure would then collapse downward - right onto the rover. The video makes it possible to determine the angle of inclination. Here is a graph and a formula that helps.
Using the known distance to the motors, as well as the apparent distance, we get an angle of inclination of 52 degrees from vertical. Let's hope that everything is correct, since this indicator is needed for further calculations.
Platform movement
We are now ready to tackle an important physical problem. It sounds like this.
The lander on Mars is performing a departure maneuver to get to a safe distance from the Perseverance rover. The module starts the thrusters to achieve a speed of 8.2 m / s at a launch angle of 52 degrees from vertical. If Mars has a gravitational field of 3.7 N / kg, how far from the rover will it fall? You can assume that the air resistance is negligible.
There is a formulation of the problem. Now we need an answer. The key point here is that the movement in the horizontal direction (let's call it the x-direction) is done at a constant speed. As for the speed of descent (y-direction), here we have an acceleration - g (where g = 3.7 N / kg), caused by the force of gravity. Since it is constant and acts only vertically, we can divide the task into two - in fact, movement in the horizontal plane and movement in the vertical one. These two elements of one task are independent, they are connected only by time.
Let's start by moving vertically.

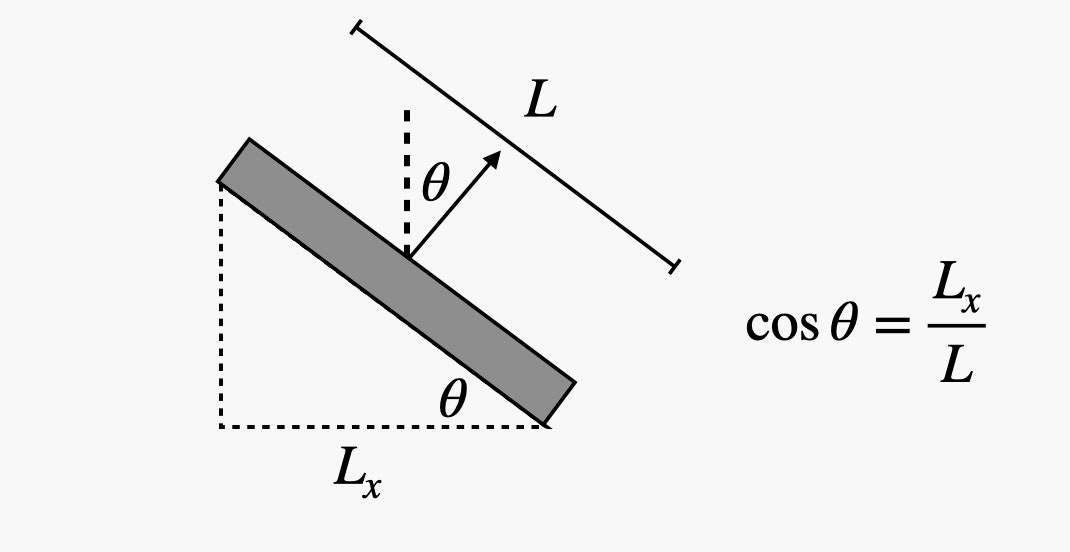
To perform the required calculations, we use the cosine. The following equation for motion with constant acceleration will help us.

The start and end positions are zero (this is the surface). Here is an expression to help determine the time.

If we use y0 with a distance of 6.4 m (which is realistic), we have to use the quadratic equation. It is not so difficult. But we can also use time in the horizontal movement of the descent vehicle. Here is the equation of horizontal motion.
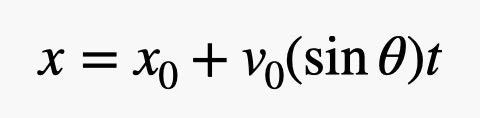
The speed depends on the sine of the angle. Now you can just leave x0 at zero and replace time with the above expression. As a result, we get this.
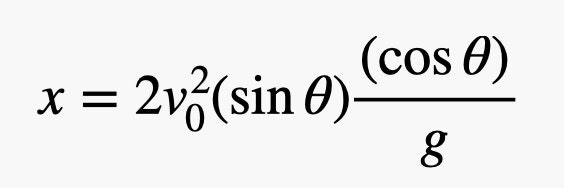
Substituting our values, we find that the distance the platform has moved away is 17.6 meters. But no, this is not at all the case. We know this from the photos published by NASA. According to the images, the platform landed at a distance of about a kilometer from the rover. We change the condition of the problem.
In order not to pose a danger to the rover, the platform should fly away at a distance of about 1 km. Descent speed - 8.2 m / s with an angle of inclination of about 52 degrees. How high will the platform rise before the engines shut off? We use this formula.

Now we use the time to solve the next equation.

If we carry out calculations, it turns out that the indicator for a vertical start is 43 km. Why is that? The point is that the platform sped up when the engines were launched.
Let's try to do some calculations in Python. The calculation consists of two parts. First, for a certain time, the rocket will fly at a constant acceleration of 52 degrees. It is only necessary to select the time and acceleration, and then calculate the fall of the body on the surface of Mars. Here is the code for the program that does all the calculations.
GlowScript 3.0 VPython
v0=8.2
g=3.7
theta=52*pi/180
x=1000
y0=.5*g*(x/(v0*sin(theta)))**2-x*cos(theta)/sin(theta)
tgraph=graph(width=550, height=350, xtitle="x-position [m]", ytitle="yx-Position [m]", title="Trajectory of Descent Stage Fly Away")
f1=gcurve(color=color.blue)
#starting position
x=0
y=6.4
#rocket firing time
tf=7
#rocket acceleration
a=6
#initial velocity
vy=v0*cos(theta)
vx=v0*sin(theta)
#time
t=0
dt=0.01
#rockets firing
while t<tf:
vy=vy+a*cos(theta)*dt
vx=vx+a*sin(theta)*dt
y=y+vy*dt
x=x+vx*dt
t=t+dt
f1.plot(x,y)
#to record max height
ymax=0
#projectile motion
while y>=0:
vy=vy-g*dt
y=y+vy*dt
x=x+vx*dt
if vy<0.1:
ymax=y
t=t+dt
f1.plot(x,y)
print("Descent Range = ",x," m")
print("Maximum Altitude = ",ymax," m")
print("Fly Away Time = ",t, " seconds")
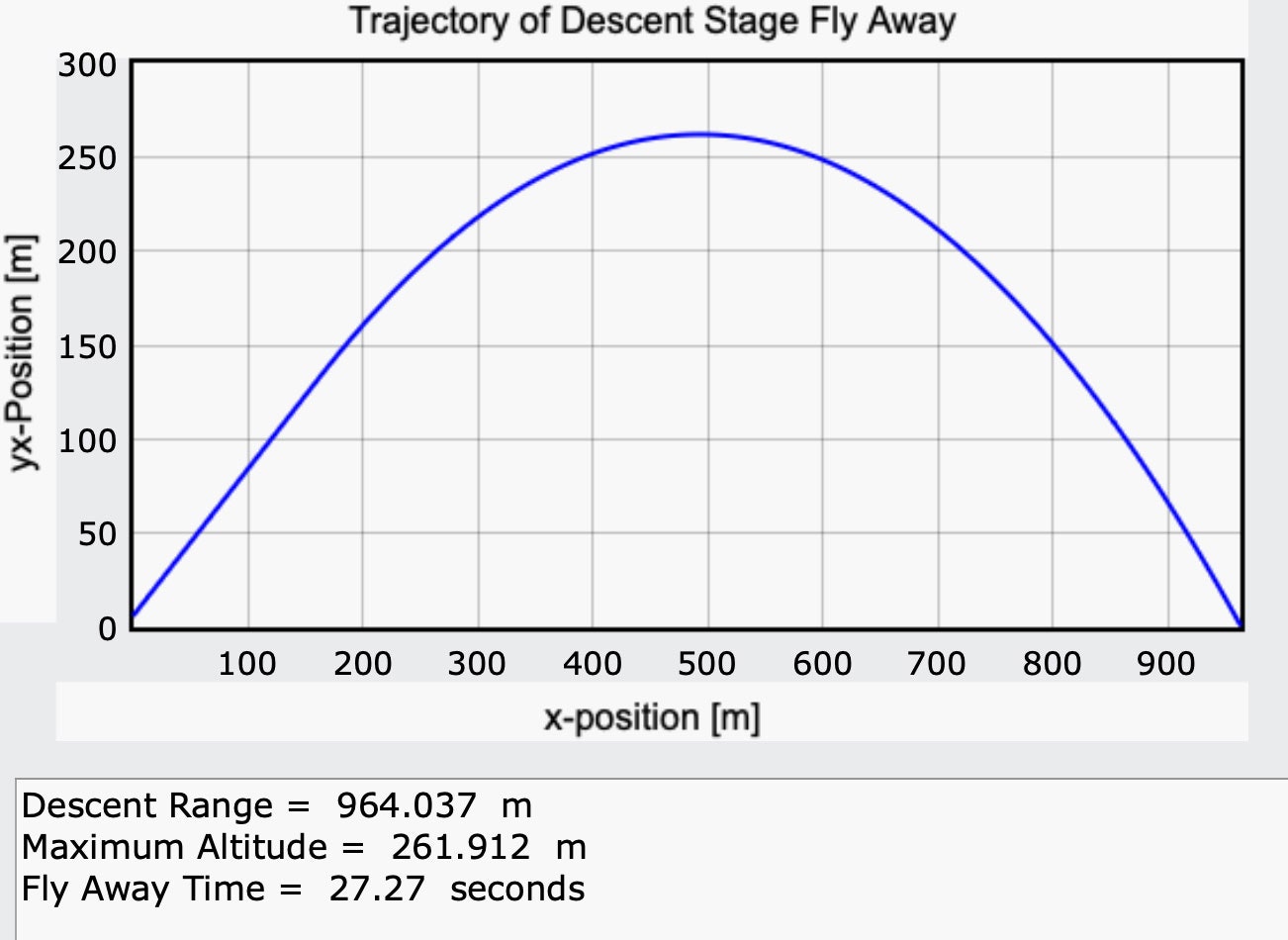
For calculations, we take the platform acceleration of 6 m / s 2 and the operating time of the engines in 7 seconds. And we get already a normal value of 964 meters, which is already very similar to the truth. Finally.
