Introductory article on implementing Feature Target Encoding

I recently did a project in which the target variable was multi-class, so I was looking for suitable ways to encode categorical features. I found many articles listing the benefits of coding through the average of the target variable over other methods, and how to accomplish this task in two lines of code using the category_encoders library   . However, to my surprise, I found that no article demonstrated this method for a multiclass target variable. I looked through the category_encoders documentation and realized that the library only works for binary or real variables, looked at the original work by  Daniele Micci-Barreca, which introduced mean target encoding and also did not find anything sensible. 

In this article, I will give an overview of the document that describes the target encoding and show with an example how the target encoding works for binary problems.

Theory

So: if you are asked "0/1", "clicked / not clicked" or "cat / dog", then your classification problem is binary; if you want to answer "red or green or blue, but maybe yellow" or "sedan versus hatchback and all versus SUV," then the problem is in several classes.

Here's what the categorical goal article I mentioned above has to say:

The result of any observation can be displayed through an estimate of the probability of the target variable.

, , .

.

, .

.  0, 1. P (Y = 1 | X = X_i), ..:

n(Y) - 1 ,

n(i) - i- ,

n(iY) - 1 i- . 

, 1 i- , - 1 . λ - , 0 1, n(i), .

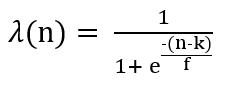
TargetEncoder category_encoders, k - min_sample_leaf, f - .

, , , .  , , , (. . Y).  .

.  .  , . , , , .  .

, .

.

, 1, «»?

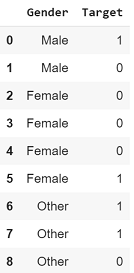
: 1/2 = 0,5.

, , Target 1, «»?

: 1/4 = 0,25.

?

, «Female» 0,25, .  , 4/9 = 0,4.

, «» , , .

min_sample_leaf, k = 1 , f = 1,

«Male», n = 2;

λ(‘Male’)=1/(1+exp(-(2–1)/1))=0.73    # Weight Factor for 'Male'

Target Statistic=(Weight Factor * Probability of 1 for Males)

       + ((1-Weight Factor) * Probability of 1 Overall)S(‘Male’)= (0.73 * 0.5) + ((1–0.73) * 0.4) = 0.485
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, «Female» , n = 4;

λ(‘Female’)=1/(1+exp(-(4–1)/1))=0.95 #Weight Factor for 'Female'

Target Statistic=(Weight Factor * Probability of 1 for Females)

    + ((1-Weight Factor) * Probability of 1 Overall)S(‘Female’)= (0.95 * 0.25) + ((1–0.95) * 0.4) = 0.259
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

, , λ , .  4 «Female», 2 «Male».  0,95 0,73.

, «Male» 0,485 , «Female» 0,259.  «».

!  !

?

, , category_encoders:

!pip install category_encoders

import category_encoders as ce 

x=['Male','Male','Female','Female','Female','Female','Other','Other','Other']

y=[1,0,0,0,0,1,1,1,0]

print(ce.TargetEncoder().fit_transform(x,y))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
    

TargetEncoder category_encoders.  , .  , .

  , . 

!